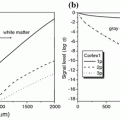
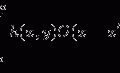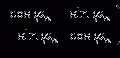Fig. 2.1
Scattered intensity distribution around a dielectric particle (n = 1.51) of different radii: a a = 0.05 µm, and b a = 1 µm. The solid and dotted curves correspond to the S and P polarization states of the illumination wave (λ = 632.8 nm), respectively
Biological tissue is usually composed of small scatterers such as bacteria, viruses, malignant cells and so on. The size of these scatterers varies from 0.1 μm to a few micrometers [1, 2]. Therefore, the dominant scattering effect caused by these scatterers is Mie scattering rather than Rayleigh scattering. The Mie scattering theory [3–5] provides an important physical foundation of the Monte Carlo simulation for optical microscopic imaging through a tissue-like turbid medium consisting of scattering particles such as cells and nuclei. However, these small scattering particles are sometimes aggregated because of their biological and chemical functions [6, 7]. A fractal aggregate is a medium with an ensemble of small scattering particles which, due to the physical mechanisms of aggregation , lead to a fractal structure, i.e., a scale-invariant structure [8]. Recently, an effective Mie scattering theory has been developed to derive the scattering property of a single spherical aggregate [9]. In this method, scattering properties of a single spherical aggregate consisting of Mie scatterers is derived from the Monte Carlo simulation. Therefore, such a method will be introduced in Chap. 3 after the introduction of the Monte Carlo simulation.
2.2 Mie Scattering Theory
There are many methods to describe the interaction of light and matter. Mie scattering theory describes scattering of a plane wave by a small particle with an insight into the collision process between photons and scattering particles. The scattering property of a scatterer forms a physical base of a scattering medium or a turbid medium which consists of a large number of scattering particles randomly dispersed.
As shown in Fig. 2.2, when a beam of light with specified characteristics illuminates a given small particle, the amount of the light scattered by the particle along with its angular distribution depends directly on the characteristics of the particle, including its shape, size, and the materials of which it is composed. The physics and mathematics for the interaction of an electromagnetic wave with a sphere is complicated and cumbersome and has been well documented in a number of classic textbooks [3–5]. Therefore, only the Mie theory formulations of scattering parameters including the scattering coefficients, scattering cress-section, anisotropy value, scattering efficiency, and scattering mean free path length, which are needed to calculate the scattering parameters, are presented in this section.
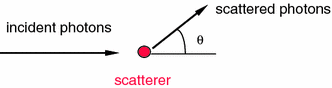

Fig. 2.2
An incident plane wave is scattered by a small particle. The scattered photons propagate at angle θ with respect to the incident direction
2.2.1 Scattering Coefficients of a Spherical Particle
For a spherical particle of a given particle size, the size parameter, x, and the relative refractive index, m, are given by [3]
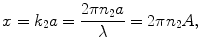
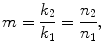
where k is the wave vector, a is the radius of the spherical particle, n is the refractive index and 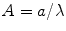 is the relative particle size. Here the subscripts 1 and 2 represent the surrounding medium and the scattering particle, respectively.
is the relative particle size. Here the subscripts 1 and 2 represent the surrounding medium and the scattering particle, respectively.
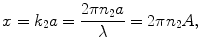
(2.1)
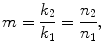
(2.2)
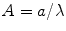 is the relative particle size. Here the subscripts 1 and 2 represent the surrounding medium and the scattering particle, respectively.
is the relative particle size. Here the subscripts 1 and 2 represent the surrounding medium and the scattering particle, respectively.The scattering coefficients given by the Mie theory [3], a i and b i , which represent the weighting parameters for the electromagnetic normal modes scattered by a spherical particle defined by (2.1), are given by
![$$a_{i} = \frac{{\mu_{1} m^{2} j_{i} \left( {mx} \right)\left[ {xj_{i} \left( x \right)} \right]^{{\prime }} \,-\, \mu_{2} j_{i} \left( x \right)\left[ {mxj_{i} \left( {mx} \right)} \right]^{{\prime }} }}{{\mu_{1} m^{2} j_{i} \left( {mx} \right)\left[ {xh_{i}^{\left( 1 \right)} \left( x \right)} \right]^{{\prime }} \,-\, \mu_{2} h_{i}^{\left( 1 \right)} \left( x \right)\left[ {mxj_{i} \left( {mx} \right)} \right]^{{\prime }} }},$$](/wp-content/uploads/2016/09/A71851_1_En_2_Chapter_Equ3.gif)
and
![$$b_{i} = \frac{{\mu_{2} j_{i} \left( {mx} \right)\left[ {xj_{i} \left( x \right)} \right]^{{\prime }}\, -\, \mu_{1} j_{i} \left( x \right)\left[ {mxj_{i} \left( {mx} \right)} \right]^{{\prime }} }}{{\mu_{2} j_{i} \left( {mx} \right)\left[ {xh_{i}^{\left( 1 \right)} \left( x \right)} \right]^{{\prime }}\, -\, \mu_{1} h_{i}^{\left( 1 \right)} \left( x \right)\left[ {mxj_{i} \left( {mx} \right)} \right]^{{\prime }} }},$$](/wp-content/uploads/2016/09/A71851_1_En_2_Chapter_Equ4.gif)
respectively, where the prime indicates differentiation with respect to the argument in the parenthesis. Here j i (mx) and 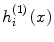 are the spherical Bessel functions of the first and third kind, respectively, given by
are the spherical Bessel functions of the first and third kind, respectively, given by
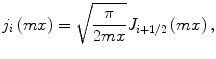
and
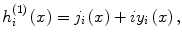
where y i (x) is a spherical Bessel function of the second kind
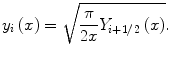
![$$a_{i} = \frac{{\mu_{1} m^{2} j_{i} \left( {mx} \right)\left[ {xj_{i} \left( x \right)} \right]^{{\prime }} \,-\, \mu_{2} j_{i} \left( x \right)\left[ {mxj_{i} \left( {mx} \right)} \right]^{{\prime }} }}{{\mu_{1} m^{2} j_{i} \left( {mx} \right)\left[ {xh_{i}^{\left( 1 \right)} \left( x \right)} \right]^{{\prime }} \,-\, \mu_{2} h_{i}^{\left( 1 \right)} \left( x \right)\left[ {mxj_{i} \left( {mx} \right)} \right]^{{\prime }} }},$$](/wp-content/uploads/2016/09/A71851_1_En_2_Chapter_Equ3.gif)
(2.3)
![$$b_{i} = \frac{{\mu_{2} j_{i} \left( {mx} \right)\left[ {xj_{i} \left( x \right)} \right]^{{\prime }}\, -\, \mu_{1} j_{i} \left( x \right)\left[ {mxj_{i} \left( {mx} \right)} \right]^{{\prime }} }}{{\mu_{2} j_{i} \left( {mx} \right)\left[ {xh_{i}^{\left( 1 \right)} \left( x \right)} \right]^{{\prime }}\, -\, \mu_{1} h_{i}^{\left( 1 \right)} \left( x \right)\left[ {mxj_{i} \left( {mx} \right)} \right]^{{\prime }} }},$$](/wp-content/uploads/2016/09/A71851_1_En_2_Chapter_Equ4.gif)
(2.4)
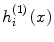 are the spherical Bessel functions of the first and third kind, respectively, given by
are the spherical Bessel functions of the first and third kind, respectively, given by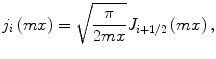
(2.5)
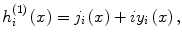
(2.6)
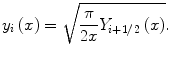
(2.7)
Here i denotes the i-th mode of an electromagnetic wave. In the above definition, 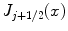 and
and 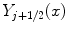 are Bessel functions of the first and second kind, respectively. The detail of Bessel functions can be found from the standard textbook [10].
are Bessel functions of the first and second kind, respectively. The detail of Bessel functions can be found from the standard textbook [10].
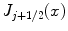 and
and 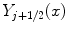 are Bessel functions of the first and second kind, respectively. The detail of Bessel functions can be found from the standard textbook [10].
are Bessel functions of the first and second kind, respectively. The detail of Bessel functions can be found from the standard textbook [10].2.2.2 Scattering Cross-Section and Anisotropy Value
The scattering cross-section , σ s, represents the cross-sectional area within which a scattering particle can interact with the illumination light. The scattering cross-section, σ s, for a spherical particle, defined by (2.1), is given by [3]
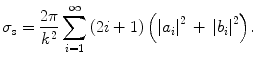
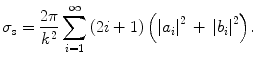
(2.8)
The anisotropy value (or the asymmetry parameter), 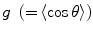 , which defines the averaged directional change of the scattered light, is given by [3]
, which defines the averaged directional change of the scattered light, is given by [3]
![$$gQ_{\text{s}} = \frac{4}{{x^{2} }}\left[ {\sum\limits_{i = 1}^{\infty } {\frac{{i\left( {i + 2} \right)}}{i + 1} {Re} \left\{ {a_{i} a_{i + 1}^{*} + b_{i} b_{i + 1}^{*} } \right\}} } \right.\;\left. { + \sum\limits_{i = 1}^{\infty } {\frac{2i + 1}{{i\left( {i + 1} \right)}}} {Re} \left\{ {a_{i} b_{i}^{*} } \right\}} \right],$$](/wp-content/uploads/2016/09/A71851_1_En_2_Chapter_Equ9.gif)
where Q s is the scattering efficiency defined as
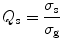
and σ g is the geometric cross-sectional area projected onto a plane perpendicular to the incident beam (i.e., 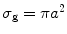 for a spherical particle). It should be noted that the anisotropy value, g, ranges from 0 to 1, where g = 0 represents isotropic scattering and g = 1 represents only forward scattering .
for a spherical particle). It should be noted that the anisotropy value, g, ranges from 0 to 1, where g = 0 represents isotropic scattering and g = 1 represents only forward scattering .
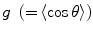 , which defines the averaged directional change of the scattered light, is given by [3]
, which defines the averaged directional change of the scattered light, is given by [3]![$$gQ_{\text{s}} = \frac{4}{{x^{2} }}\left[ {\sum\limits_{i = 1}^{\infty } {\frac{{i\left( {i + 2} \right)}}{i + 1} {Re} \left\{ {a_{i} a_{i + 1}^{*} + b_{i} b_{i + 1}^{*} } \right\}} } \right.\;\left. { + \sum\limits_{i = 1}^{\infty } {\frac{2i + 1}{{i\left( {i + 1} \right)}}} {Re} \left\{ {a_{i} b_{i}^{*} } \right\}} \right],$$](/wp-content/uploads/2016/09/A71851_1_En_2_Chapter_Equ9.gif)
(2.9)
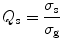
(2.10)
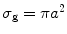 for a spherical particle). It should be noted that the anisotropy value, g, ranges from 0 to 1, where g = 0 represents isotropic scattering and g = 1 represents only forward scattering .
for a spherical particle). It should be noted that the anisotropy value, g, ranges from 0 to 1, where g = 0 represents isotropic scattering and g = 1 represents only forward scattering .Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree