SFUD, IMPT, and Plan Robustness

Fig. 12.1

Stages of the planning process for PBS: (a) Planning CT, (b) All deliverable BPs, (c) Selected and pre-weighted BPs, (d) Optimized BPs

Figure 12.1b shows an initial estimation of the possible positions of all Bragg peaks (red crosses) that can be delivered from this field direction. These are determined by three main parameters. The maximum field size for the scanned beams (scan range), which determines the maximum extent of the delivered BP’s orthogonal to the field direction (top and bottom in the figure), the selected separation of pencil beams in the scanning directions (in this case 4 mm), and the energy of each “layer” of Bragg peaks along the beam direction. Note that as only one slice through the patient is shown here, the second scanning direction will be in and out of the plane of this image, and thus we would have a similar pattern of BP positions in the CT slices above and below that shown (cranial and caudal directions in the patient).

The depth of BPs along the field direction is determined by the energy of each layer of BPs, with those of higher energy being deeper in the patient in relation to the incident field direction than those of lower energy. Their separation is thus determined by a discretization of the deliverable energies by the treatment machine. In the case shown here, this is determined by the available “tunes” of the PSI gantry 2, where each tune corresponds to a beam line setting through the gantry appropriate for a particular energy of protons. For our machine, these have been selected to provide energy steps equivalent to 2.5 mm shifts of the Bragg peak range in water. However, as the Bragg peak width increases as a function of increasing depth (due to a statistical broadening of the energy spectrum known as range straggling), this 2.5 mm separation is unnecessary for deeper energies. In our current implementation therefore, for ranges in water above 13 cm, only every second Bragg peak is considered by the TPS, thus resulting in a water equivalent separation of BPs of 5 mm in depth. Below 13 cm, every available proton energy is considered, thus resulting in a water equivalent separation of 2.5 mm. Note that this approach is specific to the planning system at our institute, and other energy/range separations are of course possible. For instance, many commercial systems use constant energy, rather than range, steps of 3–5 MeV, which results in a naturally smoother separation of Bragg peaks as a function of depth.

The observant reader will however have noticed something about the separation of BPs along the beam direction in the patient geometry shown in Fig. 12.1b. That is, the BPs are not regularly spaced, despite the fact that, in water, their ranges would be spaced at 5 or 2.5 mm intervals. This is of course due to the density heterogeneities in the patient. As can be seen in the underlying CT data, there are large density variations within the patient, ranging from the bones of the skull and skull base, through the gray and less dense soft tissues of the brain to the air cavities in the inner ears and nasal cavities. Thus, although the BPs are regularly spaced in depth if applied in water, this cannot be the case in the patient, with the protons clearly penetrating deeper into the patient where the densities are low (e.g., the air cavities) or less far where they are high (e.g., in the bones). Therefore, the actual separations in the patient will be much smaller in bone than in air, where due to minimal energy loss, the BPs shoot through to the other side. Only in the brain and other soft tissues therefore are the BP separations in the patient close to those for water.

Figure 12.1b shows all possible BPs that could be delivered from the defined field direction with the parameters of the machine as they have been defined. However, it is hopefully clear that this distribution of BPs is less than optimal, or at least not necessary, for conforming the dose to the target volume (yellow contour). For instance, it is obvious that any BPs delivered outside the target are unlikely to contribute any useful dose to the target and will only add to the doses delivered to the surrounding normal tissues. As such, an obvious next step is to select just those BPs that contribute dose to the target volume, the result of which is shown in Fig. 12.1c. These consist of all BPs within the target contour and also those up to 5 mm outside of the contour. Although these additional “external” BPs may not be absolutely necessary, when using BP grids with a regular spacing in all directions, as is the case here, BPs with distances from the target surface up to the inter-pencil beam spacing distance are required in order to ensure full target coverage.

In Fig. 12.1c, each of the selected BPs have also now been assigned a fluence (weight), as indicated with the differing colors of the crosses. In this case, this is a pre-weighting process before the final optimization process described next. In the pre-weighting strategy shown here, BP weights vary only along the beam direction and have been weighted such that the effective dose delivered by each line of BPs is similar to that of a spread-out Bragg peak (SOBP) as used for modulating depth doses in passive scattering [34]. Thus, the fluences vary identically along each line of BPs along the field direction, with the highest weights assigned to the most distal BP and then decreasing toward the proximal part of the target. Note that this decrease in weight to form a flat SOBP is very rapid, and therefore the BP weights in Fig. 12.1c have been displayed using an exponentially scaled color scale (shown on the right).

Figure 12.2a shows the dose distribution for this slice resulting from calculating the dose contribution from each pencil beam positioned and weighted as shown in Fig. 12.1c (plus all the other pencil beams of the field in planes parallel to that displayed). Unfortunately, although we have conformation of the dose to the target, dose homogeneity is not very good, particularly at the edge of the volume. This is invariably the case for irregular-shaped targets in inhomogenous surroundings, where there is essentially a loss of proton “equilibrium” at the edge of the target, leading to underdosage in these areas. For this reason, an optimization step is required which, based on the dose differences local to each pencil beam, increases or decreases its fluence. As is common with optimization in radiotherapy planning applications, this step is based on a gradient-based, iterative procedure which will not be described in detail here, but the details of which can be found in [3, 4, 40].

Fig. 12.2

Unoptimized (a) and optimized (b) dose distributions for the same case and slice as in Fig. 12.1

The result of the optimization step (after 60 iterations) is shown in Figs. 12.1d and 12.2b. Figure 12.1d shows the resultant BP fluences after the optimization step, while Fig. 12.2b shows the resultant dose distribution. By comparing the two dose distributions in Fig. 12.2, the result of the optimization step is clear. The resulting dose across the target volume is now much more homogenous, and the 95 % isodose contour (the blue area in the figure) almost exactly follows the target contour, indicating the level of conformation achievable with even a single field for PBS proton therapy.

Before moving on, it is worth saying a few words about the pre-weighting step described above. In principle, given a perfect optimization engine, this step should be unnecessary, with the optimizer anyway finding the optimal solution without needing to pre-weight the pencil beams. However, as will be discussed in more detail below, there are in fact many different solutions to the optimization problem for PBS proton therapy (see, e.g., [39]) which result in remarkably similar dose distributions. The pre-weighting step described above essentially “pushes” the solution in a particular direction (one that is the closest to the SOBP starting condition) and also makes the job of the optimizer somewhat easier and quicker. This issue won’t be discussed any more here, but the interested reader is referred to the work by Albertini et al. [3, 4]) for a study into the importance of pre-weighting for PBS treatment plans.

12.2.2 Combining Fields: Single-Field, Uniform Dose (SFUD), and Intensity-Modulated Proton Therapy (IMPT)

In the previous section, we described the process of constructing and optimizing a single field of a PBS treatment. In this and the next section, we will expand on this and look into different ways of combining PBS fields into clinically relevant treatment plans.

The process described above results in a more or less homogenous dose across the target volume, as seen in Fig. 12.2b. As such, if there are no other requirements or constraints for the treatment, such a single field could, in principle, be enough. Indeed, in some treatments, this may well be the case, as for example, in the irradiation of the whole cranial-spinal axis for the treatment of medulloblastoma [77]. However, in general, and as in conventional therapy with photons, typical PBS treatments consist of multiple fields, incident from different directions.

There are two main approaches to combining fields for PBS proton therapy, which have been defined as single-field uniform dose (SFUD) and intensity-modulated proton therapy (IMPT) [40–43].

SFUD is perhaps the simplest, and consists of the simple, linear addition of multiple fields constructed exactly as described in the previous section. That is, pencil beam fluences are optimized for each field independently and with the sole goal of constructing a dose distribution across the target that is as homogeneous as possible. An example SFUD plan is shown in Fig. 12.3, with the dose distribution for the full plan shown in the center, together with the dose distributions for the individual fields. Note, however, when combining such fields together, different field weights can be assigned in order to adjust the contribution of each field to the target volume. Typically, such differential weighting of fields is done in order to either reduce the weight of fields which have a worse in-field dose homogeneity or in order to reduce the weight of fields which are passing through, or stopping against, critical structures. Indeed, in the SFUD plan shown in Fig. 12.3, the weight of the lateral field has been somewhat reduced such that it only delivers a quarter of the total dose to the target, as it is partially stopping against the brain stem. Such a field arrangement and field weighting have been standard practice in our clinic for the first series planning of skull base chordomas for many years [6] and were initially adopted in order to make the planned dose to the brain stem somewhat more robust to potential range uncertainties (see below). Typically, about 60 % of all delivered plans in our clinic are SFUD, with this mode of PBS delivery being selected wherever possible.

Fig. 12.3

Example fields (a–c) and full plan (d) for a SFUD treatment to a skull base chordoma

A variant of the SFUD approach is now also becoming more popular, which has been called single-field optimization or SFO. This is similar to SFUD in that the pencil beam fluences are optimized for each field individually, but the SFO approach also allows for constraints to be applied to neighboring critical structures during the optimization of each individual field. Although not applicable in all cases, it is an interesting and somewhat more flexible extension of the SFUD approach.

The second main method of combining plans is somewhat more complex but has the advantage of maximally exploiting the full flexibility of PBS. This is what is now universally called intensity-modulated proton therapy, or IMPT [40].

In contrast to the SFUD approach, IMPT simultaneously optimizes the fluences of all pencil beams from all fields contributing to the plan. As such, there is no guarantee that the individual fields will be homogenous across the target, as is the case for the SFUD approach. Indeed for most applications of IMPT, this will certainly not be the case. However, the optimization of all pencil beams from all fields in the same process allows for much more flexibility in constructing the total dose distribution. For instance, if for one field, the pencil beam weights need to be reduced in order to reduce the dose to a critical structure, the resulting “hole” of dose in the target can be compensated by pencil beams from other fields. Thus, although the individual fields may become very inhomogenous, the final dose across the target from all fields can still be homogenous. This is the power of IMPT. Indeed, this planning and delivery approach has been so-called as it is the proton equivalent of IMRT with photons, in which the fluences of the individual photon fields can also be highly inhomogenous (highly modulated) in order to be able to selectively avoid overdosing critical structures.

Figure 12.4 shows a four-field IMPT plan to the same patient as for the plan in Fig. 12.3. However, in addition to attempting to deliver a homogenous dose as possible to the target volume, constraints have also been defined for the brain stem and optical structures, to which the delivered doses are clearly reduced in the full plan (Fig. 12.4e). Also shown in the figure are the dose distributions for the individual fields making up this plan, and it is immediately evident that the forms of the individual fields are very different from those of the SFUD plan shown in Fig. 12.3. Each field is now highly inhomogenous, and for the fields which are passing directly through the brainstem, the reduction in the fluences of the pencil beams is clear.

Fig. 12.4

Example fields (a–d) and full plan (e) for an IMPT treatment to the same case as Fig. 12.3: Note the four fields all have small table kicks of 20–30° in the cranial direction

In summary, IMPT provides the automation and flexibility of IMRT with photons, allowing for both maximizing target coverage while also selectively sparing neighboring critical structures as required.

Before moving on, an important note should be made. As has been pointed out by Stephen Dowdell (private communication), the idea of separating SFUD and IMPT is, in some ways, a false classification. Indeed, SFUD can really be seen as a special case of IMPT, but which is performed in such a way that the in-field modulation is minimized, and IMPT planning, when performed with no additional constraints on critical structures and with the correct pre-weighting strategy, can approach the SFUD solution. As more and more challenging constraints are added to the problem though, more and more modulation of the fields will be required. Thus, there is actually a “spectrum” of solutions, from SFUD through to highly modulated IMPT plans which progress as a function of in-field modulation. Nevertheless, we have always found it useful in our clinic to separate out SFUD and IMPT planning, and most commercial treatment planning manufacturers now support both modes.

12.2.3 Plan Degeneracy and Multi Criteria Optimization

Optimization is a key element in the construction of fields and plans for PBS proton therapy, as outlined in the previous sections. However, “optimization” is really the wrong name for this process, as there is typically not one “optimal” result of this process, at least not if the planning goals are relatively simple (i.e., dose homogeneity across the target volume only). This has already been eluded to when discussing the pre-weighting step above. In fact, for simple planning goals, there will be very many solutions of pencil beam positions and weights that give very similar final dose distributions (see, e.g. [39]). In optimization terminology, this characteristic is known as “degeneracy” and is an important concept in any form of optimized treatment planning and delivery.

In one of the first papers on IMPT [40], the degeneracy of the IMPT planning problem was already evident. In that paper, four “flavors” of IMPT were proposed, namely, 2D, 2.5D, 3D, and distal edge tracking (DET). Briefly put, 2D IMPT assumed that the delivered pencil beams had a fixed and identical SOBP depth-dose distribution, and thus only 2D modulation of the fluences is possible (relative fluence weighting along the depth-dose distribution being fixed in order to deliver a constant SOBP), whereas 2.5D IMPT expanded this concept and assumed that although each modulated pencil beam has an SOBP depth-dose characteristic, the extent of the SOBP is defined on a pencil beam by pencil beam basis such that it is customized to the thickness of the target at every pencil beam position. 3D IMPT is defined as the completely free optimization and modulation of all pencil beams for all fields, without restricting the effective depth-dose characteristics to be that of a SOBP, while DET is a special case of 3D IMPT, where only pencil beams with Bragg peaks stopping on the distal edge of the target volume are considered (i.e., all Bragg peaks internal to the target volume are ignored). Although differences between these approaches in the normal tissue doses were observed when applied to an example case, to all intents and purposes, the final dose distributions were very similar. Thus, for target coverage alone, the four approaches can be considered to be “degenerate.”

Degeneracy can be both an advantage and disadvantage. On the negative side, with no other constraints, restrictions, and defined goals, there is little control of which solution the optimizer will reach. Hence our approach of pre-weighting the Bragg peaks before starting with the optimization process provides a good initial guess for the optimizer to move in the desired direction. As a gradient-based optimization approach is used [40], a solution will generally be found that is the closest to the starting conditions, and by pre-weighting with SOBP type weightings, this ensures that the resulting distribution of weights is uniformly distributed over the target. However, as discussed by Albertini et al. [3, 4], other pre-weighting scenarios can be used, for example, “inverse wedges” or even forcing the solution toward DET by simply setting the weights of all internal Bragg peaks to zero in the pre-weighting step.

On the positive side, however, degeneracy indicates that there is scope for posing more challenging problems to a PBS optimizer, or that, of the many similar “optimal” solutions possible, one or other may have some more desirable characteristics than others, and characteristics that may not necessarily be known a priori at the start of the planning process. This has led to the concept of Multiple Criteria Optimization (MCO), which is gaining much ground for both IMRT and IMPT optimization [12, 15–17].

Simply put, the MCO approach is a “smart” way of generating a set of plans which cover the spectrum of “optimal” solutions. Optimal may seem an odd term here, as we are deliberately talking about a set of plans rather than one. But when there are multiple, often conflicting criteria for a plan (e.g., achieving target coverage while also wishing to spare doses to one or more neighboring critical structures), there are indeed a “spectrum” of optimal solutions, which may vary as a function of how they ‘balance’ the conflicting requests (i.e., from maximizing target coverage and minimizing normal tissue sparing to minimizing target coverage in order to maximize the sparing of critical structures or even balancing target coverage against plan robustness [15]). Thus, the art of MCO is to find this spectrum of “optimal” plans (there are unfortunately many more suboptimal plans which don’t do either very well!) and be able to present them to the user in such a way that they can then browse through the possible solutions to pick the best. It seems to this author that such approaches are very likely the future for treatment planning for PBS proton therapy, although much development still needs to be done.

12.3 The Problem of Range Uncertainty

As discussed above, the main role of treatment planning for PBS proton therapy is to determine the best arrangement of fields, pencil beams, and weights for treating the tumor. However, the quality of such an arrangement can only be judged by assessing the resultant, 3D dose distribution produced by the TPS. Indeed, the fact that the treatment to be delivered can be estimated a priori and with a resolution of a few millimeters by computer simulation is one of the great strengths of radiotherapy, matched by few other therapeutic techniques apart from perhaps computer and robot assisted surgery. Nevertheless, it must always be remembered that such calculated dose distributions are just that – estimates. As such, in reality, the actual delivered dose distributions may vary from this calculated distribution to a greater or lesser amount. The sensitivity of a particular treatment plan to potential variations is referred to as “plan robustness.” In the second part of this chapter, we will concentrate on this important aspect, as it is generally expected that proton treatments are likely to be less robust than photon plans, and thus plan robustness, and its analysis, is an important issue for PBS proton treatments.

12.3.1 Sources of Delivery Uncertainties

There are many reasons why the delivered treatment will not be identical to the calculated dose distribution. The most obvious is the limitation of dose calculation engines by which the 3D dose distribution is calculated (and on which the optimization is based) or misalignments of the patient in relation to the beam on treatment days in relation to that assumed by the treatment planning system [5, 22, 42, 43, 63, 78, 79]. The effect of such errors will not be considered here however. Instead we will concentrate on what the author believes are the most important possible causes of differences between the calculated and delivered doses – range uncertainty and motion (discussed in the next section).

The main advantage of protons is their very well-defined range due to the Bragg peak, which provides (at least for pristine Bragg peaks) a sharp dose fall-off at the distal end. However, to best utilize this characteristic, the exact placement of such Bragg peaks in the patient needs to be known. And here lies a fundamental problem – the exact range of protons in the patient is subject to many uncertainties. This is due to many potential reasons, shown schematically in Fig. 12.5. In this figure, the sources of range uncertainties are ranked based on their estimated magnitude of effect, starting with the smallest at the top and the largest at the bottom. Thus, the clinical relevance of, e.g., CT artifacts can be more substantial than range uncertainties caused by increases in RBE in the Bragg peak. It must be pointed out however that this ranking is very subjective and other authors may rank these somewhat differently. Nevertheless, the figure gives an overview of the potential sources of range uncertainties in the patient and indicates that these are many. It also indicates whether the uncertainty is likely to be random in nature (i.e., will vary day to day over the course of fractionated treatments) or whether they are systematic (i.e., will be the same everyday). Systematic errors are, by their nature, the most worrying as, in contrast to random errors, they will not “wash out” with fractionation. As such, in the rest of this discussion, we will concentrate on the effects of systematic range uncertainties.

Fig. 12.5

Sources of range uncertainties. Σ systematic, σ random

12.3.2 CT Calibration

Most modern radiotherapy is based on CT. Similarly, the use of CT is essential for proton therapy as this is currently the only modality that provides the necessary information on tissue density to allow for accurate dose and range calculations in the patient geometry. Indeed, although the first patients were treated with protons already in the 1950s, its more widespread use had to wait until the invention of x-ray CT in the 1970s for this very reason. However, CT data actually provides a 3D map of x-ray attenuation relative to water, which first needs to be converted into proton stopping powers before it can be used for dose and range calculations in proton therapy.

There are a number of ways of doing this [29, 52, 83], but the most common is to use the stoichiometric method first proposed by Schneider et al. [74]. In brief, after a parameterization of the CT scanner through the use of tissue substitutes of known composition, a Hounsfield Unit (HU) to stopping power (SP) curve is then constructed for biological tissues based on their physical characteristics such as physical density and chemical composition. However, as typically only one CT is used for planning, and only one such calibration curve, any inaccuracies in the CT data or uncertainties in this calibration will propagate through the whole treatment (i.e., will propagate as classic systematic errors).

Although this approach is quite sophisticated and based on solid theoretical concepts, it can never be a perfectly exact process. For a start, the transformation from HU to SP is non-unique. That is, materials with the same HU can have quite different SP values and vice versa. For this reason, for clinical applications, a biologically specific curve is used. However, non-biological materials in the CT (such as the table top or fixation devices) will not necessarily lie on the same curve and, unless manually corrected, will lead to systematic range uncertainties. As an example, if we assume that the SP of a plastic table top of thickness 2 cm is overestimated by the calibration curve by just 5 % (i.e., the actual SP of the table lies just 5 % below the calibration curve), then this can already lead to a systematic range error of 1 mm. For this reason, non-biological materials in the CT are often outlined, and the HU or SP values within these structures manually changed in order to correct for these effects.

This is certainly not the end of the story however. Even for biological samples, any calibration process can never be perfectly accurate. After implementation of the stoichiometric approach at our institute, for instance, the accuracy of this approach was tested by Schaffner and Pedroni [72] on biological samples. These measurements showed that the uncertainty in the resultant calibration curve was about 1.5 % for soft tissues and 2 % in bone. Given that these measurements were performed under relatively ideal conditions (e.g., using simple phantom geometries), these uncertainties are in line with the generally accepted value usually assumed for treatment planning purposes, which is 3 to 3.5 % [5, 41, 49, 58]. Although such an accuracy is quite good, it should always be kept in mind that these nevertheless translate into absolute range errors of up to 3 mm for centrally placed cranial tumors and 6 mm for central pelvic tumors (i.e., prostate if being treated from the lateral aspect).

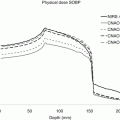
The effect of 3 % range uncertainties in a clinical setting is shown in Fig. 12.6 for SFUD and IMPT plans for a typical skull base chordoma. The top two figures show the dose distributions for the two plans, whereas the bottom two show so-called “error-bar” distributions [5] in which the color wash shows the potential magnitude of dose variations resulting from ±3 % range errors. For example, all areas displayed yellow in the bottom images correspond to voxels where the difference in dose resulting from +3 and −3 % range errors are between 10 and 15 % of the prescription dose (so about ±5–7.5 % about the nominal dose). This comparison shows that, although in the slices shown the largest error bars are for the SFUD plan, these are only in areas outside of the PTV margin and in areas of high-dose gradients, whereas for the IMPT plan, uncertainties of up to ±5–10 % can be seen within the CTV. Thus, for target coverage, the SFUD plan can be considered to be more robust than the IMPT plan.

Fig. 12.6

The potential effect of range uncertainties on SFUD and IMPT plans: (a, b) Nominal SFUD and IMPT plans, (c, d) “Error-bar” distributions for ±3 % range errors, where the colors now represent the width of possible doses at each point under these error conditions (max dose – min dose)

This example nicely shows the potential effects of the inevitable uncertainties in the CT calibration process for proton therapy and the quite different distributions of error magnitudes observed for the same case as a function of field arrangement and planning technique.

12.3.3 Range Extension Due to RBE

Relative biological effectiveness (RBE) is an important concept in particle therapy. It is a way of expressing the fact that the biological effectiveness of a given dose (deposited energy) can be different for different types of radiations. In comparison to photons, for example, the RBE for proton therapy is generally assumed to 1.1 globally (see, e.g., [57]). However, there is plenty of in vitro (cell-based) evidence that the RBE can also increase quite rapidly as a function of, in particular, decreasing proton energy [57]. As all protons in the Bragg peak have low energy, it is therefore expected that the RBE in this region could be considerably higher than 1.1, particularly in the distal fall-off region, where the average energy of the protons is the lowest. Such an increase can result in substantially higher biologically equivalent doses in the Bragg peak itself but also to a systematic “shift” of the distal fall-off to higher ranges. Thus, RBE uncertainty can also be considered a source of range uncertainty, with shifts in range of up to 3 mm being predicted in some conditions [14]. Such results have not been reproduced in in vivo studies, however, or necessarily for non-tumor cell lines [57], and therefore the clinical relevance of this is presently unclear [59]. Nevertheless, it is well worth keeping this potential effect in mind when planning proton treatments and is one of the reasons that most proton practitioners are extremely reluctant to “stop” single fields directly against critical structures.

12.3.4 CT Artifacts

After that short diversion into biology, let’s now return to CT data and an important issue which, thankfully, is not present in every patient.

There are a number of reasons why patients may have metal implants close to the treatment area. An obvious example (which is not too uncommon) is tooth fillings out of either amalgam or (much worse) gold. However, many patients may also present for proton therapy after substantial surgery in which bony structures (such as one or more vertebrae) need to be supported by titanium implants or where whole joints have been replaced with titanium prostheses (e.g., hip replacement surgery). Why can such implants effect proton range calculations? For two reasons: first, the implants themselves are not biological, and therefore won’t lie on the typical HU-SP calibration curve. Indeed, the density of these implants are so high that they will saturate CT scanners and will generally give a similar HU value whether titanium (SP ~3.1) or gold (SP ~10.0). So there is a problem with accurately calculating the correct energy loss in such structures, as it is impossible from the CT data sets to correctly predict their density or SP. In practice, this can be dealt with by identifying any metal structures and manually setting the SP for these to their true (usually measured) value. Second, the high density of these structures causes major problems for CT reconstruction algorithms, with complex or very dense structures creating large reconstruction artifacts.

An example of such artifacts is shown in Fig. 12.7a. This is a CT slice at the level of the upper thorax from a patient who has had previous surgery to remove a portion of the vertebrae, which was then subsequently supported by titanium rods fixed to the neighboring vertebrae through the use of titanium screws. Clear and coarse artifacts can be seen around the vertebrae area, with large areas of apparently very low HU values between the metal rods. These are not areas of low-density tissue, however, but rather reconstruction artifacts due to the metal. In fact, in these areas, there is actually a mixture of bone and soft tissue. Clearly, the calculation of proton range in these areas will always be wrong, simply because the CT data itself is already wrong.

Fig. 12.7

(a) An example CT slice at the level of the thorax for a patient with stabilizing metal (titanium) implants and (b) in the pelvis for a patient with a hip prosthesis

Due to the complexity of such artifacts, it is impossible to put a single value on the magnitude of the effect. However, Fig. 12.8 gives an idea of how such artifacts alone can affect proton range [1, 53].

Fig. 12.8

Range and dose perturbations due to metal induced CT reconstruction artefacts: (a) Dose planned and calculated on KVCT, (b) Dose recalculated on a MVCT of the same patient, (c) Profiles through the KVCT (blue) and MVCT (pink)

Figure 12.8a shows the dose distribution for a single SFUD field planned to a prostate carcinoma in which the field is passing directly through a titanium hip prosthesis, the CT slice of which is shown in Fig. 12.7b. The dose distribution has been planned on this KVCT data set in which the calibration curve has been modified such that the highest HU value is assigned to the stopping power of surgical grade titanium. As can be seen, although the prosthesis causes some dose irregularities in the distal fall-off of the field, the overall coverage and dose conformation is acceptable. In Fig. 12.8b, however, the same field has been recalculated on a MVCT data set of the same patient (this patient was actually treated using tomotherapy and has only been used here for simulation purposes). MVCT in this context has the advantage that reconstruction artifacts due to high-density implants are almost completely absent and is therefore a convenient imaging modality to use as a “ground truth” representation of the true anatomy of the patient. The difference in the dose distributions is obvious. When recalculated using artifact-free imaging, there is a clear undershoot of the field of 2–3 cm directly behind the metal implant in comparison to the dose planned on KVCT.

Only gold members can continue reading. Log In or Register to continue