SINUSES, NASAL CAVITY, AND CENTRAL SKULL BASE: SOLID MALIGNANT TUMORS
KEY POINTS
- Imaging is indispensable in differentiating routine sinonasal inflammatory disease from cancer and other aggressive pathology.
- Imaging can help avoid potential biopsy misadventure of a “mass” due to an encephalocele or excessively vascular lesion or one actually of blood vessel origin.
- Imaging spread patterns and occasionally lesion internal morphology can aid in the differential diagnosis of particular malignancies, but that is essentially a task for biopsy.
- Imaging is critical to planning the surgical approach to cancers and whether adjunctive radiation therapy will likely be needed in addition to other medical decisions.
INTRODUCTION
Etiology
Cancers of the nasal cavity and paranasal sinuses should be considered together. Many of these sinonasal malignancies are advanced at presentation. The precise site of origin may not be certain but usually becomes apparent on imaging.
Cancers of the nasal vestibule are generally considered separately from nasal tumors that develop posterior to the nasal aperture. Skin lines the nasal vestibule, so carcinomas arising in the nasal vestibule have a natural history similar to skin cancer.
Sinonasal adenocarcinoma has been linked to occupations associated with wood dust, boot making, shoe making, baking, and flour milling.1,2 Nickel refining workers have at least a 40-fold increased risk of developing squamous cell carcinoma of the nasal cavity. Squamous cell carcinoma (SCCA) may arise in a pre-existing inverted papilloma.
Prevalence and Epidemiology
Primary sinonasal and central skull base cancer is a relatively infrequent problem, with a yearly incidence estimated at one case for every 100,000 people. These malignancies occur in two men to each woman and typically appear after the age of 40 years. Some tissue types may appear before age 20 years, including those of minor salivary gland origin, lymphoma (Chapter 92), or olfactory neuroblastoma. Olfactory neuroblastoma (esthesioneuroblastoma) has a bimodal age distribution, peaking at ages 10 to 20 and 50 to 60 years.3 Primary carcinomas of the sphenoid and frontal sinuses are very rare.
The sinonasal region may be rarely the initial site of presentation due to a metastasis from a malignancy arising elsewhere, but this occurs much less frequently than in the orbit and mandible. Plasma cell dyscrasias and leukemia may involve the sinonasal region but only infrequently have such a presentation (Chapters 28 and 92). Chordomas arise from notochord remnants and are discussed in Chapter 34.
Clinical Presentation
Nasal vestibule cancers almost always present with a crusting, ulcerative, and/or bleeding mass at the entrance to the nose. On physical examination, there may be induration of the upper lip. Advanced lesions will erode through the nasal cartilages (Fig. 89.1).
Nasal cavity and paranasal sinus cancers in general often present with a history of chronic recurrent nasal obstruction and sinus problems. Symptoms are typically unilateral and consistent with chronic inflammation with discharge, obstruction, and intermittent epistaxis. The symptoms mimic those associated with nasal polyps; thus, cancer is often unanticipated at an early stage. The increased use of computed tomography (CT) for evaluating such complaints has probably resulted in somewhat earlier diagnosis than in the past. There may be an obvious mass bulging into the nasal vestibule. Nasolacrimal system obstruction causes epiphora and secondary dacryocystitis. Anterior skull base invasion may produce frontal headaches. Orbital invasion may cause proptosis and diplopia. Nasopharyngeal invasion may be submucosal and can produce symptoms related to eustachian tube obstruction. Spread to the masticator space causes trismus and headache secondary to invasion of the pterygoid muscles and the base of the skull. Paresthesias and/or pain in the V2 distribution are the most common symptom of cranial nerve involvement.
PATHOPHYSIOLOGY
Anatomy
The anatomic knowledge necessary for evaluating sinonasal cancer is fairly complex and must be understood in all three orthogonal planes. This anatomy is discussed in greater detail in Chapter 78. It is summarized here as it is related to the evaluation of malignant tumors. The specific regions of interest that must be understood in detail follow.
Nose and Nasal Vestibule
The nasal vestibule and related nasal cartilages from nares to the nasal cavity, including their relationship to the upper lip and orbital septum and fat plane deep to the superficial musculoaponeurotic system (SMAS), are important and sometimes underemphasized structures that are critical in evaluating tumors in this region.
The important related bones are the lacrimal, premaxilla, frontal process of the maxilla, and nasal bones.

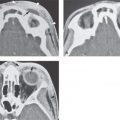
FIGURE 89.1. Magnetic resonance study of a patient with nasal vestibule cancer. A: Contrast-enhanced T1-weighted (T1W) image done with a small field of view receiver coil. The mucosal mass infiltrates the left nasal mucosa, circumferentially extending to involve the midline nasal septum (arrows). The nasal cartilage is spared (arrowhead). B: Another contrast-enhanced T1W image at a slightly different level. The anterior part of the tumor spreads to both sides of the nasal vestibule and along the midline nasal septum (arrows). The nasal cartilages (arrowheads) are not obviously involved posteriorly but could be involved anteriorly. C: Contrast-enhanced T1W image of a normal nasal vestibule and soft tissue structures of the nose for reference to (A) and (B). The nasal septum typically is of relatively low signal intensity (black arrow). The nasal mucosa enhances (black arrowhead). The junction of the nasal bone and cartilages is shown by the white arrowhead. The cartilage of the nose is shown by the white arrow.
Nasal Cavity
The nasal cavity and its relationships to the anterior nasal aperture where skin transitions to mucosa as well as where it ends at the posterior nasal aperture or choanae must be understood.
The hard palate forms the floor of the nasal cavity and its roof at the cribriform plate.
The nasal septum links the body of the sphenoid to the cribriform plate and the septal cartilage in the nasal vestibule anteriorly.
The turbinates, the floor of the ethmoid complex, and the medial maxilla and vertical palate of the palatine bone complete the important bony and other relationships of the nasal cavity.
Neurovascular Structures
The main neurovascular pedicle to the nasal cavity enters from the pterygopalatine fossa via the sphenopalatine foramen. The pterygopalatine fossa lies just inferior to the inferior orbital fissure, and the infraorbital nerve lies just superior to the fossa as it enters the foramen rotundum. The inferior orbital fissure and contiguous superior orbital fissures communicate with the middle cranial fossa. The pterygopalatine fossa region is perhaps the most important site with regard to medical decision making in sinonasal cancer. All of its bony and neurovascular relationships must be understood completely. It is here that perineural and/or perivascular spread of tumor will turn a lesion very quickly from resectable to likely unresectable for cure.
The olfactory nerves, as they penetrate the cribriform plate of the ethmoid bone, spread out over a dime-sized area of the upper one third of the septum and superior nasal turbinate. The perforations for the olfactory nerve fibers provide an avenue for tumor spread to the anterior cranial fossa.
The ethmoid roof has separate foramina and slits for passage of the anterior and posterior ethmoid neurovascular bundles. The latter typically lies 5 to 7 mm from the optic canal, usually at the anterior margin of the last ethmoid air cell. Both are consistently identified on CT and can help in orienting surgeons planning resections involving the anterior skull base.
Ethmoid Sinuses
The ethmoid sinuses consist of a labyrinth of air cells lying between the medial walls of the orbits and the lateral wall of the nasal cavity. The septae between the cavities are thin and offer almost no resistance to tumor spread. The ethmoid air cells are separated from the orbits by a very thin incomplete bony medial wall that is also easily penetrated by tumor. The posterior ethmoids are closely related to the optic canal and optic nerve. The anterior cells are covered laterally by the lacrimal bone. The roof of the ethmoid sinuses relates to the anterior cranial fossa as far posteriorly as the planum sphenoidale.
Sphenoid Sinus
The sphenoid sinus bears important relationships to the pituitary and optic chiasm that lie above, the cavernous sinuses laterally, the nasal cavity and ethmoid sinuses anteriorly, and the nasopharynx inferiorly. The sphenoid bone forms most of the floor of the middle cranial fossa. The basisphenoid forms the upper clivus posteriorly. Occasionally, there are gaps in the bony walls, and the mucous membrane may lie directly against the medial cavernous sinus dura.
Maxillary Sinus and Related Neurovascular Structures
The maxillary sinus has nasal (medial), orbital (roof), facial (anterior and lateral), and infratemporal (posterior and lateral) walls. These named relationships reflect important areas of potential cancer spread. The roof or orbital surface of the antrum contains the infraorbital canal and the related neurovascular bundle. The maxillary alveolus forms the floor of the antrum. The nasal wall has a primary and frequently accessory ostium. The junction of the orbital and nasal surfaces of the antrum forms the floor of the ethmoid sinus and is sometimes called the antroethmoidal septum.
The medial antral wall has a normal nonmineralized gap or fontanelle between the maxillary bone and the vertical plate of the palatine bone. This should not be mistaken for tumoral bone erosion.
The posterior and lateral antral wall borders the infratemporal fossa and the pterygopalatine fossa. The pterygopalatine fossa lies immediately behind the maxilla and is a pivotal point of distribution for nerves and blood vessels to the nasal cavity, sinuses, and infratemporal fossa.
The facial or anterior wall of the antrum is slightly concave and faces anteriorly and laterally. Before it emerges onto the face, the infraorbital nerve gives off an anterior superior alveolar branch that runs in the facial wall of the maxillary sinus to the incisor and canine teeth. Multiple other branches run in the fat pad deep to the SMAS.
The posterior superior alveolar nerve arises from V2 (the maxillary nerve) in the pterygopalatine fossa and runs downward and forward to pierce the infratemporal surface of the maxilla and descend under the mucosa of the maxillary sinus. This produces multiple small areas of dehiscence in the posterior antral wall.
Frontal Sinuses
The frontal sinuses lie between the outer and inner tables of the frontal bone. They connect to the middle meatus of the nasal cavity by either the frontal recess or ethmoid infundibulum. The posterior wall separating the frontal sinus from the anterior cranial fossa is thick in most patients.
Nasopharynx and Other Deep Soft Tissue Plane Relationships
Potential direct mucosal spread to the nasopharynx requires that its anatomy and variants be understood. The same is true of the soft tissue anatomy deep to the nasopharynx, which is another possible source of its involvement (Chapter 184).
Superficial Musculoaponeurotic System of the Face
The other important soft tissue relationships to the sinonasal region include those of the orbit, the infratemporal and temporal fossa, and the fat planes beyond the sinus walls and deep to the SMAS. A thorough knowledge of the SMAS itself and its relationship to the subcutaneous fat and skin is also essential (Fig. 78.25).
Lymphatics
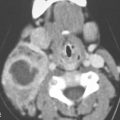
The nasal vestibule lymphatic trunks drain to the level 1 nodes. There is a risk for involvement of facial nodes, including the infraorbital, buccinator, and mandibular nodes of this group (Fig. 89.2). Metastasis to these facial nodes is more likely in recurrent disease (Fig. 89.2D). Parotid area lymph nodes are only rarely involved, but spread to facial nodes may herald an increased risk. The retrozygomatic node may be involved (Fig. 89.2A–C).
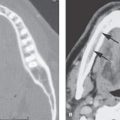
Nasal cavity capillary lymphatics are separated into the olfactory group and the respiratory group. According to Rouvière,4 they do not communicate. The lymphatics of the olfactory region of the nasal cavity run posteriorly to terminate in the retropharyngeal lymph nodes4 (Fig. 89.3). The lymphatics of the respiratory nasal cavity also terminate either at level 1 or level 2. The capillary lymphatic plexus of the nasal cavity is well developed over the middle and inferior turbinates, in the olfactory region, and around the choanae but is sparse over the lower septum.
Rouvière4 describes unusually delicate and sparse lymphatics in the frontal, ethmoid, and maxillary sinuses that connect with those of the nasal mucosa. This is borne out by clinical experience where even in primary sinus tumors that are frequently advanced, regional nodal metastases are uncommon. Lymph node metastases probably only occur once tumor has extended out of a sinus to areas containing capillary lymphatics, such as the nasopharynx, buccal mucosa, nasal cavity, and skin.
Pathophysiology and Patterns of Disease
Pathology
Since the nasal vestibule is covered by skin, the vast majority of the vestibule lesions are SCCAs (Figs. 21.12 and 21.12). The remainder is the occasional basal cell and adnexal structure–origin skin cancers. In the nasal cavity and paranasal sinuses, benign tumors frequently mimic malignancies. Some of these include inflammatory polyps, benign minor salivary epithelial neoplasms, and odontogenic tumors. Other processes such as giant cell granulomas and necrotizing sialometaplasia are less common mimics of cancer. More diffuse infiltrative but benign conditions frequently in the sinonasal region include Wegener granulomatosis (WG) and sarcoidosis.
SCCA accounts for about 85% to 90% of sinonasal malignancy.
A much smaller proportion of sinonasal cancers are minor salivary gland epithelial tumors (Figs. 22.24 and 89.4). Adenocarcinoma is the most common of this tissue of origin followed by adenoid cystic carcinoma and mucoepidermoid carcinoma (Fig. 89.4). When adenocarcinoma of the sinonasal tract is diagnosed, renal cell carcinoma and other distant primary sites must be kept in mind as a rare source of the cancer. Sinonasal undifferentiated cancer is the least well differentiated of the epithelial neoplasms that will be found in the sinonasal region (Figs. 23.13 and 89.5). This very aggressive malignancy will often invade the nasopharynx secondarily and at original presentation are sometimes mistaken for nasopharyngeal primary tumors.
Inverted papilloma, while usually benign, has malignant potential and must be treated like a low-grade malignancy (Figs. 23.3–23.5 and 89.6). Pathologically, it appears as a papilloma growing into rather than out from its stroma. Other terms have been used to describe these lesions, including schneiderian cell papilloma. This term and any others should be abandoned. Of all papillomas, 85% to 90% are histologically benign, but the remainder are associated with SCCA that may take an aggressive clinical course.

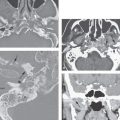
FIGURE 89.2. Cases of two patients demonstrating sinonasal cancer metastatic to facial lymph node groups. A–C: Patient 1. In (A), there is metastases to a buccal space node from an olfactory neuroblastoma (arrow). In (B), there is metastases to a node in the upper buccal space, sometimes called the retrozygomatic node (arrow). In (C), a sagittal view shows these two nodes as separate metastases. D: Patient 2. Olfactory neuroblastoma that metastasized to the mandibular node (arrow) of the facial group.
Sinonasal lymphoma is unusual and accounts for, 5% of cancers in this region. The relationship between T-cell angiocentric lymphoma and WG is discussed in Chapters 17, 27, and 92 (Figs. 17.2, 17.7, 27.1, 27.2, and 27.5). These lymphomas and WG manifest as nonhealing lesions that involve the nose, paranasal sinuses, and hard palate and progressively invade and destroy these and other contiguous structures. Sinonasal plasmacytoma and granulocytic sarcoma as localized manifestations of leukemia are also uncommon and are discussed in Chapters 28 and 92 (Figs. 28.2, 28.4, 92.3, and 92.4).
Sarcomas of soft tissue and bone may arise in the nasal cavity and paranasal sinuses. All are relatively rare. The more common include chondrosarcoma (Figs. 39.1 and 39.11), osteosarcoma (Figs. 38.8–38.10), and Ewing sarcoma. Rhabdomyosarcoma is the more common tumor in the pediatric age range. The various sarcomas are discussed in Section II, Chapters 35 through 39 (Figs. 35.12 and 89.7–89.9).
Olfactory neuroblastoma (esthesioneuroblastoma) is a malignant tumor of olfactory neuroepithelial origin. Modern immunohistochemical techniques now make histologic differentiation from sinonasal undifferentiated carcinoma, lymphoma, and meningioma simple (Figs. 30.1–30.6, 89.2, 89.10, and 89.11). Currently, there is a trend to consider this tumor as arising from the same cell line as those in the category of primitive neuroectodermal tumors. Other benign and malignant neural tumors occur in the nasal cavity (Fig. 30.11).
Malignant melanoma may arise primarily in the nasal cavity (Fig. 23.14). It is less common in the paranasal sinuses.
Metastases are uncommon but may present in the sinonasal region mimicking primary tumors (Fig. 89.12).
Patterns of Spread
General Principles
A complete understanding of the relationships between the facial skeleton, sinuses, nasal cavity, orbits, and brain is essential for the complex medical decision making required in the diagnosis and management of sinonasal cancer. The course of the maxillary, greater and lesser palatine, and infraorbital neurovascular bundles must be completely familiar to those interpreting these studies. The particularly critical relationships of the pterygopalatine fossa inferior orbital fissure, infratemporal fossa, sphenopalatine foramen, and foramen rotundum must be understood for proper interpretation of CT and magnetic resonance imaging (MRI) studies of sinonasal cancer patients.

FIGURE 89.3. Examples of sinus cancers metastatic to retropharyngeal nodes. A–C: Patient 1. In (A), there is an infiltrating cancer at the junction of the nasal vestibule and anterior nasal cavity (arrow) infiltrating deep to the superficial musculoaponeurotic system (arrowheads) and invading adjacent bone as well as spreading along the medial wall of the maxillary sinus into the posterior nasal cavity placing retropharyngeal nodes at risk (arrows). In (B), an abnormal retropharyngeal lymph node (arrow) contains an obvious low-density focus of metastatic disease (arrowhead). In (C), the patient also had metastatic disease to a level 2 lymph node (arrow) that was not palpable. D: Patient 2 treated for olfactory neuroblastoma. The only sight of treatment failure was in the left retropharyngeal lymph node (arrow); compare to the normal right retropharyngeal lymph node (arrowhead).
CT is best for rendering critical bone detail and MRI for marrow space invasion. Bone in the paranasal sinuses is predominantly cortical. In some locations, the apparent absence of bone on CT examinations may not be due to bone erosion or demineralization. The thin walls of the ethmoid air cells may “disappear” when the sinus contents are other than air. Broad portions of the maxillary sinus medial wall between the maxilla and vertical plate of the palatine bone are not ossified; this wall bulges easily and virtually always appears dehiscent.
Both contrast-enhanced MRI and contrast-enhanced CT are excellent for discriminating between tumor and obstructive changes in the sinuses; MRI is typically more definitive in this regard.
The nasal cycling may make the nasal turbinates appear much larger on one side of the nasal cavity. This can obscure tumor margins. The nasal mucosa can be treated with vasoconstrictors before MRI or CT studies to eliminate this problem.
The evaluation of perineural spread of tumor along the infraorbital nerves or within the pterygopalatine fossa and foramen rotundum region must take into account normal perineural enhancement that must not be mistaken for pathologic enhancement of the nerve. This normal perineural enhancement is most prominent in the foramen rotundum and foramen ovale.5 Careful side-to-side comparison of the trigeminal branches, greater and lesser palatine neural foramina, and pterygomaxillary fossa are necessary to detect early perineural involvement with tumor.



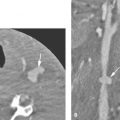
FIGURE 89.4. Examples of patients with perineural spread of sinonasal cancer. A–E: Patient 1 with adenoid cystic carcinoma of the left maxillary sinus extending into the left nasal cavity. In (A), T1-weighted images show the primary tumor (white arrowhead) in the inferior left maxillary sinus. It invades the greater palatine neurovascular bundle (white arrow). Extension along the posterior superior alveolar nerves is present (black arrowheads). Spread along V3 is also present (black arrow). In (B), a section somewhat more cephalad than that in (A) shows spread along the posterior sinus wall (white arrow) involving the posterior superior alveolar nerves (black arrowhead) compared to the normal nerves and vessels on the right side (white arrowhead). In (C), a section cephalad to the image in (B) shows invasion of the sphenopalatine foramen and pterygopalatine fossa (black arrow) with continued spread along the posterior sinus wall (arrowheads) and related posterior superior alveolar nerves. Compare to the normal pterygopalatine fossa on the right side (white arrow). In (D), there is a normal upper pterygopalatine fossa and inferior orbital fissure on the right for reference (white arrow). Perineural spread along V2 is shown by the black arrows to extend to the trigeminal cistern from perineural spread in the upper pterygopalatine fossa and inferior orbital fissure (black arrowhead). In (E), the T2-weighted image to correlate with (D) shows the normal inferior orbital fissure and pterygopalatine fossa region on the right (black arrow) compared to the infiltrated one on the left (white arrows) and continued spread along V2 (white arrowheads). F–I: Patient 2 with carcinoma arising in a benign mixed tumor of the hard palate and floor of the nose showing perineural spread. In (F), tumor infiltrates the posterior nasal cavity (arrowhead) and spreads to the pterygopalatine fossa and along the posterior sinus wall, infiltrating the posterior superior alveolar nerves (white arrows). Normal corresponding area is shown by the black arrowhead on the right. In (G), a section superior to that seen in (F) shows the infiltrating tumor entering the sphenopalatine foramen and infiltrating the pterygopalatine fossa (arrows) compared to the normal right side (white arrowhead). In (H), a coronal section to correlate with the previous two sections shows tumor that has spread to the upper posterior nasal cavity and into the pterygopalatine fossa by way of the sphenopalatine foramen (white arrows). In (I), the patient also had cervical metastatic disease that was not palpable. The upper left level 2 metastatic node (arrow) contains multiple small metastatic deposits (arrowheads).
Nasal Vestibule
Early nasal vestibule cancer may present as a mucosal ulceration. The lesions can grow through the nasal septum and/or invade the cartilage of the nose, growing through to the skin surface (Figs. 89.1 and 89.3). Inferiorly, the upper lip and columella may be involved with more advanced lesions growing into the gingivolabial sulcus; these lesions can invade the premaxilla or nasolacrimal canal. Posterior spread to the nasal cavity and along the floor of the orbit is possible. The infraorbital nerve may be invaded.
The facial and level 1 nodes are at risk. The lymph node spread is typically ipsilateral. Parotid lymph nodes are at very low risk of involvement.

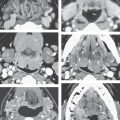
FIGURE 89.5. Computed tomography and magnetic resonance study of a patient with sinonasal undifferentiated cancer. A: The tumor in the high posterior nasal cavity infiltrates both pterygopalatine fossae from the sphenopalatine foramina (arrows). B: There is continued spread into the right cavernous sinus (arrows). C: Contrast-enhanced T1-weighted image to correlate with (A) and (B) showing the bilateral infiltrating tumor in the upper posterior nasal cavity infiltrating through both sphenopalatine foramina (arrows) and into the cavernous sinus (arrowhead) with sphenoid sinus changes due to tumor obstruction of the sinus ostium. D: T2-weighted image to correlate with (C) showing the signal intensity of the tumor (arrows) to be about the same as gray matter but much different from the obstructed sinus contents. Tumor is actually seen infiltrating into the ostia of both sphenoid sinuses as well as there being widespread involvement of the infratemporal fossa and fat pad posterior to the right maxillary sinus (arrow). The infiltrating tumor in the cavernous sinus is also visible (arrowheads).
Nasal Cavity
Nasal cavity spread patterns for the histologic variety of lesions possible are really about the same. The minor salivary gland tumors, especially adenoid cystic carcinoma, are more likely to show perineural spread (Figs. 89.3 and 89.4). Perineural spread is also more common in patients with recurrent tumors.
Cancers arising from the olfactory neuroepithelium soon invade the ethmoid sinuses, orbit, and anterior cranial fossa. The prototype of this lesion is olfactory neuroblastoma (Figs. 30.1–30.6, 89.10, and 89.11). The nasal septum and nasal bones may be destroyed. More lateral nasal cavity cancers invade the medial wall of the maxillary sinus, the ethmoid sinuses, the pterygopalatine fossa, and the orbit (Figs. 89.13–89.15). The anterior skull base is always at potential risk (Fig. 89.14).
Tumor invasion of the orbit is common at presentation and significantly alters morbidity and treatment plans (Figs. 30.1A, 30.4B, 89.13, and 89.15).
Secondary invasion of the nasopharynx and sphenoid sinus occurs in advanced nasal cavity cancers. The nasopharynx is invaded by mucosal spread through the posterior choana and is usually not amenable to surgical resection (Figs. 89.13 and 89.16).
Inverted papilloma is essentially a lesion of the lateral nasal wall. Other sites of origin are very unusual. The lesions are polypoid and more vascular than inflammatory polyps (Figs. 23.3–23.5 and 89.6). The attachment to the lateral nasal wall may be discrete compared to the bulk of the tumor. Adjacent maxillary and ethmoid sinus involvement is common. Spread to the orbit and anterior skull base is unusual, but it occurs. Bone erosion is common but may appear more as remodeling, sclerosis, and dehiscence than aggressive erosion (Figs. 23.3–23.5 and 89.6). Lymph node metastasis and perineural spread should only occur in a small subset of the 10% to 15% of cases with a complicating SCCA since the carcinomas are often only discovered within the confines of the papilloma as a histologic coincidental finding.

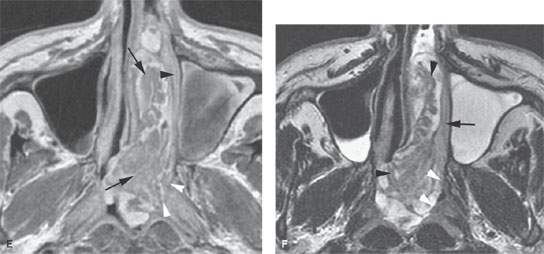
FIGURE 89.6. A patient with inverted papilloma. A: Computed tomography (CT) study shows a generalized opacification of the left nasal cavity and left maxillary sinus. There is bone loss as well as bone sclerosis present. The medial wall of the ethmoid complex is much thicker than usual (arrowhead), as is the bone of the antroethmoidal septum region (arrow). This finding is often present with inverted papilloma. B: T2-weighted (T2W) magnetic resonance (MR) image showing tumor that appears to be somewhat papillary growing all the way to the ethmoid roof (arrows). The thickened bone of the medial ethmoid wall can be anticipated (arrowhead) on the MR but not as definitively as on the CT in (A). C: Contrast-enhanced T1-weighted (T1W) image to compare with (A) and (B). The papillary and “fronding” nature of the mass as well as its extension to the ethmoid roof are noted again (white arrows). The thickened ethmoid bony wall can be anticipated as well as the thickened antroethmoidal septum (white arrowheads). The bulging margin of the obstructed maxillary sinus contents form an interface with the lateral aspect of the tumor (black arrowheads). D: Axial T2W images clearly show the frondlike nature of this papillary tumor (arrow) and clearly identify the interface between the tumor and obstructive sinus contents (arrowhead). E: Contrast-enhanced T1W image to compare with (D). The papillary mass fills the nasal cavity and extends into the nasopharynx (arrows). It does not appear to invade the nasopharyngeal wall but clearly apposes that mucosa (white arrowheads). The same is true of the nasal cavity mucosa (black arrowhead). F: T2W image for comparison with other axial images showing the frondlike nature of the tumor (arrowheads) and a possible more solid attachment of the tumor along the lateral nasal cavity wall (black arrow). The interface with the nasal pharyngeal wall is sharp (white arrowheads) and does not suggest invasion. Surgery showed the nasopharynx not to be invaded.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree