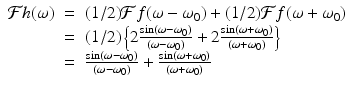(1)
Department of Mathematics and Statistics, Villanova University, Villanova, PA, USA
5.1 Definition and examples
For a given function f such that 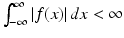 , the Fourier transform of f is defined, for each real number ω, by
, the Fourier transform of f is defined, for each real number ω, by
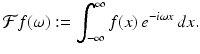
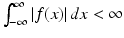 , the Fourier transform of f is defined, for each real number ω, by
, the Fourier transform of f is defined, for each real number ω, by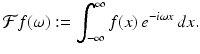
(5.1)
The idea behind this definition is that, for each value of ω, the value of 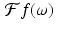 captures the component of f that has the frequency ω∕(2π) (and period 2π∕ω ).
captures the component of f that has the frequency ω∕(2π) (and period 2π∕ω ).
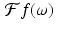 captures the component of f that has the frequency ω∕(2π) (and period 2π∕ω ).
captures the component of f that has the frequency ω∕(2π) (and period 2π∕ω ).Example 5.1.
The Fourier transform of a Gaussian. Let 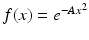 , for some positive constant A > 0. Then we have
, for some positive constant A > 0. Then we have
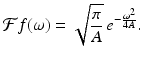
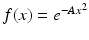 , for some positive constant A > 0. Then we have
, for some positive constant A > 0. Then we have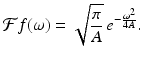
(5.2)
To prove this, we first need the following fact.
Lemma 5.2.
For A ≠ 0, we have 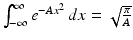 .
.
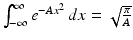 .
. Proof.
Squaring the integral, we get
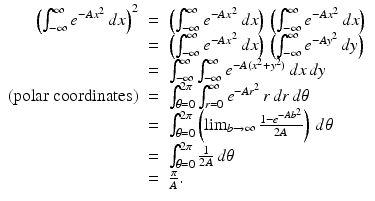 Taking square roots proves the lemma.
Taking square roots proves the lemma.
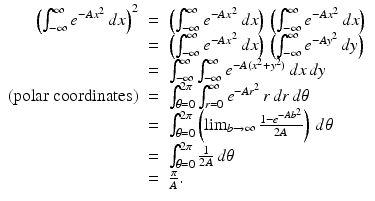
Now to compute the Fourier transform for this example. For each ω,
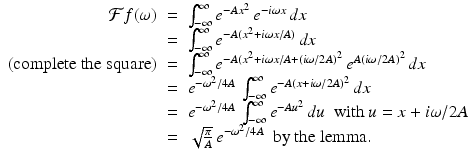 This establishes the result we were after. □
This establishes the result we were after. □
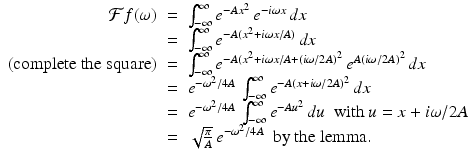
Observe that if we take 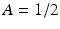 , then
, then 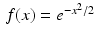 and
and 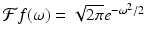 , a constant multiple of f itself. In the language of linear algebra, this function f is an eigenvector, or eigenfunction, of the Fourier transform.
, a constant multiple of f itself. In the language of linear algebra, this function f is an eigenvector, or eigenfunction, of the Fourier transform.
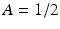 , then
, then 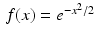 and
and 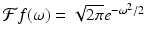 , a constant multiple of f itself. In the language of linear algebra, this function f is an eigenvector, or eigenfunction, of the Fourier transform.
, a constant multiple of f itself. In the language of linear algebra, this function f is an eigenvector, or eigenfunction, of the Fourier transform.Additional examples are considered in the exercises. Let us look at some basic properties of the Fourier transform.
5.2 Properties and applications
Additivity. Because the integral of a sum of functions is equal to the sum of the integrals of the functions separately, it follows that
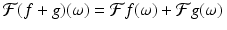
for all integrable functions f and g and every real number ω.
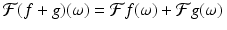
(5.3)
Constant multiples. Because the integral of c ⋅ f is equal to c times the integral of f, we see that
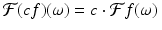
for all integrable functions f, all (complex) numbers c, and every real number ω.
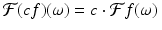
(5.4)
Proposition 5.3.
The Fourier transform acts as a linear transformation on the space of all absolutely integrable functions. That is, for two such functions f and g and any constants α and β, we get that
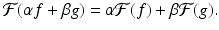
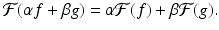
(5.5)
Shifting/translation. For an integrable function f and fixed real number α, let 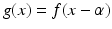 . (So the graph of g is the graph of f shifted or translated to the right by α units.) Then
. (So the graph of g is the graph of f shifted or translated to the right by α units.) Then
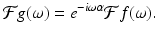
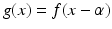 . (So the graph of g is the graph of f shifted or translated to the right by α units.) Then
. (So the graph of g is the graph of f shifted or translated to the right by α units.) Then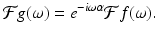
(5.6)
Proof.
For each ω, we get
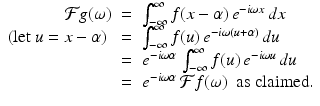
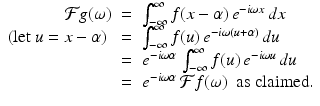
Since the graph of g is a simple translation of the graph of f, the magnitude of the component of g at any given frequency is the same as that of f. However, the components occur at different places in the two signals, so there is a phase shift or delay in the Fourier transform. Also, the fixed translation α encompasses more cycles of a wave at a higher frequency than at a lower one. (For instance, an interval of width α = 2π contains two cycles of the wave y = sin(2x), but only one cycle of the wave y = sin(x).) Therefore, the larger the value of α is relative to the wavelength 2π∕ω the larger will be the phase delay in the transform. That is, the phase delay in the transform is proportional to ω, which explains the factor of e −i ω α in the transform of the shifted function g.
Shifting/modulation. For a given function f and a fixed real number ω 0, let 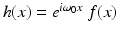 . (So h “modulates” f by multiplying f by a periodic function of a fixed frequency ω 0∕2π.) Then
. (So h “modulates” f by multiplying f by a periodic function of a fixed frequency ω 0∕2π.) Then
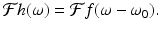
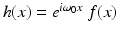 . (So h “modulates” f by multiplying f by a periodic function of a fixed frequency ω 0∕2π.) Then
. (So h “modulates” f by multiplying f by a periodic function of a fixed frequency ω 0∕2π.) Then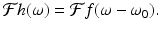
(5.7)
Proof.
For each ω, we get
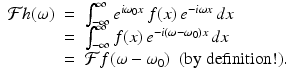
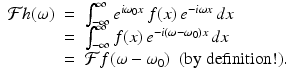
These two shifting properties show that a translation of f results in a modulation of  while a modulation of f produces a translation of
while a modulation of f produces a translation of 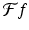 .
.
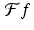 while a modulation of f produces a translation of
while a modulation of f produces a translation of 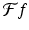 .
.Scaling. For a given function f and a fixed real number a ≠ 0, let ϕ(x) = f(ax). Then
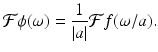
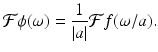
(5.8)
Proof.
Assume that a > 0 for now. For each ω, we get
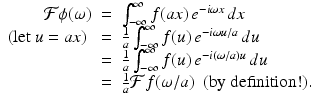
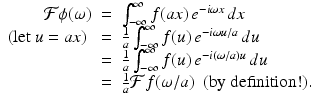
A similar argument applies when a < 0. (Why do we get a factor of 1∕ | a | in this case?)
Even and odd functions. A function f, defined on the real line, is even if 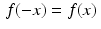 for every x. Similarly, a function g is odd if
for every x. Similarly, a function g is odd if 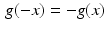 for every x. For example, the cosine function is even while the sine function is odd.
for every x. For example, the cosine function is even while the sine function is odd.
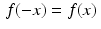 for every x. Similarly, a function g is odd if
for every x. Similarly, a function g is odd if 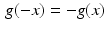 for every x. For example, the cosine function is even while the sine function is odd.
for every x. For example, the cosine function is even while the sine function is odd.Using Euler’s formula (4.4), 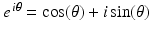 , we may write the Fourier transform of a suitable real-valued function f as
, we may write the Fourier transform of a suitable real-valued function f as
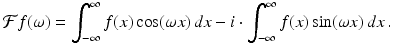
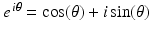 , we may write the Fourier transform of a suitable real-valued function f as
, we may write the Fourier transform of a suitable real-valued function f as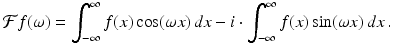
Now, if f is even, then, for fixed ω, the function 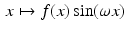 is odd, whence
is odd, whence 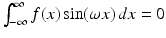 . Thus, an even function has a real-valued Fourier transform.
. Thus, an even function has a real-valued Fourier transform.
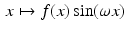 is odd, whence
is odd, whence 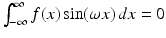 . Thus, an even function has a real-valued Fourier transform.
. Thus, an even function has a real-valued Fourier transform. Similarly, if f is odd, then 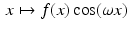 is also odd for each fixed ω. Thus,
is also odd for each fixed ω. Thus, 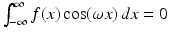 . It follows that an odd function has a purely imaginary Fourier transform.
. It follows that an odd function has a purely imaginary Fourier transform.
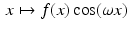 is also odd for each fixed ω. Thus,
is also odd for each fixed ω. Thus, 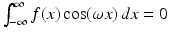 . It follows that an odd function has a purely imaginary Fourier transform.
. It follows that an odd function has a purely imaginary Fourier transform. Transform of the complex conjugate. For a complex-number-valued function f defined on the real line  , the complex conjugate of f is the function
, the complex conjugate of f is the function 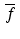 defined by
defined by
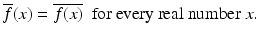
 , the complex conjugate of f is the function
, the complex conjugate of f is the function 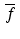 defined by
defined by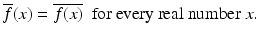
(5.9)
To uncover the relationship between the Fourier transform of 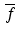 and that of f, let ω be an arbitrary real number. Then we have
and that of f, let ω be an arbitrary real number. Then we have
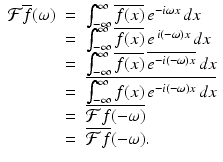 This proves the following proposition.
This proves the following proposition.
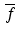 and that of f, let ω be an arbitrary real number. Then we have
and that of f, let ω be an arbitrary real number. Then we have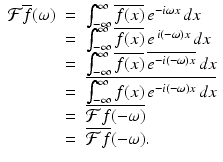
Proposition 5.4.
For an integrable function f defined on the real line, and for every real number ω,
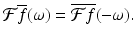
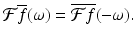
(5.10)
Example 5.5.
Let 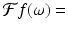 2 sin(ω)∕ω. Now let ϕ(x) = f(ax), where a > 0. That is,
2 sin(ω)∕ω. Now let ϕ(x) = f(ax), where a > 0. That is, 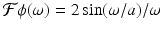 , which is the same as
, which is the same as 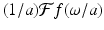 . This agrees with the scaling result (5.8).
. This agrees with the scaling result (5.8).
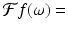 2 sin(ω)∕ω. Now let ϕ(x) = f(ax), where a > 0. That is,
2 sin(ω)∕ω. Now let ϕ(x) = f(ax), where a > 0. That is, 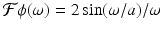 , which is the same as
, which is the same as 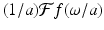 . This agrees with the scaling result (5.8).
. This agrees with the scaling result (5.8).Example 5.6.
Let 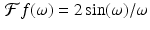 . Now let
. Now let
![$$\displaystyle{g(x) = f(x-2) = \left \{\begin{array}{cc} 1& \mbox{ if $1 \leq x \leq 3$,}\\ 0 &\mbox{ if $x <1$ or $x> 3$.} \end{array} \right.}$$
” src=”/wp-content/uploads/2016/10/A183987_2_En_5_Chapter_Equb.gif”></DIV></DIV></DIV>By the shifting/translation result (<SPAN class=InternalRef><A href=]() 5.6), we get
5.6), we get
Get Clinical Tree app for offline access
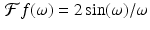 . Now let
. Now let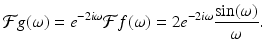
Example 5.7.
As an application of the shifting/modulation property (5.7), observe that
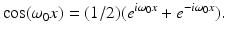 Thus, for any suitable f, take h(x) = f(x)cos(ω 0 x). That is,
Thus, for any suitable f, take h(x) = f(x)cos(ω 0 x). That is,
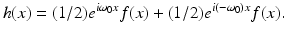 It follows that
It follows that
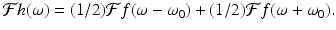
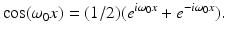
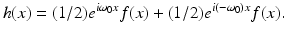
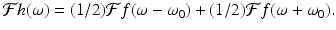
For a specific example, let 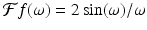 . With h(x) = f(x)cos(ω 0 x), we get
. With h(x) = f(x)cos(ω 0 x), we get
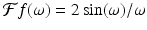 . With h(x) = f(x)cos(ω 0 x), we get
. With h(x) = f(x)cos(ω 0 x), we get