and Lori Ann Lewis1
(1)
Clinical Research Center of North Texas, Denton, TX, USA
Abstract
Precision is the attribute of a quantitative measurement technique like bone densitometry that refers to the ability to reproduce the same numerical result in the setting of no real biologic change when the test is repeatedly performed in an identical fashion. Like all quantitative tests in clinical medicine, no bone densitometry technique is perfectly reproducible. This is true even when the bone density test is performed in exact accordance with the manufacturer’s recommendations every time. If the test is not consistently performed in accordance with the manufacturer’s recommendations, the technique becomes less reproducible.
The Concept of Precision
Precision is the attribute of a quantitative measurement technique like bone densitometry that refers to the ability to reproduce the same numerical result in the setting of no real biologic change when the test is repeatedly performed in an identical fashion. Like all quantitative tests in clinical medicine, no bone densitometry technique is perfectly reproducible. This is true even when the bone density test is performed in exact accordance with the manufacturer’s recommendations every time. If the test is not consistently performed in accordance with the manufacturer’s recommendations, the technique becomes less reproducible.
The precision of bone density testing assumes great importance when the technique is used to follow changes in bone density over time. Because densitometry is not perfectly reproducible, the results on any given patient are not expected to be identical, even if the bone density in the patient has not actually changed. The only way to know that a real biologic change has occurred is to know if the precision error1 of the technique has been exceeded. This means that the precision must be quantified by performing a precision study. The precision, expressed as the root-mean-square standard deviation (RMS-SD) with the same units as the measurement or the root-mean-square % coefficient of variation (RMS-%CV), is then used to determine the minimum change in bone density that constitutes a real biologic change. This minimum change is called the least significant change (LSC). The LSC can then be used to determine the minimum interval between follow-up measurements.
Performing a Precision Study
The results of 3 PA lumbar spine DXA bone density measurements are shown in Table 7-1. These measurements on Mrs. B were all performed within a few minutes of each other, with only enough time between studies to allow Mrs. B to get off the scan table and be repositioned by the technologist. The same technologist positioned Mrs. B perfectly for all three studies and also analyzed all three studies according to the manufacturer’s recommendations. The mean or average value for these three studies was 1.021 g/cm2.
Table 7-1
Results From a Series of 3 PA Lumbar Spine DXA Studies on Patient, Mrs. B
PA spine DXA studies | |
|---|---|
Study #1 | 1.011 g/cm2 |
Study #2 | 1.030 g/cm2 |
Study #3 | 1.022 g/cm2 |
Mean | 1.021 g/cm2 |
SD | 0.010 g/cm2 |
CV | 0.010 |
%CV | 1.0 % |
Note that the numerical results of the three studies are not identical, even though each study was performed perfectly and no biologic change could have occurred in Mrs. B in the brief period that elapsed between tests. This reflects the imperfect precision of bone densitometry. In looking at Mrs. B’s measurements in Table 7-1, it is reasonable to ask by how much does each of the three measurements vary from the mean value? This can be found by subtracting each of the three measurements from the mean value, as shown in (7.1) through (7.3):
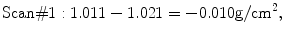
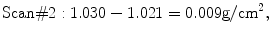
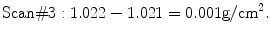
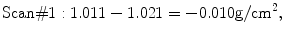
(7.1)
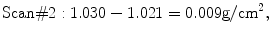
(7.2)
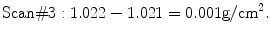
(7.3)
The question then becomes what is the representative variation from the mean for each of these measurements? An intuitive approach would be to find the average difference by adding the three differences found in (7.1) through (7.3) and dividing the sum by 3. This is neither mathematically correct nor possible, because the sum of the differences is 0, which cannot be divided. Instead, the formula in (7.4) is used. The three differences are squared to remove the minus signs. After squaring, they are added and the resulting total is divided by the number of measurements minus 1 (or in this case, 2). Then the square root is taken. The resulting value is the standard deviation (SD) for the set of three measurements on Mrs. B. The SD has the units of the measurement, g/cm2, and is the appropriate expression of the representative variability about the mean for the three measurements on Mrs. B. The SD is also the appropriate expression of the precision of the three measurements:
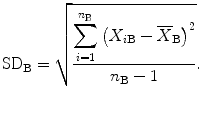
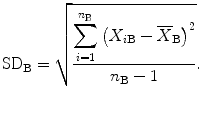
(7.4)
In (7.4), n B is the number of measurements on Mrs. B, and X iB is the actual value of the ith measurement and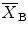 
(pronounced “ex bar”) is the mean BMD value for Mrs. B. The sum of the squared differences is divided by n−1 rather than n because, in this case, only two of the three measurements actually contribute independently to the calculation of the mean. In other words, if the average value and two of the three measured values that were used to calculate the average were known, the third measured value could always be determined mathematically. The third value is thus not independent. In the example presented, the SD for the set of three measurements on Mrs. B is 0.010 g/cm2 as shown in Table 7-1.
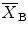(pronounced “ex bar”) is the mean BMD value for Mrs. B. The sum of the squared differences is divided by n−1 rather than n because, in this case, only two of the three measurements actually contribute independently to the calculation of the mean. In other words, if the average value and two of the three measured values that were used to calculate the average were known, the third measured value could always be determined mathematically. The third value is thus not independent. In the example presented, the SD for the set of three measurements on Mrs. B is 0.010 g/cm2 as shown in Table 7-1.Now that the SD and mean value for the three measurements on Mrs. B are known to be 0.010 g/cm2 and 1.021 g/cm2, respectively, it can be asked, “What proportion or percentage of the mean does the SD represent?” This is found by dividing the SD by the mean as shown in (7.5). This quantity is called the coefficient of variation (CV). When multiplied by 100 and expressed as a percentage, it is called the percent coefficient of variation (%CV) as shown in (7.6). The CV and %CV are alternative expressions of the precision of the measurement. For Mrs. B, the CV was 0.010 (after rounding) and the %CV, 1.0 %.
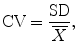
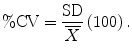
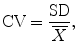
(7.5)
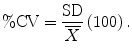
(7.6)
Although the SD, CV, or %CV for Mrs. B could be used in determining significant changes in PA lumbar spine bone density over time for Mrs. B, calculating individual precision values for every patient in a clinical practice that might be followed with bone densitometry is not practical. It is necessary to establish representative precision values for each skeletal site used for monitoring at a bone densitometry facility. This is done by performing a short-term precision study.
Short-Term Precision Studies
A separate precision study must be done for each skeletal site that might be used in following a patient. The precision for multiple regions within a skeletal site, such as the five regions of interest within the proximal femur, can be determined from a single proximal femur precision study.
The number of individuals and number of scans per individual needed for a precision study is determined by the degrees of freedom necessary to achieve the narrowest confidence limits for the precision estimate that are practical. Remember that one of the measurements on an individual will not contribute independently to the calculation of the mean for that individual. The number of measurements which do independently contribute is called the degrees of freedom (d.f.) for the study. For statistical validity, it is recommended that a short-term precision study has 30 d.f. [1]. Thirty d.f. are chosen to ensure that the upper limit for the 95 % confidence interval of the precision value is not more than 34 % greater than the calculated precision value. If only one person is studied, 31 tests must be performed to obtain 30 d.f. because one test will not contribute independently to the calculation of the mean. If 15 patients are studied, three tests per patient must be done because, again, only two of the three tests per patient will be independent (15 × 2 = 30). The specific combinations of the number of patients and number of scans per patient that are recommended for a short-term precision study are shown in Table 7-2. Although multiple scans on any one patient can be completed on the same day, it is preferable to spread the scans over a minimum of 1–2 weeks on any one patient.
Table 7-2
Combination of Number of Patients and Scans Per Patient for 30 Degrees of Freedom in a Precision Study
Number of patients | Number of scans per patient |
|---|---|
1 | 31 |
5 | 7 |
10 | 4 |
15 | 3 |
30 | 2 |
The following is the method for determining short-term precision as recommended by Glüer et al. [2]. Using the combination of 15 patients and three scans each for the sake of example, the average value, SD, and CV should be found for each of the 15 sets of three measurements, just as was done for the set of three measurements on Mrs. B. Rather than reporting the arithmetic mean of the 15 SDs or 15 CVs (adding the 15 values and dividing by 15) as the precision value, the root-mean-square SD (RMS-SD) or the root-mean-square CV (RMS-CV) is calculated as shown in (7.7) and (7.8). The RMS-SD and RMS-CV are preferred to the arithmetic mean SD and CV because the latter quantities tend to underestimate the Gaussian error2.
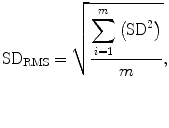
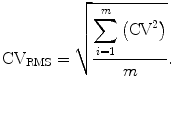
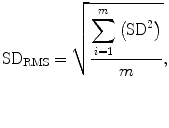
(7.7)
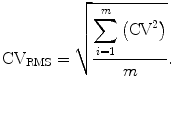
(7.8)
In (7.7) and (7.8), m is the number of patients. Using these equations, the 15 SDs or 15 CVs would be squared, summed, and then divided by the number of patients, 15. Then the square root is taken resulting in the RMS-SD or RMS-CV for the group of 15 patients. The RMS-CV can be expressed as a percentage, the RMS-%CV, by multiplying by 100.
In the following example, the short-term precision for the PA lumbar spine was calculated after 3 PA lumbar spine studies were performed on each of 15 patients within 4 weeks. The same technologist scanned all of the patients. Between each scan, the patient was repositioned. The individual values and the average value for each of the 15 patients are listed in Table 7-3. In all, 45 PA spine studies were performed (15 patients × 3 scans/patient = 45 scans).
Table 7-3
The Measured and Mean PA Lumbar Spine Values for 15 Patients in a Short-term Precision Study. All Values are in g/cm2
Patient | Scan #1 | Scan #2 | Scan #3 | Mean |
|---|---|---|---|---|
1 | 1.011 | 1.030 | 1.022 | 1.021 |
2 | 0.925 | 0.940 | 0.918 | 0.928 |
3 | 1.164 | 1.160 | 1.170 | 1.165 |
4 | 0.999 | 1.010 | 1.008 | 1.006 |
5 | 0.900 | 0.920 | 0.905 | 0.908 |
6 | 0.955 | 0.960 | 0.960 | 0.958 |
7 | 1.000 | 1.010 | 1.150 | 1.053 |
8 | 0.875 | 0.849 | 0.869 | 0.864 |
9 | 0.898 | 0.920 | 0.901 | 0.906 |
10 | 1.111 | 1.009 | 1.100 | 1.073 |
11 | 0.964 | 0.949 | 0.960 | 0.958 |
12 | 1.000 | 0.985 | 0.992 | 0.992 |
13 | 1.200 | 1.185 | 1.205 | 1.197 |
14 | 1.165 | 1.170 | 1.180 | 1.172 |
15 | 0.909 | 0.915 | 0.904 | 0.909 |
Mathematical Procedures Used to Calculate Precision
Step 1. The mean or average BMD, SD, CV, and %CV for the set of three scans for each of the 15 patients must be calculated. These results are shown in Table 7.4. Note that patient 1 in Table 7-3 and 7-4 is Mrs. B, for whom this calculation was made earlier.
Table 7-4
The Mean, Standard Deviation (SD), Coefficient of Variation (CV), and % Coefficient of Variation (%CV) for Each of 15 Patients in a Short-term Precision Study
Patient | Mean (g/cm2) | SD (g/cm2) | CV | %CV |
|---|---|---|---|---|
1 | 1.021 | 0.010 | 0.010 | 1.0 % |
2 | 0.928 | 0.011 | 0.012 | 1.2 % |
3 | 1.165 | 0.005 | 0.004 | 0.4 % |
4 | 1.006 | 0.006 | 0.006 | 0.6 % |
5 | 0.908 | 0.010 | 0.011 | 1.2 % |
6 | 0.958 | 0.003 | 0.003 | 0.3 % |
7 | 1.053 | 0.084 | 0.080 | 8.0 % |
8 | 0.864 |
