A. Atoms
–Matter is made up of atoms, which are composed of protons, neutrons, and electrons.
–Protons have a positive charge and are found in the nucleus of atoms.
–Neutrons are electrically neutral and are also found in the nucleus.
–Electrons have a negative charge and are found outside the nucleus.
–The atomic number (Z) is the number of protons in the nucleus of an atom and is unique for each element.
–The mass number (A) is the total number of protons and neutrons in the nucleus.
–Protons and neutrons are called nucleons because they are found in nuclei.
–In the notation AX, X is the unique letter(s) designating the element and A is the mass number.
–Electrically neutral atoms have equal numbers of electrons and protons (i.e., Z).
–12C is an atom of carbon that has 6 protons, 6 neutrons, and 6 electrons for an electrically neutral atom.
–Mass on the atomic scale is measured in atomic mass units (amu).
–One atomic mass unit is one-twelfth the mass of a carbon atom (12C).
–Protons and neutrons have a mass of ~1 amu.
–Electrons have a much smaller mass that is about 1,800 times less than protons and neutrons.
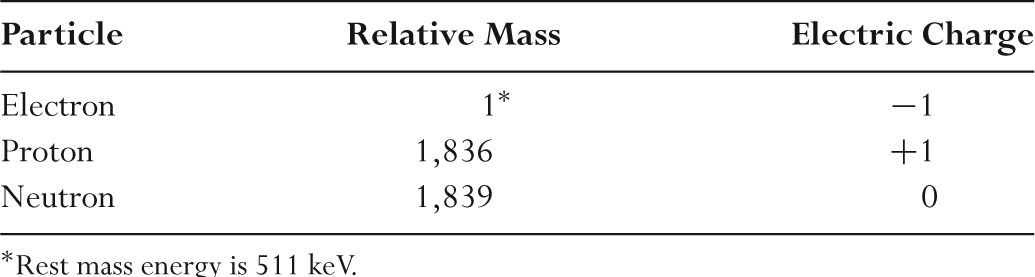
–Table 2.1 shows the relative mass and charge of atomic constituents.
B. Atomic structure
–The nucleus of an atom is made up of protons and neutrons and contains most of the atomic mass.
–In the Bohr model of an atom, electrons surround the nucleus in shells (e.g., K shell, L shell) as shown for tungsten in Figure 2.1.
–Each shell is assigned a principal quantum number (n) beginning with 1 for the K shell, 2 for the L shell, and so on.
–The number of electrons each shell can contain is 2n2.
–The K shell in tungsten (n = 1) has 2 electrons and the L shell (n = 2) has 8 electrons.
–The number of electrons in the outer shell (valence electrons) determines the atom’s chemical properties.
–The electron density of a substance is ρ N0(Z/A) electrons/cm3, where ρ is the density measured in grams per cubic centimeter (g/cm3) and N0 is Avogadro’s number.
–For most atoms making up tissues (e.g., oxygen, carbon, nitrogen, calcium), Z/A is equal to 0.5.
–For most patient tissues, electron density is proportional to the physical density ρ.
C. Electron binding energy
–Atomic electrons are held in place by the electrostatic pull of the positively charged nucleus.
–The energy required to completely remove an electron from an atom is called the electron binding energy.
TABLE 2.1 Characteristics of Atomic Constituents
–Binding energies are unique for each electron shell of each element.
–Atomic binding energy values are available in reference books.
–The binding energy of outer shell electrons is small.
–Outer shell electron binding energies are only a few electron volts.
–The binding energy of inner shell electrons is large.
–For most elements, the binding energy of inner shell electrons is measured in thousands of electron volts (i.e., keV).
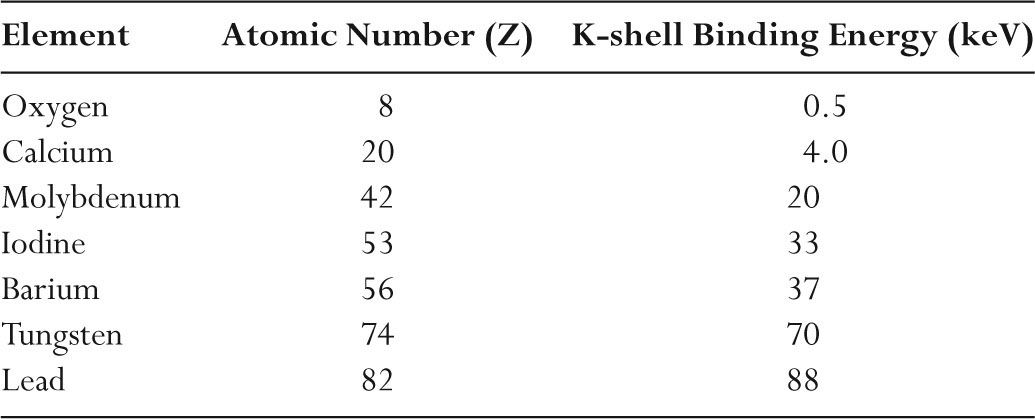
–K-shell binding energies increase with atomic number (Z) as listed in Table 2.2.
–Energetic particles can knock out inner shell electrons only if their energy is greater than the electron binding energy.
–A 50 keV electron cannot eject a tungsten K-shell electron (K-shell binding energy is 70 keV) whereas a 100 keV electron can.
–A vacancy in the K shell will be filled by an electron from a higher shell.
–Electrons moving from an outer shell to an inner shell may emit excess energy as electromagnetic radiation (i.e., characteristic x-ray).
–The excess energy may be transferred to an Auger electron, which then leaves the atom.
–Auger electron energy is the characteristic x-ray energy minus the binding energy of the outer shell electron.
–A K-shell vacancy results in either a characteristic x-ray or an Auger electron being emitted from the atom.
D. Ionization
–Ionization occurs when an electron is ejected from a neutral atom, leaving behind a positive ion.
–Electromagnetic radiation with sufficient energy to eject atomic electrons is called ionizing radiation.
–X-rays are a form of ionizing radiation.
–Gamma rays and ultraviolet radiation are also ionizing radiations.
–Ionizing radiation is categorized as either directly or indirectly ionizing.
–Radiation is directly ionizing when it is in the form of charged particles.
–Electrons and protons are both directly ionizing radiations.

FIGURE 2.1 Shell model of the Tungsten atom, which consists of 74 protons, 74 electrons, and 110 neutrons.
TABLE 2.2 Atomic Number and K-shell Binding Energy of Selected Elements
–The loss of energy by a charged particle increases with increasing charge and decreasing particle velocity.
–Energy lost from energetic particles can eject electrons from atoms or raise atomic electrons to more distant atomic shells (excitations).
–Uncharged particles are indirectly ionizing.
–Neutrons are indirectly ionizing radiations that interact with matter by first transferring energy to protons.
–Indirectly ionizing radiations include x-rays, and gamma rays.
–X-rays and gamma rays transfer energy to electrons.
–When an electron is removed from a (neutral) atom, it leaves behind a positive ion, and thus results in one electron-ion pair.
–The average amount of energy needed to generate one electron-ion pair in air is ~30 eV.
–A single 30 keV electron that is slowed down in matter thus produces~1,000 ionizations.
–30-keV electrons travel a distance of ~30 μm in soft tissue, comparable to the size of a very large cell.
–The energy transferred to electrons from x-rays is deposited locally.
A. X-ray absorption and scattering
–Three possible fates of x-rays incident on matter are penetration, absorption, and scattering.
–X-ray photons that pass through matter unaffected are said to penetrate an object.
–Very few x-rays (~1%) penetrate through an average-sized patient.
–When x-ray photons interact with matter, they transfer energy to electrons.
–Interactions of x-rays occur with the individual electrons in atoms.
–Interactions of x-ray photons with an oxygen atom are the same when the oxygen is bound to two hydrogen atoms as in a water molecule.
–X-rays may be absorbed and transfer their energy to electrons.
–X-rays may be scattered, resulting in a change of direction, and may lose energy to a scattered electron.
–These energetic electrons, in turn, lose energy by interacting with the electrons in adjacent atoms, thereby producing additional ionizations.
–An energetic electron may produce hundreds or thousands of additional ion pairs.
–Three ways that diagnostic energy x-rays interact with matter are (i) coherent scatter, (ii) photoelectric (PE) effect, and (iii) Compton scatter.
–Compton scatter and the photoelectric effect are important interactions in diagnostic radiology.
B. Coherent scatter
–Coherent scatter occurs when a low-energy x-ray photon is scattered from an atom without any energy loss.
–The wavelength of the scattered photon is the same as the wavelength of the incident photon.
–Coherent scatter is sometimes referred to as Rayleigh or classical scatter.
–Coherent scatter does not result in any energy deposition in the patient.
–Coherently scattered photons travel in a forward direction.
–Coherent scatter accounts for less than 5% of all photon interactions and is of minor concern in diagnostic radiology.
–Scattered photons will degrade image quality if they reach the image receptor.
C. Photoelectric effect
–The photoelectric (PE) effect occurs between tightly bound (inner shell) electrons and incident x-ray photons.
–In a PE interaction, the x-ray photon is totally absorbed (photoelectric absorption) by an inner shell electron and that electron is ejected from the atom.
–X-ray photons absorbed in PE interaction therefore “disappear”.
–As a result of the photoelectric interaction, a photoelectron is emitted and a positive atomic ion is left behind.
–The energy of the emitted photoelectron equals the difference between the incident photon energy and the electron binding energy.
–The photoelectron loses energy by ionizing other atoms in the tissue and contributes to patient dose.
–Outer shell electrons fill the inner shell electron vacancies, with the excess energy emitted as a characteristic x-ray or Auger electron.
–Auger electron energy is slightly lower than the characteristic x-ray energy.
–Figure 2.2A shows a photoelectric interaction.
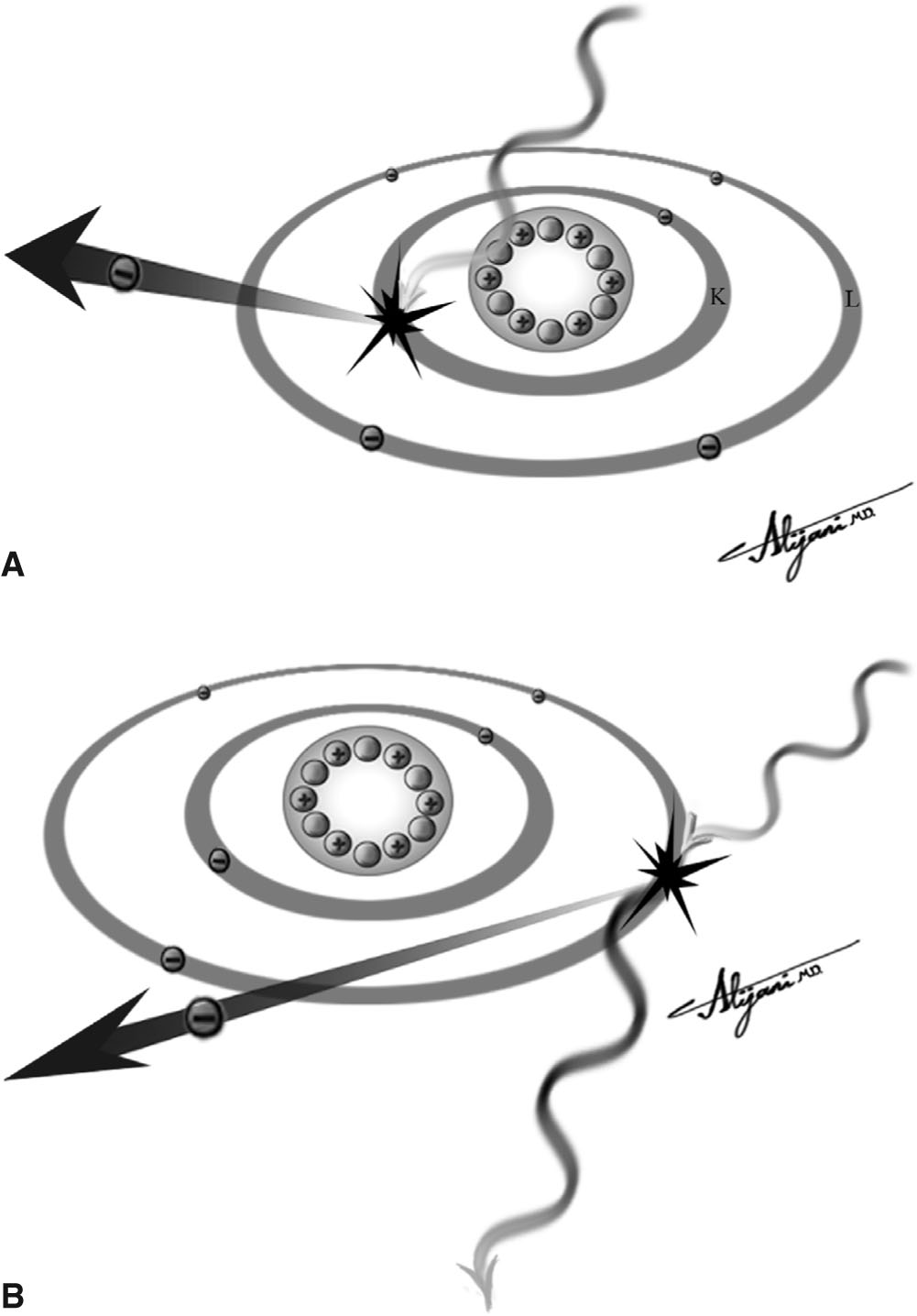
FIGURE 2.2 A: Photoelectric effect showing the total absorption of the incident x-ray photon and the ejection of a K-shell electron. B: Compton scatter showing the incident photon transferring kinetic energy to an outer shell electron and being scattered with a longer wavelength (i.e., lower photon energy).
D. Photoelectric effect probability
–For the PE effect to occur with a K-shell electron, the incident x-ray must have an energy greater than the binding energy of the K-shell electron.
–The absorption of photons increases markedly when the x-ray photon energy increases from below to above the binding energy of the K-shell electrons (K edge).
–The binding energy of the K-shell electrons (K edge) in iodine is 33 keV, and a sharp increase in the interaction of photons occurs at this energy.
–The probability of photoelectric absorption decreases rapidly as the photon energy (E) further increases above the K edge.
–Above the K-edge, photoelectric interactions are proportional to 1/E3.
–The more tightly bound an electron is, the greater is the probability of the PE effect if E is greater than the electron binding energy.
–The probability of photoelectric absorption increases with atomic number and is proportional to Z3.
–The PE effect is important when the atomic number (Z) is high and the photon energy is just above the K edge.
–Important K-shell binding energies are shown in Table 2.2.
E. Compton scatter
–In Compton scatter, incident photons interact with outer shell electrons.
–A Compton interaction results in a scattered photon that has less energy than the incident photon and generally travels in a different direction.
–A scattered (ejected or recoil) electron carries the energy lost by the incident photon as kinetic energy.
–This electron loses this kinetic energy by excitation and ionizing other atoms in the tissue, thereby contributing to the patient dose.
–Figure 2.2B shows a Compton interaction.
–As a result of the Compton interaction, a positive atomic ion, which has lost an outer shell electron, remains.
–Compton scattering can be modeled as occurring with free electrons, since the binding energy of outer shell electrons is so low.
–Compton interactions account for most scattered radiation encountered in diagnostic radiology.
–The scattered photon may undergo additional tissue interactions.
–Scattered photons may also reach the image receptor and degrade image quality.
F. Compton interaction probability
–The probability of a Compton interaction is proportional to the number of outer shell electrons available in the medium (i.e., electron density).
–Electron density of soft tissues is directly proportional to the physical density.
–The probability of Compton interactions is inversely proportional to the photon energy (1/E).
–Scattered photons may travel in any direction, including 180 degrees from the direction of the incident photon (backscattered).
–As the angle of deflection decreases, the energy retained by the scattered x-ray increases and the energy transferred to the recoil electron decreases.
–Energy transfer to the electron is a maximum when the photon is backscattered.
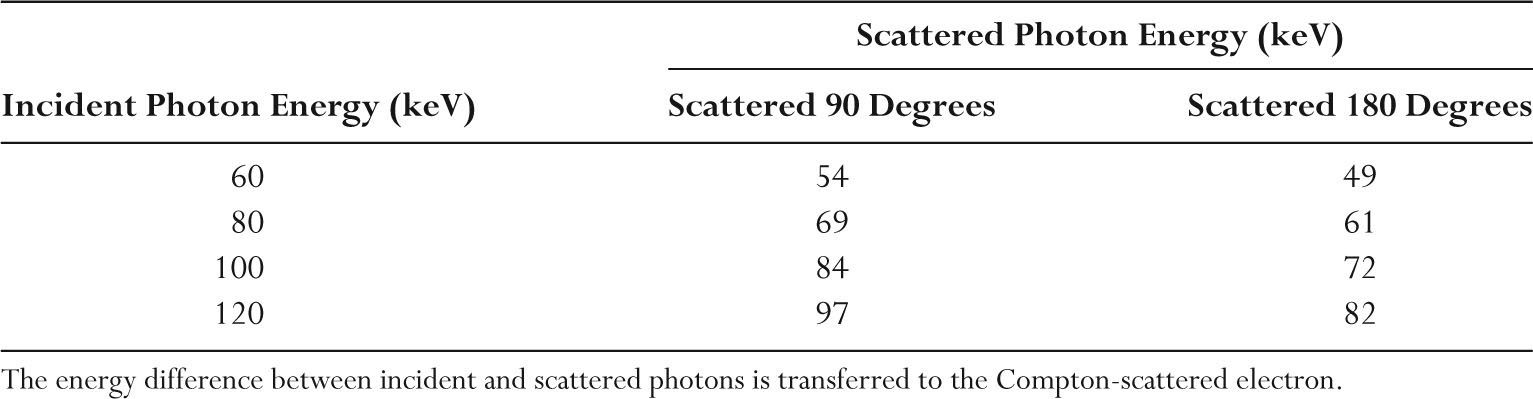
–The incident and Compton scattered x-ray energies at different scatter angles are listed in Table 2.3.
–A backscattered 60 keV photon will transfer 11 keV (18%) to the Compton electron.
–A backscattered 120 keV photon will transfer 38 keV (32%) to the Compton electron.
TABLE 2.3 Energies of Compton Scattered Photons
–For soft tissue, the PE and Compton effects are equal at 25 keV.
–In tissue, PE dominates at energies lower than 25 keV and Compton scatter dominates at energies greater than 25 keV.
–For bone, the PE and Compton effects are equal at 40 keV.
A. Linear attenuation coefficient
–The linear attenuation coefficient (μ) is the fraction of incident photons removed from the beam in traveling unit distance.
–Linear attenuation coefficients are expressed in inverse centimeters (cm−1).
–The attenuation coefficient accounts for all x-ray interactions, including coherent scatter, the PE effect, and Compton scatter.
–The linear attenuation coefficient increases with increasing physical density.
–Linear attenuation coefficients generally increase with increasing atomic number.
–In diagnostic radiology, attenuation decreases with increasing photon energy.
–An exception is at a K edge, where an increase in photon energy markedly increases attenuation.
–Monoenergetic x-rays are absorbed according to the exponential formula N = N0e –μt.
–N0 is the initial number of photons incident on an absorber of thickness t (cm), N is the number of photons transmitted, and μ (cm−1) is the attenuation coefficient.
–Monoenergetic is sometimes referred to as monochromatic.
B. Quantitative transmission
–When the value of μ is small, the numerical value of μ represents the fractional loss of photons.
–A μ of 0.01 cm−1 means that 1% of the incident photons are lost (i.e., absorbed or scattered) in 1 cm.
–A μ of 0.01 also means the remaining 99% of x-ray photons are transmitted.
–When the value of μ is not small, the fraction of transmitted photons can be determined from the expression e−μt.
–If μ is 0.5 cm–1, the fraction transmitted through 1 cm is e–0.5, or 0.61 (61%) and the fraction lost is 0.39 (39%).
–The value of soft tissue μ is 0.38 cm–1 at 30 keV, so the fraction of 30 keV photons transmitted through 1 cm of soft tissue is e–0.38 or 0.68 (68%).
–The value of soft tissue μ decreases to 0.21 cm–1 at 60 keV, with 81% transmitted through 1 cm.
–The value of bone μ is 1.6 cm–1
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree








