13.1 Introduction
Traditionally, physicists and engineers characterize an imaging system in terms of the resolution, noise, and contrast properties of the images produced by the system. Each of these properties (i.e., image quality characteristics) can be measured or modeled on most systems. In fact, system design, from an engineering perspective, relies heavily on optimizing these basic image properties. However, in a clinical context, what matters most is how these image quality characteristics affect the ability of physicians to interpret and characterize disease, with or without decision support systems. Therefore, this chapter aims to bridge the gap between basic image characteristics and image perception by reviewing some traditional image quality metrics and outlining how those metrics might be extended to measures of system performance that reflect the perceptual utility of an imaging system. The examples will be heavily based on X-ray radiography and computed tomography (CT) imaging but the concepts can be applied to most medical imaging modalities.
13.2 Theory of Image Quality
An image can be thought of as a two-dimensional (2D) (or nD) signal whose values (i.e., amplitudes) are related to the spatial distribution of some physical property being imaged (e.g., linear attenuation coefficients in CT). Most quantitative descriptions of image quality involve estimating summary statistics about this signal. Imaging systems can be quite complex and rely on sophisticated instrumentation to produce high-quality images, with each component’s performance limited by the underlying physical processes that form the basis of the image signal. Despite this real-world complexity, it is often possible to understand an imaging device’s overall performance by examining the cascade of constituent components that make up the entire system. Ultimately, however, what is of most interest are the final images and their physical and statistics characteristics. Therefore, here we focus mostly on analysis of the images produced and less on the underlying physical processes related to individual components of imaging systems. That being said, in a few instances, it will be useful to relate some basic image acquisition settings to their effect on image quality characteristics in order to better understand how such image quality characteristics impact image perception.
The mathematical modeling of image quality characteristics presented in this chapter relies heavily on signals and systems analysis (Blackman and Tukey, 1959; Dainty and Shaw, 1974; Dobbins, 2000) and specifically on linear systems theory along with Fourier analysis (Arfken and Weber, 1995). In such analyses, the image signal is decomposed into constituent spatial frequency components. This decomposition is illustrated in Figure 13.1, where a relatively complicated 1D signal is broken down into a small number of simple spatial frequencies. Note that here we do not aim to give a rigorous mathematical description of linear systems theory or Fourier analysis, but rather use those well-developed tools to describe helpful concepts and metrics that are commonly utilized to characterize the physical properties of images. Therefore, Fourier analysis will be used as a basis of several concepts, discussed below. The references above contain more detailed mathematical descriptions on those topics for interested readers.
Figure 13.1 A signal decomposed into its Fourier spatial frequency components. The signal can be represented by summing a series of sinusoidal signals of different spatial frequencies having amplitudes proportional to their contribution to the original signal. Note that, in the continuous domain, this summation is actually an integral over all spatial frequencies but this example is only showing a few discrete spatial frequency components.
For an image to be of any utility, it ultimately has to contain differences (i.e., contrast) between different materials or tissues of interest and the imaging system must be capable of representing features with sufficient detail (i.e., resolution) for the task at hand (e.g., detecting a microcalcification in mammography). Further, the degree of uncertainty (i.e., noise) in the measurements (i.e., pixels) that make up the image has a large impact on the perception and utilization of that image. Therefore, the physical image characteristics of resolution, contrast, and noise will be discussed individually below. Each characteristic will be defined and metrics associated with that characteristic will be given. Finally, the relationship between resolution, contrast, and noise and their joint effects on image perception will be discussed.
13.3 Spatial Resolution
13.3.1 What is Spatial Resolution?
The spatial resolution of an image defines the smallest structures in the image that can be spatially distinguished as separate. It sets a limit on the amount of detail that could be found in an image and largely determines the range of clinical tasks that could be performed with that image. There are many metrics that can be used to describe the resolution of an imaging system but one of the most common is the point spread function (PSF) and (or) its Fourier domain analogue, the modulation transfer function (MTF) (Bradford et al., 1999; Fujita et al., 1985; Giger and Doi, 1984; Workman and Brettle, 1997). The PSF is defined as the output signal given an input Dirac delta signal (i.e., an infinitesimally small signal whose integral is one). If the system is linear and shift-invariant, then the output of any input signal is given by the convolution of the input signal with the system’s PSF. Conceptually, the PSF describes the degree of blurring imposed on objects being imaged. Often the PSF has a Gaussian-like shape and a narrower PSF corresponds to an imaging system (or imaging condition) with better resolution. A typical metric to characterize a PSF is its full width at half maximum.
13.3.2 Resolution in the Fourier Domain
While the PSF describes the system resolution in the spatial domain, it is also possible to similarly describe resolution in the Fourier domain. The MTF is defined as the Fourier transform of the PSF (normalized to be one at a spatial frequency of zero). As mentioned above, in the spatial domain, the system output is given by the convolution of an input signal with the PSF. Because a convolution in the spatial domain corresponds to a multiplication in the Fourier domain, the system output in the Fourier domain is given by the Fourier transform of the input signal multiplied by the MTF. With this description, the system can be thought of as a band-pass filter which typically allows lower-spatial frequencies to pass while dampening higher spatial frequencies. In fact, the value of the MTF at a given spatial frequency represents the ratio of output to input amplitudes for signal components of that given frequency. In other words, at spatial frequency f, MTF(f) is the output amplitude of a sinusoid having frequency f, after having passed through the imaging system, relative to the input amplitude of that sinusoid. This conceptual description of the MTF is illustrated in Figure 13.2.
Figure 13.2 Illustration of how the modulation transfer function translates input frequencies into dampened output frequencies with reduced amplitude.
Because image details are encoded by high-spatial-frequency components, an MTF that allows high-frequency components to be preserved corresponds to an imaging system with strong resolving power. When comparing two systems or imaging conditions, a higher MTF implies better spatial resolution. Further, it is common to summarize the MTF curve into a single scalar statistic such as f10%, the spatial frequency at which the MTF reaches 10%. Higher f10% implies better spatial resolution. These statistics are illustrated in Figure 13.3.
Figure 13.3 Anatomy of a modulation transfer function (MTF) curve showing statistics, f50% and f10%, that are typically used as scalar metrics of resolution.
13.3.3 Measuring Resolution
Practically speaking, the manner in which MTF is measured is highly dependent on the imaging modality in question and the assumptions that can or cannot be made about the linearity and shift invariance of the system. Also, due to image acquisition, reconstruction, and geometric considerations, it is possible to have anisotropic resolution in which the MTF is not a single 1D curve, but rather a 2D (or nD) function of directionally dependent spatial frequencies. For example, in CT, the in-plane (axial) resolution is different than the z-direction resolution and the physical constraints that limit the resolution in each of those directions are fundamentally distinct. Thus, the MTF in CT is actually a 3D function.
Also, the simplifying assumptions of a linear shift-invariant imaging system are not strictly true on most real-world imaging systems. In radiography imaging, for example, different regions on the detector have different “views” of the X-ray source focal spot. This causes a PSF that is slightly different in different image regions, thus not meeting the definition of shift invariance. Despite these issues, it is often practical to apply these methods for comparison and characterization purposes under controlled testing conditions. In such cases, it is important to qualify measures of resolution with the conditions under which they were estimated, especially when comparing the performance of different systems or imaging conditions. The nomenclature of task transfer function (TTF) has in fact been utilized to indicate a limited condition (i.e., relevant to a specific imaging task) under which the MTF is measured.
13.3.4 Spatial Resolution and Pixel Size
Although it is not the intention of this chapter to describe how every imaging parameter in every modality affects resolution, it is useful to clarify a common misconception about the relationship between pixel size and resolution. Colloquially, the pixel size (physical dimension that pixel represents in millimeters) of an image is often quoted as synonymous with the image resolution. In reality, the pixel size does limit the maximum possible resolution in the image but is not the resolution in and of itself. Due to the physics of image acquisition (and reconstruction, where applicable), the actual resolution is usually less than the upper limit dictated by the pixel size.
For example, in modalities in which the final image is the result of computational reconstruction, such as CT, it is perfectly possible to reconstruct images with arbitrarily small pixels (e.g., micron-scale). However, due to physical processes that dictate resolution of clinical CT imaging systems, it is unlikely that micron-scale features could be resolved.
Another example is that of using interpolation to upsample and image to have smaller pixel size. The process does not improve the resolving power of an image (however, it may make the image appear less pixelated, which could have desirable psychophysical effects). Therefore, any quoted specification of an imaging system’s spatial resolution based on pixel size alone should be received with caution. It is much more meaningful and accurate to use an actual physical measurement of resolution, such as the MTF or TTF, as the basis of providing system specifications. Figure 13.4 provides examples of images with poor resolution/large pixels, poor resolution/small pixels, and high resolution/small pixels to illustrate this point.
Figure 13.4 Example of how pixel size alone does not guarantee good spatial resolution. Each image shows a circular disc rendered with high resolution and small pixel size (left), poor resolution and small pixel size (middle), and poor resolution and large pixel size (right).
13.3.5 Spatial Resolution and Image Perception
The spatial resolution of an imaging system ultimately limits the amount of information that an image can contain and also has a large impact on the visual impression of an image to a reader. Images with poor resolution can appear overly pixelated and/or blurry (similar to looking through an out-of-focus lens). The amount of details that a human or computational reader could perceive in an image is therefore directly associated with the underlying resolution of the image. Figure 13.5 gives an example of two CT images with different resolution and the MTF associated with each one.
Figure 13.5 Example of a low-resolution (left) and high-resolution (right) chest computed tomography (CT) image along with the modulation transfer functions (MTFs) corresponding to each image (bottom). Note how fine details and structures, such as small blood vessels in the lungs, are resolved in the high-resolution image but are blurred out in the low-resolution image. Also of note is the shape of the high-resolution MTF, which increases as spatial frequency increases (up to a point). In CT, this type of MTF shape is common and corresponds to reconstruction filters with so-called edge enhancement which attempt to selectively amplify the sharpness and contrast for edge-type features.
13.4 Contrast
13.4.1 What is Contrast?
All imaging modalities are based on the idea that different tissue types have differences in some given physical property. The ability to measure and visualize those differences is in fact what imaging provides, enabling the identification and diagnosis of a disease. Therefore, the goal of any imaging device is to interrogate a patient and produce an image highlighting differences between relevant tissues/structures. These differences are what we call contrast, defined as the difference in brightness (i.e., pixel value or signal) between features in the image. One could say in fact that an image without contrast is not an image. Contrast is usually conceptualized by imagining some feature of interest (e.g., a focal lesion) in the image “foreground” surrounded by a “background” region (e.g., liver parenchyma). The contrast of that feature is simply the difference in the feature’s average pixel value compared to the surrounding background’s average pixel value (sometimes the absolute value of that difference is used).
As contrast is the basis of an image, most engineering and implementation decisions are made in order to increase image contrast to better highlight differences between tissues of interest. The manner in which this is accomplished is highly modality-specific. As an example, in X-ray radiography imaging, scattered radiation has the effect of reducing image contrast and thus antiscatter grids are commonly used. In CT, the physical property being imaged is X-ray linear attenuation coefficients. As a general rule, there are larger differences in attenuation properties of tissues at lower X-ray energies and so reducing the kV of the X-ray tube (which shifts the X-ray energy spectrum to lower energies) has the effect of increasing image contrast. Further, it is very common to use contrast agents in the imaging process (e.g., iodine in X-ray imaging and gadolinium in magnetic resonance imaging (MRI)) to highlight vasculature, anatomical features, or tissue perfusion properties through enhanced contrast.
13.4.2 What is Contrast Resolution?
Contrast resolution refers to the minimum contrast that could be used to differentiate a feature from its surroundings. This quantity is commonly used synonymously with “low-contrast resolution” and “low-contrast detectability.” As will be discussed later in this chapter, contrast resolution is highly dependent on the noise and resolution properties of the image. However, in the absence of image noise, and assuming a digital imaging system with excellent spatial resolution, the image’s intrinsic contrast resolution is determined by the bit depth of the image (i.e., how many possible grayscale values can be represented in the image). For example, in a binary image with only two possible pixel values, 0 and 255 (i.e., black and white), the contrast resolution of this image is 255 because there is no way to visualize a contrast less than 255. On the other hand, an 8-bit image can have pixel values corresponding to all integers between 0 and 255. The contrast resolution of this image is 1. For this reason, quantization of pixel values (i.e., binning a spectrum of continuous floating-point number into discrete bins) has the effect of degrading contrast resolution.
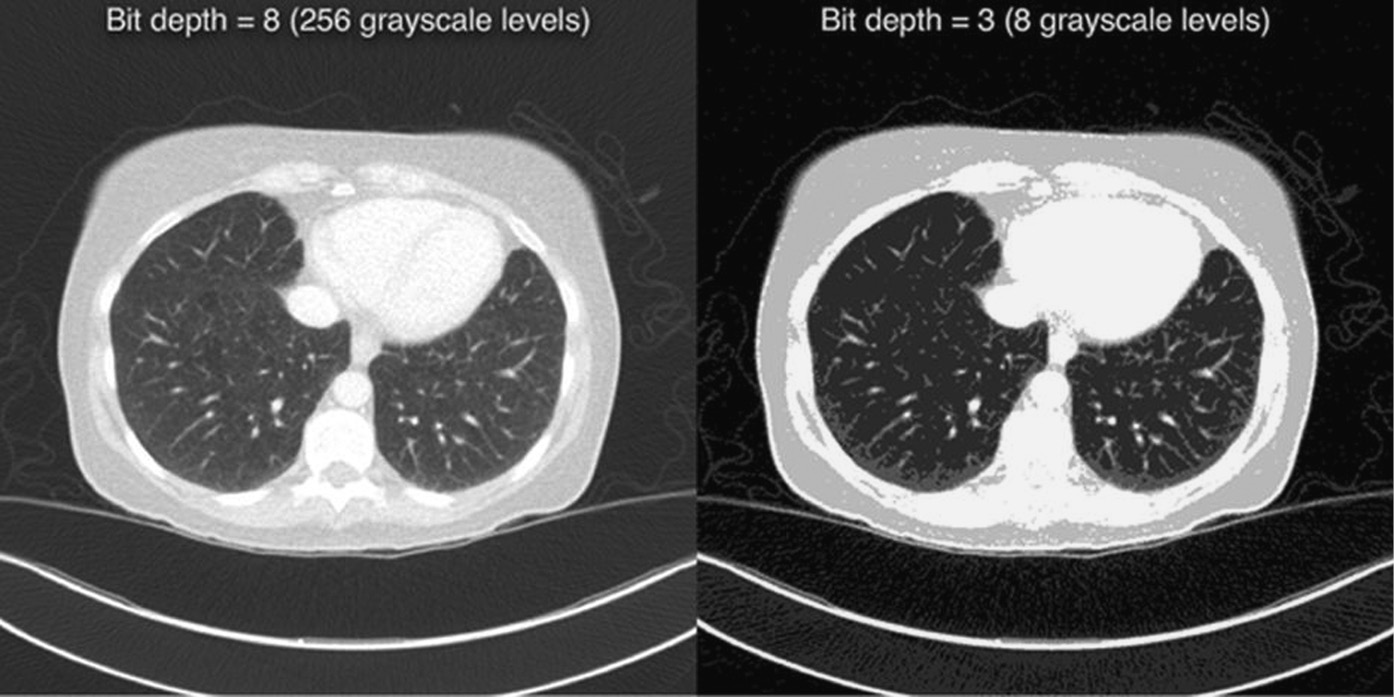
Quantization is a common method used to compress the size of image files. For example, a 16-bit 512 × 512 CT image uses 0.5 MB of disc space but an 8-bit image of the same dimensions uses only 0.25 MB. Unfortunately, such compression techniques are “lossy” (i.e., not all information in the original image is preserved) and aggressive quantization can cause so-called “banding” artifacts which perceptually make the image a somewhat artificial and cartoonish impression. Figure 13.6 shows an example of this artifact to illustrate the amount of information that is lost when an image has poor contrast resolution.
Figure 13.6 Example of two chest computed tomography images with different bit depth and therefore different contrast resolution. The left image contains 256 grayscale values and subtle details in the lungs can be differentiated while the right image has only eight possible grayscale values and suffers from banding artifacts and loss of details as a result.
13.4.3 Relationship Between Contrast and Spatial Resolution
Poor resolution can cause a reduction in image contrast. Conceptually, this is because poor resolution results in overly blurry features that blend into each other, thus reducing the differences in image intensity between those features. Mathematically, this can be explained in the spatial domain (PSF) or the spatial frequency domain (MTF or TTF). Imagine a small circular feature with a sharp distinct border (e.g., well-circumscribed pulmonary nodule). When that feature passes through the imaging system, its sharp edge profile is convolved with the imaging system’s PSF, resulting in a spatially diffuse edge. If the feature is small enough, this blurring of the feature’s edge on both sides results in an overall reduction in the maximum intensity within that feature (i.e., its contrast is reduced). Alternatively, in the spatial frequency domain, the MTF, by definition, describes how the amplitude of each spatial frequency component of the input signal is reduced by the imaging system. As a result, one interpretation of the MTF is that it describes how much contrast is reduced for different spatial frequencies. Figure 13.7 illustrates the relationship between contrast and spatial resolution.
Figure 13.7 Image with varying contrast and resolution. Each portion of the image was generated by starting with an idealized circular feature of a given contrast (increasing from left to right), and then blurring it with a given modulation transfer function (increasing from bottom to top). Notice how the image contrast decreases from top to bottom due to decreasing resolution.
13.5 Noise
13.5.1 What is Noise?
Medical images are based on a series of physical measurements (e.g., X-ray intensity) that contain some degree of uncertainty. The source of that uncertainty is highly dependent on the imaging modality of interest. For example, in X-ray-based imaging, the uncertainty is related to the random nature of generating and detecting X-rays, and/or the imperfect nature of transmitting subtle electronic signals through a series of complex electronic components. This uncertainty in raw measurements adds a degree of randomness to pixel intensity values in the final images. Noise is then defined as the random fluctuations of pixel values due to this statistical uncertainty. Mathematically, pixels in an image can be thought of as random variables, each having an associated probability distribution. Also, when considered jointly, the entire image itself can be thought of as a high-dimensional random process (i.e., a collection of random variables) with an associated joint probability distribution. It is useful to conceive of the image I(x, y) as being composed of a deterministic signal D(x, y) and a zero-mean random noise signal N(x, y), where I(x, y) = D(x, y) + N(x, y). Using this concept, noise can be quantitatively characterized using statistics of the random process.
13.5.2 How is Noise Characterized?
There are two noise characteristics that are most relevant to image perception, noise magnitude and noise texture. Noise magnitude refers to the degree of random fluctuations and is typically quantified by the standard deviation (or variance) of N(x, y). This can usually be easily measured in an image with a region of interest (ROI) within a uniform part of the image. In fact, image noise is often used synonymously with pixel standard deviation. A higher standard deviation means more random variability between nearby pixel values and thus higher noise magnitude.
Noise texture refers to the visual consistency of the noise (e.g., fine, coarse, blotchy) and can be quantitatively characterized by the noise correlations. The correlation between two random variables determines how those random variables tend to fluctuate with each other. For example, consider an ensemble of 100 noisy images (e.g., repeated scans of the same object under identical conditions). If two pixels, P1 and P2, have highly correlated noise, they will tend to fluctuate in concert with each other. Thus, if P1 is randomly low in one instance, P2 is also likely to be low in that same instance, and vice versa. If two pixels have uncorrelated noise, then P1 being low or high in one instance has no statistical bearing on the value of P2.
The noise correlations in an image can be characterized in the spatial domain by the noise autocorrelation function, which quantitativly describes the correlation between any two pixels as a function of the spatial separation between those pixels. In the spatial frequency domain, the noise correlations (and thus the noise texture) are characterized by the noise power spectrum (NPS), which is defined as the Fourier transform of the noise autocorrelation function (Giger et al., 1984, 1986). The integral of the NPS is equal to the pixel variance and thus, the NPS characterizes both noise magnitude and noise texture simultaneously, with the NPS amplitude determining the noise magnitude, and the NPS shape determining the texture. An NPS with a high proportion of low-frequency power corresponds to very grainy noise, while an NPS with high-frequency components corresponds to fine-grained noise. The relationship between noise magnitude, texture, and NPS is illustrated in Figure 13.8.
Figure 13.8 (a) Image with varying levels of noise magnitude and texture. The image is composed of a 4 × 4 grid of subimages and the noise power spectrum (NPS) associated with each image is shown in (b). Note that as the NPS shifts toward higher frequencies (from left to right), the noise becomes finer-grained. As the NPS amplitude increases (from bottom to top), the overall magnitude of the noise increases. Note that a given row of the image grid represents noise with equal pixel standard deviation but different noise texture. Therefore, visual examination of this image reveals that noise texture has a large impact on the perceived visual quality of the image. This implies that noise magnitude alone is insufficient to fully characterize the noise in an image. The rightmost column represents a special noise condition called white noise, which means the noise is uncorrelated. White noise has a flat NPS, as shown in the rightmost column of (b).
13.5.3 Noise and Image Perception
Both noise magnitude and texture have a strong impact on image perception. Often the overall perceived quality of an image is judged by its noise properties. It is useful to imagine how well a small image feature could be detected in images with varying noise magnitude and noise texture. It is obvious that increased noise magnitude decreases detectability and different noise texture would result in varying degrees of detectability depending on how similar the feature is compared to the noise texture grains. Such a scenario is illustrated in Figure 13.9 for synthesized images with CT-like noise. Another example for mammography-like noise is given in Figure 13.10.
Figure 13.9 Demonstration of how noise magnitude (top) and noise texture (bottom) affect detectability of a small image feature. Increasing noise magnitude results in decreased detectability and changing noise texture has a large impact on detectability. In this example, the noise texture goes from coarse (left) to fine (right). On the far-left image, the coarse texture grains have similar size and shape as the feature to be detected, making it very difficult to perceive the feature. In the spatial frequency domain, this means that the noise power spectrum strongly overlaps with the spatial frequency content of the feature.
Figure 13.10 Example of a mammogram-like image with no noise (left), white noise (center), and correlated noise (right). Each image contains small microcalcifications (arrows). Here it can be seen how correlated noise can mask important image features. NPS, noise power spectrum.
13.5.4 Relationship Between Noise and Resolution
It is sometimes convenient to discuss noise and resolution as separate concepts, and they do indeed describe different properties of an image. However, due to the physical processes associated with image acquisition in most imaging modalities, there tends to be a strong correlation between noise and resolution. It is almost always the case that changing the noise properties of an image will also change the resolution properties and vice versa. Generally speaking, increasing resolution has the effect of increasing noise, and decreasing noise has the effect of penalizing resolution.
CT imaging offers a classic example of this tradeoff. CT images are formed by acquiring a series of X-ray projection images at many different angles around the patient. Those projection images are run through an image reconstruction algorithm to form the familiar cross-sectional CT images. The image reconstruction settings have a large impact on the final noise and resolution properties of the CT images. The most common reconstruction method uses an algorithm called filtered back-projection, of which an integral part is a filtering step. The shape of the filter (also called a kernel) is a controllable setting and allows the user to trade off between noise and resolution properties to achieve images best suited for the diagnostic task at hand. So-called “sharp” kernels improve spatial resolution but suffer from increased noise while “soft” kernels have poor-spatial resolution but offer reduced noise. Also, the noise texture is strongly impacted by the kernel choice, with soft kernels corresponding to images with coarse (low-frequency) texture and sharp kernels corresponding to fine (high-frequency) texture. This tradeoff is illustrated in Figure 13.11.