4.1 Introduction
I will first describe early investigations of the effects of noise in images, starting with Albert Rose’s (1948) fluctuations theory approach to modeling of thresholds as a function of luminance (photon fluence). Sturm and Morgan (1949) used the Rose model to estimate the effects of X-ray image intensification in fluoroscopy and the contrast detail (CD) diagram phantom approach to measure human performance. The CD diagram shows the variation of the contrast required for signal detection at some defined reliability as a function of signal size. The work by Sturm and Morgan is discussed in detail in the next chapter, on the history of signal detection applications in medical imaging. The methods described by these authors became the standard evaluation approaches in medical imaging for the next 25 years. Next will be a brief introduction to signal detection theory (SDT) that was developed for radar applications in the early 1950s and was then applied to research in audition (hearing) in the late 1950s. Some suggestions were put forward in the early 1970s of how SDT might be applied in radiology.
This will be followed by experimental investigations in the early 1980s of human signal detection in uncorrelated (white) noise to determine whether our performance can be close to the limits predicted by SDT (the ideal observer concept) and whether humans could meet certain SDT constraints and requirements, such as the ability to do cross-correlation detection. At the same time, observer performance was being evaluated for a variety of tasks using simulated computed tomography (CT) images.
Once performance with white noise was reasonably well understood, investigations shifted in the early 1990s to tasks involving spatially correlated noise (also known as colored noise) and statistically defined (but simulated) correlated backgrounds to determine whether humans could compensate for the spatial correlations (prewhiten) as would be done by the ideal observer. During this period, observer SDT models became more elaborate – based on image domain vector-matrix calculations including channels. There are very good chapters of mathematical reference material on SDT and applications in a Society of Photo-optical Instrumentation Engineers (SPIE) handbook – see the introduction by Myers (2000) and details about models by Eckstein et al. (2000a). Background material on application of SDT to psychophysics can also be found in earlier classic books – see a collection of articles reprinted in Swets (1964) plus detailed explanations by Green and Swets (1966). One can access brief discussions of some other material online using “detection theory” in Wikipedia.
4.2 Albert Rose – The Beginning
Early theoretical analysis of signal detectability in noisy images was based on the Rose model, first described in 1948 for analysis of human vision. Albert Rose (1910–1990, Figure 4.1) was a physicist who joined the staff at Radio Corporation of America (RCA) in 1935 after gaining his PhD from Cornell University. His first assignment was to design a new television camera with greatly increased sensitivity. His work led, in 1939, to the image orthicon television camera tube that was several hundred times more sensitive than previous cameras. It was first used for military purposes during World War II before becoming the commercial television broadcast camera of choice until 1965. He was widely honored and wrote several books, including Vision – Human and Electronic (Rose, 1973).
Figure 4.1 Albert Rose.
In 1942 Rose became interested in the relative limitations in the light sensitivity of photographic film, television pickup tubes, and the human eye (Rose, 1946). In this paper he presented two important proposals: (1) the use of an absolute scale (quantum efficiency) for evaluating imaging system performance; and (2) a simple model for evaluating signal detectability by human observers – now known as the Rose model (Rose, 1948). Quantum efficiency is the fraction of incident photons that are actually used by the imaging system.
The Rose model allowed calculation of a signal-to-noise ratio (SNR) based on a particle fluctuation theory approach. This ratio describes the strength of the signal to be detected relative to a measure of the random fluctuations that interfere with signal detection. Details about SNR interpretation are discussed below.
A few years later Peterson et al. (1954) presented a rigorous (ideal observer) SDT based on Bayesian probabilistic analysis. The Rose model is useful for simple calculations but has a very narrow range of validity. The Rose model will be outlined in this section. Burgess (1999a) presented details of the model and its relationship to the ideal observer approach.
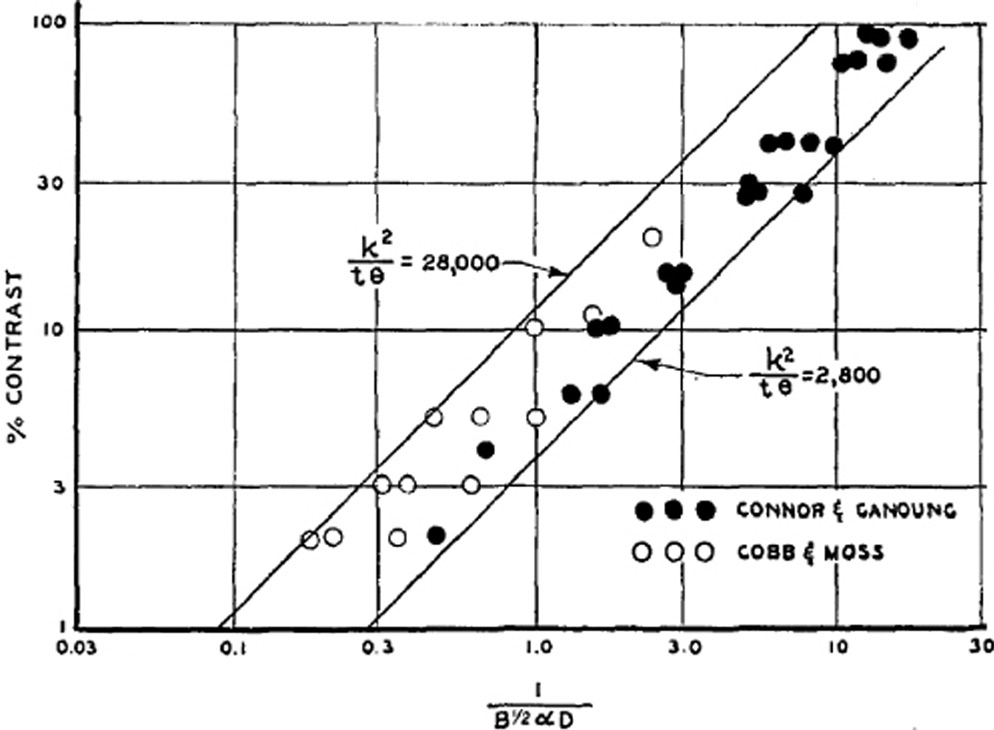
Rose (1948) used a particle-based fluctuations theory to evaluate human data from detection measurements at a variety of light levels. The data came from measurements published in 1928 by Cobb and Moss for luminances between 10−4 and10−1 footlamberts (Ft-L, where 1 Ft-L = 3.43 candelas/m2)plus measurements published in 1935 by Connor and Ganoung for luminances between 1 and 100 Ft-L. Note that the upper limit for scotopic (completely dark-adapted) vision is about 3 × 10−3 Ft-L and the transition mesopic region is from about 3 × 10−3 to about 0.3 Ft-L, where both rods and cones contribute. The photopic region is above the mesopic region and cone vision dominates. Rose assumed that observer vision was limited by photon fluctuation and used the following contrast threshold equation to compare to the data:
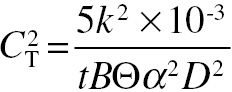 (4.1)
(4.1)The parameters are k, the threshold SNR which he had found to be about 5 based on observer experiments, the visual integration time t (in seconds), the scene brightness B (in Ft-L), the quantum efficiency of the eye Θ (with a maximum value of unity), the angle subtended by the test object α (in minutes of arc), and the eye lens aperture D (in inches). Rose produced a reduced plot to combine all data. He plotted contrast threshold as a function of the product, αD√B, and the results (Figure 8 from his paper) are shown in Figure 4.2. The lines bound the data with the product k2/tΘ between 2.8 × 103 and 2.8 × 104.
Figure 4.2 Contrast thresholds for signal detection in noiseless backgrounds under a range of luminances, B, from 10−4 to 100 Ft-L. The dark symbols are for scotopic vision and the open symbols are for photopic vision. The highest quantum efficiency is toward the lower right corner. The parameters are explained in the text. The diagonal lines indicate theoretical predictions for an ideal observer with the parameter products indicated.
One can make an estimate of the quantum efficiency using reasonable estimates of 5 for the threshold SNR and 0.2 seconds for the integration time of the eye. This gives estimates of Θ approximately 0.5% for photopic vision and 5% for scotopic vision. These values are in not bad agreement with later results obtained by more sophisticated methods. They are obviously dependent on the selection of the values for k and t.
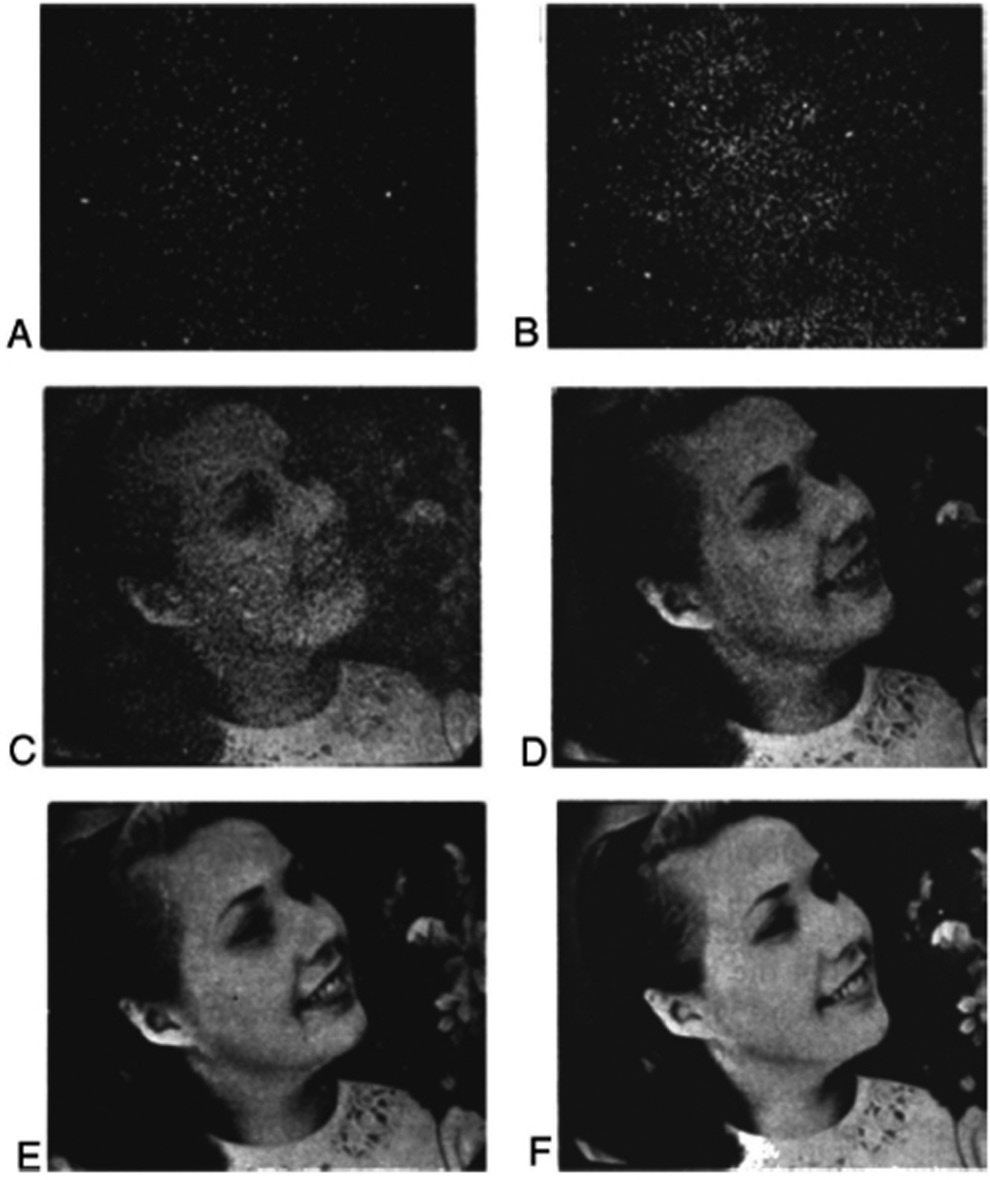
Later Rose (1953) used the images shown in Figure 4.3 to demonstrate the maximum amount of information that can be conveyed by various known numbers of photons. Bob Wagner, Bob Jennings, and I had the pleasure of having dinner with Albert Rose in 1984, when he mentioned that he had had great difficulty in convincing the journal reviewers that the photographs in the figure were legitimate.
Figure 4.3 Picture used by Rose (1953) of woman with flowers, to demonstrate the maximum amount of information that can be represented with varying numbers of photons. The photon counts change by roughly a factor of 7 between images. Each photon is represented as a discrete visible speck. The inherent statistical fluctuations in photon density limit one’s ability to detect or identify features in the original scene.
4.3 What is Signal-to-Noise Ratio?
Noise is a ubiquitous problem in science and engineering. Anyone attempting to define an SNR must somehow characterize the strengths of both signal and noise. In this chapter I will assume that the term “noise” refers to truly random noise – as a result of a random process. The term “noise” is also used in contexts. This issue is discussed in my chapter on signal detection in medical imaging (Chapter 5), which includes patient structure backgrounds. The theory of signal detectability provides a definition of SNR that is not arbitrary (see Chapter 18). SNR calculations can be very misleading if not done correctly. The key point is that attempts to minimize the effect of noise on task performance, by filtering, for example, must take into account the nature of the task. This leads to very different optimization strategies for different tasks.
The Rose model approach, as we have used it in medical imaging, is valid for evaluation of detectability of sharp-edged signals at known locations in white noise added to a known mean background. This is referred to as the signal-known-exactly/background-known-exactly (SKE/BKE) task. The development of the Rose model is as follows. Let the mean signal (with area A) be described by an increment of E[∆ Ns] equal to E[A∆ ns], photons above the background mean, where E[…]denotes expectation value. The background has a mean of E[NB] expected photons within the signal boundary and E[nB] expected photons per unit area. The background photon fluctuations have a standard deviation per unit area of σNB. Let the signal contrast, C, be defined as C = E[∆ ns]/E[nB]. Rose defined SNR as
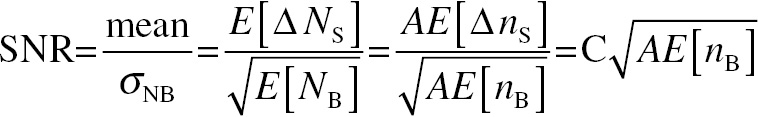 (4.2)
(4.2)A number of assumptions are needed for the Rose model to be equivalent to modern SDT based on SKE/BKE cross-correlation detection in Gaussian noise:
1. The Rose model neglects the fact that noise in the potential signal location has unequal variances for the signal-present and signal-absent cases. Hence the Rose model is an approximation that is valid only in the limit of low-contrast signals.
2. The photon noise has a Poisson distribution, whereas the above SDT approach was based on a Gaussian distribution. We need to assume that photon densities are large enough that Poisson noise can be approximated by Gaussian noise with the same mean and variance.
3. Rose used completely defined signals at known locations on a uniform background for his experiments and analysis, so the SKE and BKE constraints of the simple SDT analysis were satisfied.
4. He assumed perfect use of prior information about the signal.
5. He used a flat-topped signal at the detector plane (which is only possible when there is no imaging system blur). This assumption meant that integration of photon counts over the known signal area is equivalent to cross-correlation detection.
Rose used his model to assess the detectability of signals, in that he asked the question, “What SNR was required in order to detect a signal?” His approach was to use a constant, k, defined as the threshold SNR, and to suggest that the value of k must be determined experimentally. The signal was expected to be reliably detectable if its SNR were above this threshold. Once k is selected, the corresponding contrast threshold CT is given by
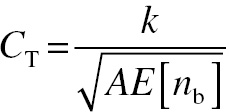 (4.3)
(4.3)Using this definition of threshold, SNR has the unfortunate effect of mixing the measure of relative signal strength (SNR) with the proposed decision accuracy and the observer’s decision criterion. However, it followed the convention of the day. People unfamiliar with SDT sometimes still use the threshold SNR concept. Some early publications had used a value of k equal to unity. Rose performed experiments and concluded that k was somewhere between 3 and 7, with a number around 5 being the most likely value. Subsequently, people in radiology using the Rose model discussed values in the range of 3–5. Given the confusion about the definition of a “threshold” and the subjective nature of the experiments (more on this below), it is not worth pursuing this topic further except to make one point. In 1980, I did experiments in collaboration with several other people and found human observer efficiencies near 50% for a variety of tasks (Burgess et al., 1981). Free-response experiments described by Burgess (1999a) gave results consistent with a value of 5 for k when an arbitrary number of known discs were located anywhere within a defined region of about 1000 times the signal area. This immediately suggested that one could have used Rose’s estimate of k of about 5 to predict about 50% human signal detection efficiency in white noise in the late 1950s when observer efficiency was first defined (Tanner and Birdsall, 1958).
4.4 Introduction to Signal Detection Theory
4.4.1 The Likelihood Ratio Approach
I will first give a brief summary of the main principles of SDT and then describe some history. A more complete description of the mathematics is given by Myers (2000) and by Abbey and Eckstein (2000) in the same book. The analytical approach depends on the decision task (the intended use of the image) – which is usually either classification or estimation based on data. A simple binary classification task will be discussed here since it is the easiest to understand.
Assume that we are given a noisy digital image described by the column vector, g. In a binary decision task it is known that one of two situations (events, j, with j = 0 or 1) is true. For example, it may be that the alternative events are: a signal is present or absent, or alternatively one of two signals (A or B) is present.
The observer will consider two hypotheses, hj, about which event actually occurred given the conditional a priori probability density of the image data, p(g | hj), and the a priori probability density, p(hj), for each hypothesis being correct. The observer’s problem is to decide which hypothesis is most likely to be correct. SDT gives a method of determining the best solution to this decision problem, which is used by the ideal observer. The analysis is based on Bayes’ theorem. It can be shown that the a posteriori probability density, p(hj | g), of a particular hypothesis, hj, being true is described by
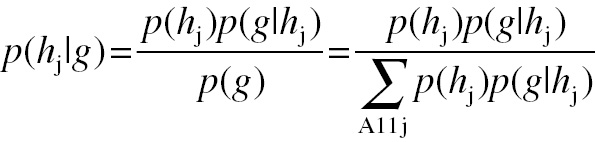 (4.4)
(4.4)Frequently one wants to evaluate the evidence provided by the event independently of the a priori probability of the hypotheses or it may be that the two events have equal a priori probability. Then the evidence for the correctness of the hypotheses can be summarized by the likelihood ratio, defined as
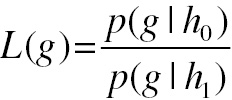 (4.5)
(4.5)Any monotonic function of the likelihood ratio can also be used to evaluate the evidence, since such transforms will not change decisions. It is often convenient to use the log(likelihood ratio), denoted by λ(g), as a decision variable. Since noise is present, the decision variable will be a random variable. The value of the decision variable is then compared to a criterion value to arrive at a choice of hypothesis. The criterion value will affect the false alarm and signal miss rates. So the decision maker will select a criterion that gives desired rates for the two types of errors, usually based on a priori probability of the presence of a signal and the costs associated with the two kinds of errors.
The calculation of the likelihood ratio is only straightforward for a limited range of tasks. The simplest task concerns a decision about the presence or absence of a signal under SKE/BKE conditions. The calculation is particularly tractable if the noise is additive and uncorrelated with a Gaussian probability distribution. For this situation, analysis based on the log(likelihood ratio) indicates that the optimal strategy is to use the signal itself as a template to cross-correlate with the data to obtain a decision variable. This procedure is also known as matched filtering.
The likelihood ratio approach was first described by V.A. Kotelnikov (1908–2005), a Russian communications engineer and information theory pioneer. He is best known for having discovered, independently of others, the Nyquist–Shannon sampling theorem. Kotelnikov began investigating signal detection in noise in 1946 but was unsuccessful in getting his work published in the Russian literature (apparently the editors claimed lack of interest to communications engineers). Finally his dissertation was published in 1956 (in Russian), and subsequently translated from the Russian by R.A. Silverman and published in English (Kotelnikov, 1959).
4.4.2 The Matched Filter
The prewhitening (PW) matched-filter model for SKE signal detection comes up very frequently in the medical imaging literature. It was first developed by D.O. North (1943, 1963) of RCA Laboratories to analyze optimization of radar system detection performance during World War II. Van Vleck and Middleton at the Harvard Radio Research Laboratory nearly simultaneously discovered it. North’s main activity was developing electronic tubes. I was told in the 1980s by someone at RCA that he was informed about the detection optimization problem, solved it in one afternoon, and never regarded it as a particularly significant achievement. His paper is a model of clarity of thought and a pleasure to read. North’s work was first described in an RCA internal document, which was subsequently distributed to generations of graduate students in mimeographed form. The copies eventually became almost unreadable, so the report was finally published in a refereed journal in 1963 so a clean copy would be available for reference. Related radar reception work was done at the Massachusetts Institute of Technology Radiation Laboratory during World War II.
North asked the question, what is the best filter to use at the radar receiver so that its output gives the best contrast between signal and noise? In other words, if the signal is present, then the filter should give a sharply peaked output, whereas, if the signal is not present, the filter should give as low an output as possible. It was assumed that the filter designer knew the temporal profile and arrival time, t0, of the signal (a short radar echo pulse of a particular shape). So the problem is to detect a known signal, s(t), in a waveform, x(t), with additive random noise, n(t), by use of a filter with an impulse response, h(t). The filter input and output functions are
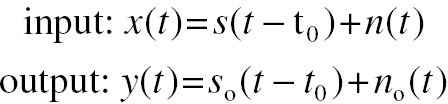 (4.6)
(4.6)where
and∗denotes convolution.
North chose to select the optimum filter by maximizing the ratio of the signal amplitude to the noise amplitude of the output at some instant in time, based on the known arrival time of the signal. Since the noise is a random variable, it was characterized by the mean-square value of its amplitude, E[n2o(t)]. This gave the following quadratic ratio, ρ(tm), to characterize the relative strength of output signal and noise at tm:
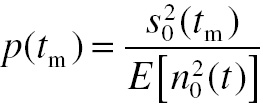 (4.7)
(4.7)Note that use of this equation does not consider or guarantee that the output signal will in any way resemble the input signal. The only concern is to maximize a scalar quantity at tm. The analysis is easiest to do in the frequency domain, so let capitalized terms represent the Fourier transforms of the lower-case terms:
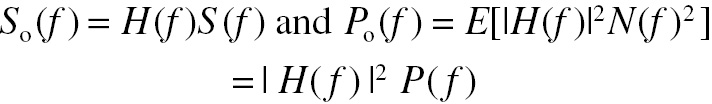 (4.8)
(4.8)P(f) and Po(f) are the power spectra of the input and output noise. The power spectra can have arbitrary form; there is no need for the noise to be uncorrelated (white). The goal is to determine the particular filter that maximizes the ratio ρ(tm). It can be shown that
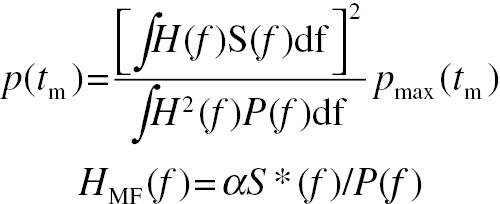 (4.9)
(4.9)The parameter α is an arbitrary scaling factor that can be taken into consideration when selecting a decision criterion. The function S*(f) is the complex conjugate of S(f). Furthermore, the optimum measurement time equals the known arrival time. This is a description of the PW matched filter, by direct (one-step) filtering of the input. Prewhitened matched filtering can also be understood by consideration of the following two-step procedure. The first step involves a filter, H(f), that converts the input fluctuations to white noise. This filter is described by H1(f) = 1/√P(f). When the filter is applied to the input, the result is x2(t) = h1(t)∗s(t − t0) + w(t), where w(t) is white noise. This is the so-called “prewhitening” procedure. The signal, s2(t), in x2(t) has a different profile than the one in x(t) because of the filtering. The optimum strategy is now to filter x2(t) using a second filter, h2(t), optimized to detect the revised signal profile. It can be shown that the optimum second filter and two-step filtering results are
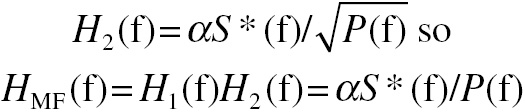 (4.10)
(4.10)So the one-step and two-step total matched filters are the same. The two-step description makes the notion of “prewhitening” directly observable. It is hidden in the one-step procedure. The term “observer template” is frequently encountered in the medical imaging signal detection literature. What it means is this. Rather than doing frequency domain matched filtering, the observer can use a template, h(t) in the notation of this section, to cross-correlate with image data. The optimum template is the inverse Fourier transform of the PW matched filter.
One other point is worth noting. In receiver operating characteristic (ROC) or “yes/no” decision tasks where a signal may or may not be present, the signal peak amplitude (or profile scaling factor) and the template (or filter) scaling factor α must be known to the decision maker in order to select an appropriate decision criterion. This is not the case in M-alternative forced-choice (MAFC) experiments where only one (known) signal is present together with M – 1 known and equally detectable alternatives. The optimum decision strategy is to select the alternative with the highest likelihood ratio value. The template scaling parameter does not come into play and can be any nonzero value. It does not need to be known to the decision maker since it is applied to all M alternatives.
4.4.3 The Ideal Observer
More complete ideal observer analysis based on the likelihood ratio approach was developed by Peterson et al. (1954), also to evaluate optimization of radar systems. It was subsequently adapted for analysis of human auditory and visual signal detection and discrimination analysis. This approach is also described in some detail by Burgess (1999a). For simple situations the matched-filter approach and the likelihood ratio approach give identical results. For more complex situations, the likelihood ratio approach brings the full power of probability theory analysis to the problem and is much superior. Woodward and Davies (1952) did a related development of SDT using Jeffrey’s theory of inverse probability.
Tanner and Swets (1954) did visual signal detection experiments, which gave results that were inconsistent with the previously common view that visual thresholds represented some “hard” lower detectability limit. This latter theory is known as “high-threshold” theory – the view was that detection probability remained at zero until some particular signal amplitude was reached. Tanner and Swets found that visual signal detection probability increased monotonically from zero as signal amplitude was increased from zero. Tanner and Swets (1954) also showed the equality of visual signal detectability values, d′, determined by “yes/no” ROC and multiple location forced-choice methods. These results were regarded as an important validation of the application of SDT to human subjects and a demonstration that results of different psychophysical tests can have meaning in spite of different procedures.
4.4.4 Observer Efficiency
The next classic paper in SDT was the introduction of the concept of observer efficiency by Tanner and Birdsall (1958). Let EI be the signal energy required for the ideal observer to detect a signal at a given performance accuracy (90% correct in a two-alternative forced-choice (2AFC) task, for example). Let ET be the signal energy required for the observer under test to detect the same signal at the same accuracy under the same conditions. They calculated efficiency at the selected decision accuracy (or performance level, P) using a ratio of these two energies. It should be carefully noted that their definition could be applied to tasks where the signal is only known in the statistical sense (SKS) as well as for SKE conditions.
Barlow (1962) calculated efficiency in a different manner, using d′ values for the two observers at a selected signal amplitude, A. It should be carefully noted that the two definitions are only equivalent in the case where the values of d′ are proportional to signal amplitude. This situation is rarely true for human observers and is not true for the ideal observer if the signal is not known exactly but is only defined statistically. The two definitions of efficiency are
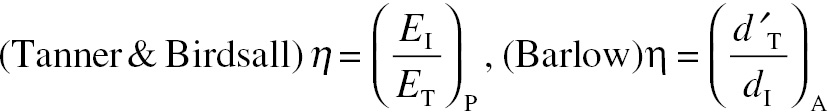 (4.11)
(4.11)In the context of radiological or nuclear medicine imaging, Tanner and Birdsall’s definition can be thought of as comparing how many photons the two observers need to perform the same task with the same accuracy. For magnetic resonance imaging it would be the ratio of image acquisition times, all else being equal. The efficiency approach was used for evaluation of a few auditory signal detection and discrimination experiments in the late 1950s. This was possible because auditory signals and noise were easily generated and recorded. Efficiencies were found to be very low (1% or less) so the ideal observer model was never considered as a starting point for modeling of hearing. The low auditory efficiency is not surprising because the observer must make precise use of a known waveform and arrival time to do cross-correlation. We are not able to do this. There were no investigations of visual efficiency because the required display hardware was not available.
The efficiency approach was first applied to vision by Barlow (1978) using computer-generated random dot images. He was attempting to measure cortical spatial tuning curves that would be analogous to the contrast sensitivity curves for luminance (grayscale) patterns. The basic idea was that the small dots were reliably transduced by the retina and that any spatial tuning that was found might be due to receptive fields in the visual cortex. Barlow used Poisson statistics to generate patterns and chose observer efficiency as the measure of pattern detectability. He consistently found efficiencies of approximately 50%, independent of pattern size or shape.
Subsequently, Burgess and Barlow (1983) used random dot patterns with Gaussian statistics to allow independent adjustment of the mean and the variance. This, in turn, separated effects due to sampling efficiency (which is an estimate of the accuracy with which the appropriate signal detection template is used and positioned) from effects due to intrinsic observer variability (internal noise). Their measurements suggested that virtually all of the reduction in human dot detection efficiency was due to centrally located internal noise. Sampling efficiency appeared to be approximately 100% for a wide range of random dot patterns. The word sampling was selected to be consistent with the original formulation of decision accuracy by Fisher. The work by Burgess and Barlow was actually done in 1979 and then submitted for publication. Unfortunately the journal moved its editorial office and all records of the manuscript submission and referee’s comments were lost. This oversight was subsequently corrected and the paper appeared in print several years later.
4.5 One-Dimensional White-Noise Experiments
Pollehn and Roehrig (1970) were the first to measure the contrast sensitivity function (CSF) in the presence of visual noise. They generated one-dimensional (1D) sinusoidal signals with added 1D white noise in each raster line for display on a linearized television monitor. The noise will be white in 2D because noise in adjacent raster lines is uncorrelated. They made a number of measurements using two methods. One was the method of limits where the signal amplitude was decreased from a large value until the observer (subjectively) reported that it could no longer be “seen.” The amplitude was lowered further and then increased until the observer reported that it could be “seen” again. The descending and ascending thresholds were then averaged.
They used a second method for three selected frequencies. The observer was shown a randomly selected test pattern of one of these frequencies with amplitudes near the previously estimated thresholds and asked which pattern was present. Thresholds were defined as the amplitude that gave 50% correct responses. There was good agreement between the results for the two methods.
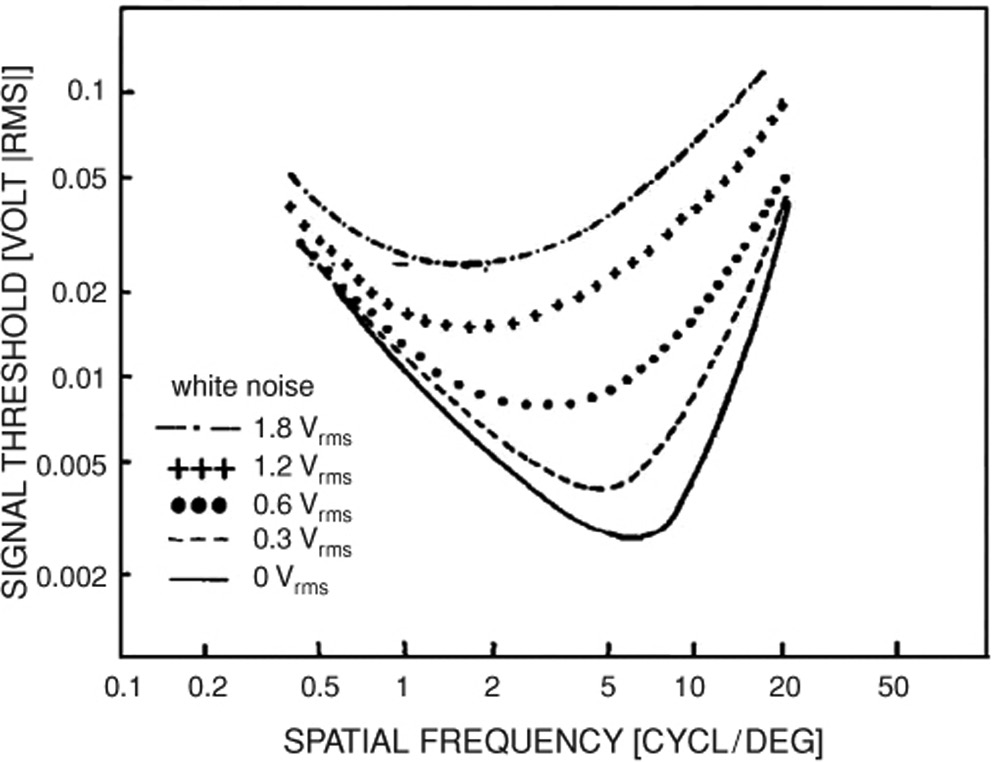
They did a variety of experiments with six observers. CSF values for five noise levels are shown in Figure 4.4. They did CSF measurements 4 months apart to evaluate reproducibility. They also checked for consistency by using several viewing distances and varied the number of cycles in the sinusoidal signals. When the image noise level was varied, they found that the signal threshold values STH as a function of the root mean square value of the image noise, N, could be described using
Figure 4.4 Measured amplitude thresholds from Figure 7 of Pollehn and Roehrig (1970). The data are averages (for six observers) for detection of one-dimensional sinusoidal signals in added two-dimensional white noise. Such a plot is an unnormalized inverse of the one-dimensional contrast sensitivity function. Note that as the root mean square noise level increases, the minimal shift to lower frequencies and the curves flatten.
They interpreted the parameter R as internal noise. The values of the parameters a and R varied with spatial frequency. They also measured the CSF with 1/f noise in the horizontal direction of the television scan lines. The noise would be uncorrelated (white) in the vertical direction so its influence is hard to interpret.
4.6 Two-Dimensional White-Noise Experiments
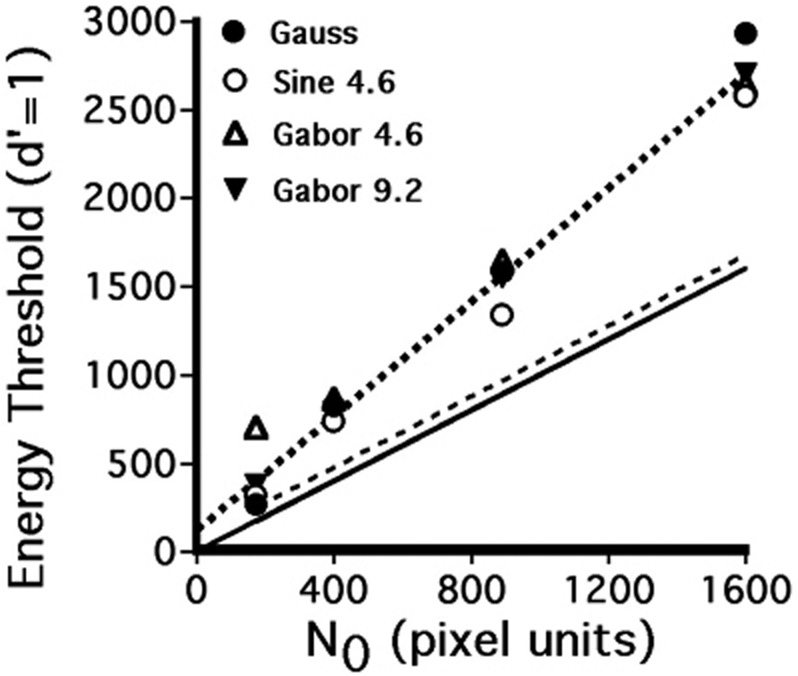
Research with 2D images only became possible with the advent of image “frame buffers” (now called display memory) in the 1970s. But they were very expensive at first. A 640 × 512 display system cost about $100,000 in 1980 ($270,000 in 2007 dollars), so very few university laboratories had one. Burgess et al. (1981) did the first investigations of decision efficiency with computer-generated grayscale images using a 640 × 512 system. We used uncorrelated Gaussian noise and demonstrated that humans could perform amplitude discrimination tasks with efficiencies well over 50% with sampling efficiencies as high as 80%. We used amplitude discrimination tasks because we had found in preliminary experiments that the detection psychometric function (d′ versus signal amplitude) was nonlinear at low amplitudes and the effect became increasingly important for sine-wave signals as spatial frequency increased. We found that for amplitude discrimination tasks the psychometric functions were both linear and proportional to signal amplitude. A discrimination threshold was defined as the signal energy required to obtain d′ equal to 1 (76% correct in a 2AFC task). Four signals (a compact 2D Gaussian disc, a 4.6 cycles/degree two-cycle sine wave, and two Gabor functions) were used and four noise spectral densities were used. The signal energy threshold results for amplitude discrimination as a function of image noise spectral density, N0, are shown in Figure 4.5.
Figure 4.5 A plot of energy threshold results for signal amplitude discrimination as a function of white-noise spectral density, N0, in comparable units. The human data are averages for three observers and 1,024 trials per observer per datum. The periodic signal frequencies (4.6 and 9.2) are given in cycles/degree. The solid line shows results expected for the ideal observer. The dashed line parallel to it includes additive internal noise. The dotted line through the human data has a slope of 1.61, indicating a sampling efficiency of 62%. The highest absolute discrimination efficiency in the plot is 59% (for the sine wave at N0 equal to 1,600). The highest sampling efficiency is 80% (for the 4.6 cycles/degree Gabor function).
Observer efficiencies depended on the noise spectral density. The highest values were about 50% obtained at the highest noise spectral density. For this spectral density the standard deviation of the image pixel noise was 15.6% of the 8-bit display range. We found efficiencies of about 50% for detection of aperiodic signals such as sharp-edged discs and compact 2D Gaussian functions. Efficiency for detecting sinusoidal signals was in the 10–25% range. The decrease in sinusoidal detection efficiency is probably due to an inability to make precise use of absolute phase information. A phase uncertainty (jitter) of as little as a quarter of a cycle dramatically reduces sine-wave detection accuracy. At the peak of the contrast sensitivity curve (roughly 4 cycles/degree), a quarter of a cycle corresponds to approximately the full width at half maximum of the optical point-spread function of the eye.
The fact that the regression lines through the observer data in Figure 4.5 do not pass through the origin indicates that observers have internal noise. It is not likely to be neural noise. The more probable explanation is that we cannot do mechanical calculations of likelihood ratios, which leads to noisy decision making. The fact that the regression lines are not parallel to the ideal observer line indicated that we do not do perfect sampling of the data. For example, our template may vary in size, shape, or position from trial to trial even though we are given complete information about the signal and its possible positions. These variations would introduce additional noise into the decision process, as discussed below.
The measures used in the above plot will now be discussed. White-noise digital images with a nominal sampling distance of unity have a Nyquist frequency of 0.5 and a two-sided spectral density, N0, equal to the pixel variance. The energy threshold concept arises as follows. The task is done under SKE and BKE conditions with white noise. Centered on a known location (x0, y0), let the image data be described by g(x − x0, y − y0) = As(x − x0, y − y0) + n(x − x0, y − y0) where the signal is described by As(x − x0, y − y0) and the white noise is described by n(x − x0, y − y0). The optimum ideal observer detection strategy on a trial-by-trial basis in a 2AFC task with white noise is to use the signal as a template, t(x, y), and cross-correlate it with the data at the potential signal locations, g(x − x0, y − y0) ⊗ t(x, y).
Recall that convolution of two functions in the space domain can be described by multiplication of their Fourier transforms in the frequency domain. When cross-correlation is done in the space domain, the Fourier domain multiplication involves the complex conjugate of one of the functions. So cross-correlation using the signal as a template can be described in the frequency domain as G(u, v)T∗(u, v) = A2S(u, v)S∗(u, v) + N(u, v)T∗(u, v), where * indicates the complex conjugate. The noise is white with spectral density N0 and statistics that are independent of location. The noise can be assumed to have zero mean without loss of generality. It can be shown using Equation (4.13) that d′, or equivalently the SNR for the ideal observer with white noise, is given by
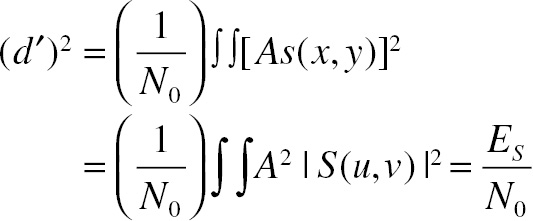 (4.13)
(4.13)The integral over the quadratic content of the signal is known as its energy, ES. One important observation is that for the ideal observer doing an SKE task, d′ will be proportional to signal amplitude. This is also true for all linear models of signal detection.
One point on terminology should be noted. In SDT-based work, signals are described by amplitude profiles rather than contrast. In radiology, the term “contrast” can have a number of meanings and therefore can be ambiguous. It is often calculated by normalizing the signal profile by the local image mean value, L0, in its vicinity. So the signal contrast profile is defined by c(x − x0, y − y0) = s(x − x0, y − y0)/L0. If the contrast representation is used for the signal, then it must also be used to normalize the noise fluctuations. Since N0 describes the squared noise fluctuations, the (L0)2 terms in both the numerator and denominator of the equation cancel. This is true for all model observers so there is no benefit obtained from using the contrast representation in SDT calculations. This is a useful property, since “contrast” values in digital images are arbitrary; they are determined by details of the display window and level settings.
After the brief Burgess et al. (1981) paper was published, we unsuccessfully submitted a much more detailed paper to another journal. The associate editor for vision (a physiologist) was not a fan of the application of linear systems theory or SDT to visual perception. The journal editor also suggested that, in spite of the high efficiencies, we had not demonstrated that humans could do cross-correlation detection. At the same time I had applied to the Medical Research Council of Canada for funding to continue the work. One of the grant reviewers took exception to the fact that I had ignored the autocorrelation theory of vision, which had been proposed in the early 1970s. An autocorrelator is an energy detector, which is not able to use sine-wave phase information, and therefore performs worse than a cross-correlator under SKE conditions. On the next submission of the grant, I discussed this point and got funded. However, because of the above objections, I undertook a program of investigations about human observer abilities: use of phase information for sine-wave detection and discrimination, detection in multiple-alternative locations, detection of Walsh–Hadamard signals with and without reference signals, and identification of these signals from an M-alternative menu. These investigations (all done using white noise) convincingly demonstrated that we performed better than the best possible autocorrelator and were consistent with the view that we were able to perform as suboptimal cross-correlators using a Bayesian decision strategy.
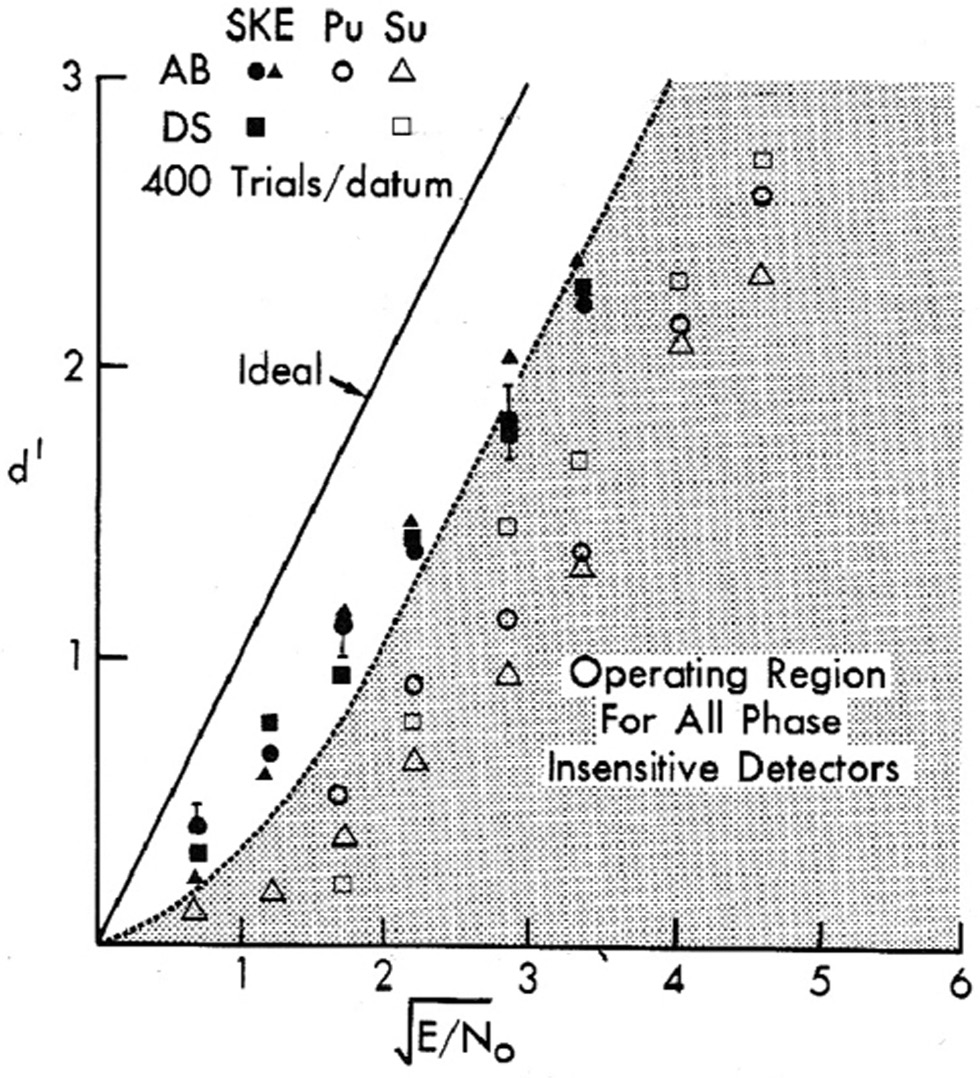
The sine-wave detection study by Burgess and Ghandeharian (1984a), was designed to determine whether we could do better than the best possible autocorrelator performance. The results are shown in Figure 4.6. Two human observers did experiments with three conditions. The first condition was based on a signal known exactly but variable (SKEV) paradigm. The profile of the two-cycle sine wave (4.6 cycles/degree) was made known to the observer but varied from trial to trial. In one case, the signal phase was selected randomly for each trial and the reference signal shown to the observer was simultaneously changed. In the other two conditions the signal was only defined statistically for the human observers (the SKS paradigm). In one case (points labeled PU), the observer was uncertain about signal phase because it varied randomly from trial to trial but the phase of the available reference signal never changed. In the final condition there was signal starting position uncertainty (points labeled SU). The performance of the autocorrelator was determined by Monte Carlo experiments. It is clear in Figure 4.6 that the human observers, under SKE conditions, do better than the best possible phase-insensitive detector for SNRs below about 2. There was another experiment involving discrimination of two-component sine-wave signals that also clearly demonstrated that we could use phase information. These phase experiments were the first steps in demonstrating that we can do Bayesian cross-correlation signal detection similar to the ideal observer.
Figure 4.6 Detectability of a two-cycle sine wave (4 cycles/degree) in white noise as a function of signal-to-noise ratio (square root (E/N0)). The shaded area indicates performance worse than the model observer that is ideal, except for the fact that it cannot use sine-wave phase information for detection (known as an autocorrelator). The data points are human results explained in the text. Note that humans do better than the autocorrelator for the signal-known-exactly (SKE) condition when the signal-to-noise ratio is below about 2.
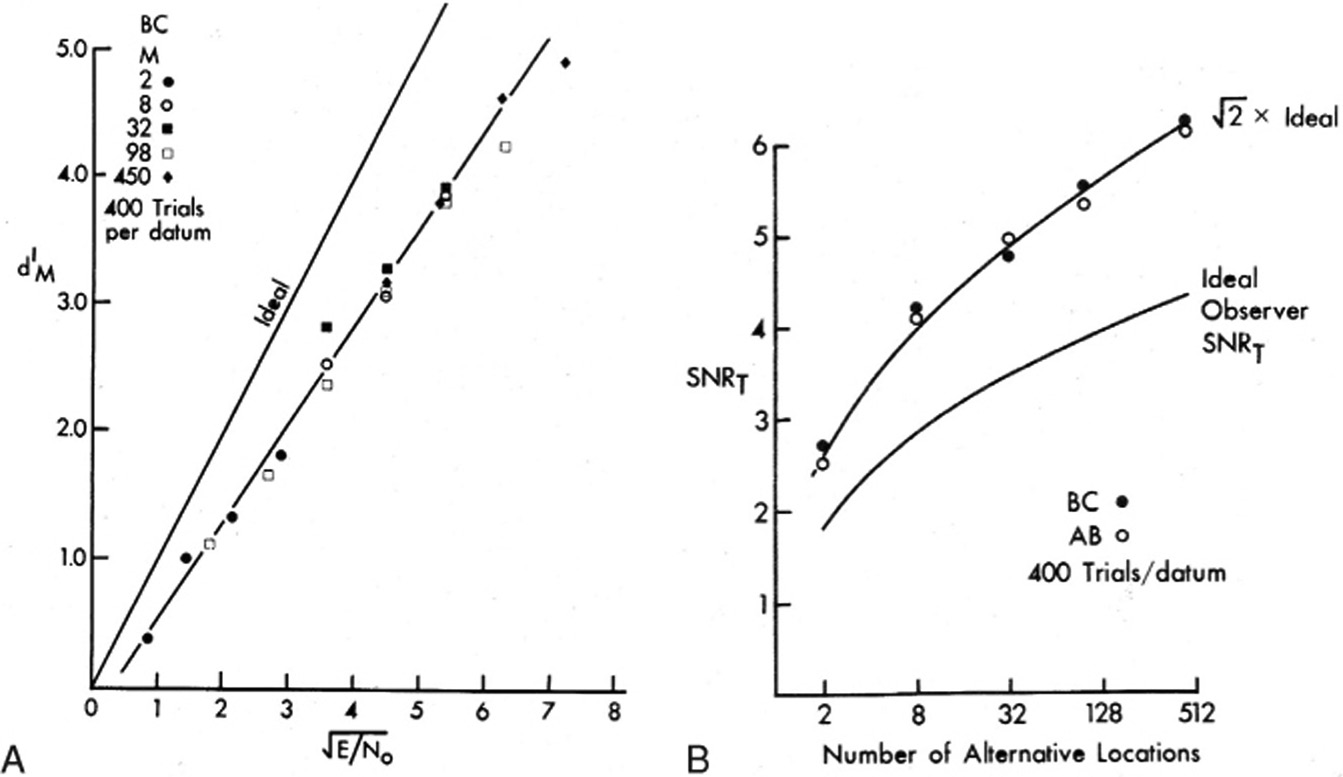
The second study by Burgess and Ghandeharian (1984b) was designed to see if human observer performance for signal detection with M-alternative and statistically independent locations could be predicted from 2AFC detection results using the standard SDT calculation. The additional locations gave additional opportunities for a noise-only location to yield a cross-correlation result that was higher than that obtained at the actual signal location. This effect could be accounted for using standard probability theory methods. This means that the value of d′ in an MAFC experiment depends on both SNR and the value of M. The signal was a disc (8-pixel diameter) in white noise. The number of locations ranged from 2 to 98. The results are shown in Figure 4.7. Part A of the figure shows the values of d′ (M) as a function of SNR. The fact that the data fall on a common line indicates that M-alternative results can be predicted from 2AFC results. There is also a small offset; the line does not go through the origin so human d′ results are not proportional to SNR. This feature is found in all human experiments. Two observers did this experiment but only the results for one are shown. Part B of the figure shows SNR threshold variation for 90% correct decisions as M increases. The human results all fall on a curve that is √2 higher than the ideal observer for all values of M. This is just another way of presenting the data in part A, but makes the point about performance prediction from SDT more clearly. The ratio of performances indicated that the human absolute efficiency is 50%. The results of this study indicate that humans are able to behave in a Bayesian manner, making use of prior knowledge about possible signal locations in a way that can be predicted by SDT.
Figure 4.7 Results for observer BC doing an M-alternative forced-choice disc signal location identification experiment. (A) d′ dependence of signal-to-noise ratio (SNR) and the value of M. Note that the equation relating d′ and SNR depends on the value of M. (B) SNR thresholds (for 90% correct detection) as a function of M for both human observers and the ideal observer. The curve that is √2 higher than ideal observer data shows that the humans are maintaining 50% detection efficiency as M varies.
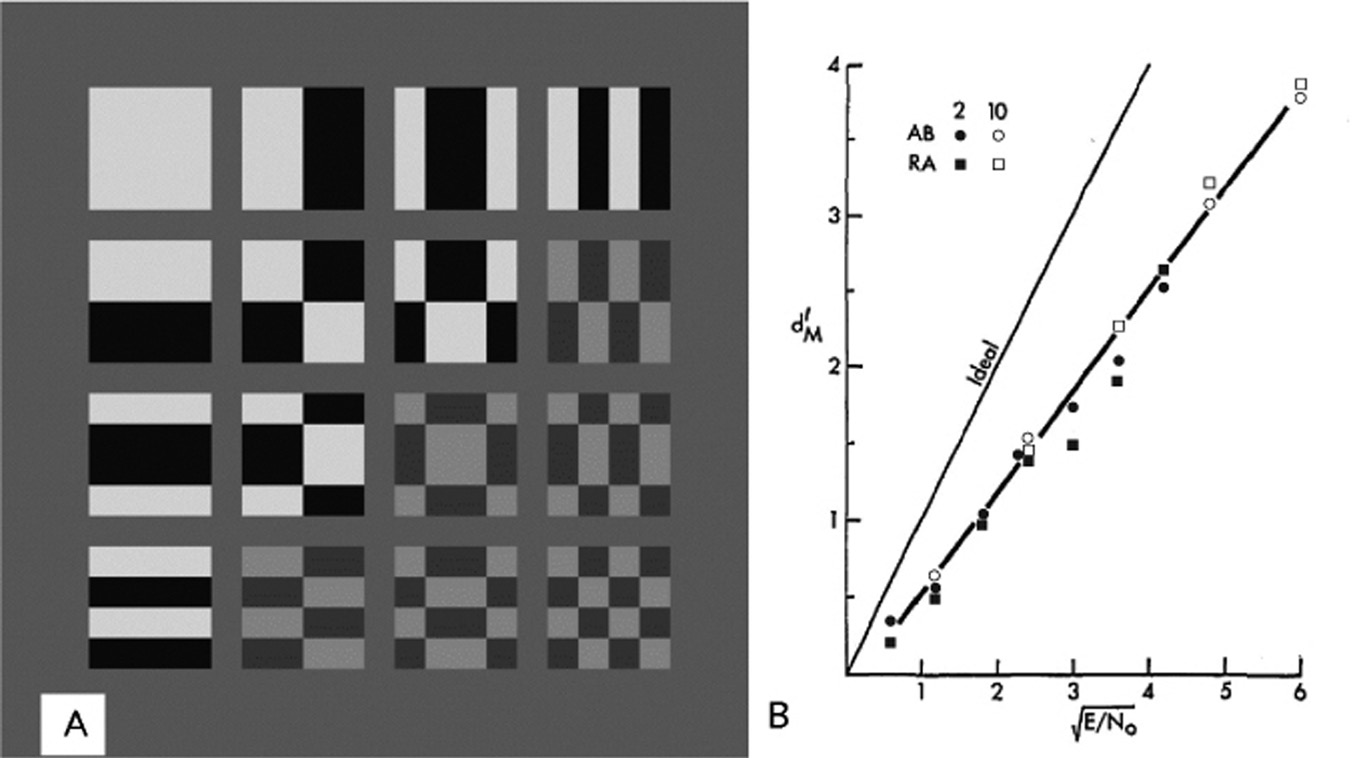
The third study by Burgess (1985) was also based on the Bayesian use of prior knowledge issue. The signal set was a collection of 2D Walsh–Hadamard functions, which are checker-board-like, as shown in Figure 4.8. The functions are orthogonal so alternative decisions are statistically independent. A number of experiments were done but only two will be discussed here. One experiment was 2AFC detection using an SKE but variable paradigm. The signal was randomly selected from the ten highlighted choices in part A of the figure and a reference version was shown to the observer during the decision trial. The second experiment was M-alternative signal identification. One signal was randomly selected from the set and the observer’s task was to identify the signal and indicate his or her choice using the reference menu of all possibilities.
Figure 4.8 (A) The task was either two-alternative forced-choice (2AFC) detection (signal-known-exactly) of one of the ten highlighted Walsh–Hadamard functions, or M-alternative forced-choice (MAFC) identification of which signal was present from a menu of the ten. The results are shown in part B. The MAFC identification results could be predicted from the 2AFC results using the standard signal detection theory calculation.
Human efficiencies were consistently high for all three studies: about 50% for detection of simple aperiodic signals, about 35% for Walsh–Hadamard signal detection and identification, and in the vicinity of 10–25% for SKE detection of sine waves. The results of the series of studies presented clear evidence that our ability to do signal detection tasks in white noise could be described by an observer model that could do cross-correlation detection and make use of prior information in the manner that a Bayesian decision maker would. Our performance efficiency was not 100%, but 50% for a simple task is quite good.
The final experiments in this series, by Burgess and Colborne (1988), were designed to study one possible source of inefficiency – internal noise. This was done in two ways. In the first method (two-pass), observers viewed the sequence of 2AFC image pairs twice with an interval of many weeks between observation trials. The signal would be in the same field in identical pairs of noise fields each time. This method allowed for analysis of observer consistency – a mechanical observer with no data acquisition or decision noise would make identical decisions on the two viewings of the image pairs. Note that the mechanical observer need not be ideal. An estimate of observer internal noise could be obtained using the probability of correct response and the probability of decision agreement. The second method was based on twinned noise. The noise fields for the two alternatives were identical. The mechanical observer would subtract the two image fields and the signal would be revealed in a noiseless background 100% of the time.
A second experiment was then done using different noise backgrounds in the two alternative images. Relative performance results for the two cases could be analyzed to yield estimates of internal noise. All experiments were done using the four-image white-noise variances shown in Figure 4.5.
The results were surprising. We found that there were two noise components. The first was the internal noise indicated by the nonzero intercept in Figure 4.5. This was independent of the noise level in the displayed images and was referred to as static noise with spectral density, Ns. The value of the static noise spectral density can be estimated using the intercept of the regression lines with the abscissa in Figure 4.5. The other noise component had a variance that was proportional to the variance of the image noise (with a constant fraction of about 64%). Since this component depended on noise in the image, it was referred to as induced noise. When image noise is white with spectral density, N0, this induced noise can be included in observer models by using an effective image noise spectral density, Neff = (1 + ρ2)N0, where ρ2 equals 0.64. This means that observer absolute efficiency will be at most about 60%. This is consistent with a number of results. A simple model for human performance with white noise can be obtained by modifying the ideal observer equation (Equation 4.13), to include these two sources of internal noise. The result is
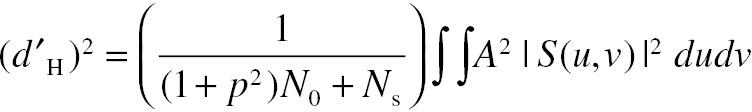 (4.14)
(4.14)Another point about this induced internal noise component is that it influences the slope of the regression line in Figure 4.5. Induced internal noise cannot be distinguished from suboptimal sampling efficiency on the basis of experiments to the date of this investigation (Burgess and Colborne, 1988). In fact, induced noise and suboptimal sampling may actually be two ways of talking about the same phenomenon – inconsistent use of a template for image data collection. The topic of induced noise would be revisited about a decade later using both low-pass and high-pass noise (Burgess, 1998). This will be discussed below.
Researchers in spatial vision research also began to use noise-limited images and observer efficiency to investigate human performance. Pelli (1981, 1985) used 1D sine waves in noise to measure observer efficiency as a function of noise spectral density. He interpreted the nonlinear psychometric function for detection as an indication of channel uncertainty. As the price of 2D image display systems dropped dramatically in the 1980s, vision scientists also began to investigate noise-limited detection of more complex signals. These included 2D spatial sine-wave detection by Kersten (1983), detection of 2D visual noise by Kersten (1986), American Sign Language communication by Pavel et al. (1987), recognition of 3D objects in noise by Tjan et al. (1995), discrimination of fractal images by Knill et al. (1990), and estimation of fractal dimension. Geisler and collaborators in 1985 began an extensive program of investigations using the ideal observer concept in order to evaluate mechanisms through stages of the visual system. Geisler (2003) describes their work, which is based on the idea of introducing known properties of the visual system as constraints to the ideal observer and then comparing human and ideal performance of detection, discrimination, and identification tasks subject to these constraints. Geisler referred to this as sequential ideal observer analysis.
4.7 Estimation of Observer Templates
The high human observer efficiencies for decision tasks with white noise suggest that we are able to do a reasonably good job of matched filtering. That is to say, we are able to effectively use the signal (under SKE conditions) as a template. This requires that the template not only has the correct functional profile, but during a large number of decision trials it must be consistently of the correct size and it must be consistently placed in each of the possible signal locations. It would be nice if we had a more direct method of estimating the template used by the observer.
Classification image analysis provides such a method. The basic idea of the method is to take the average difference (over a large number of trials) between the image chosen in a 2AFC trial (whether it is a correct choice or not) and the image that is not chosen. The method was first used in audition research because signals and noise for decision trials could be recorded and replayed (Ahumada and Lovell, 1971). For white noise, this average can be computed analytically. A transformation of the average result provides an estimate of the linear template used by the observer.
Abbey et al. (1999) described the theoretical background of the method. They did Monte Carlo validation experiments (10,000 trials) using a 2D Gaussian signal and a model (nonprewhitening with an eye filter (NPWE)) observer applying a known template to the images. They then did preliminary human observer experiments (two observers and 2000 trials each after 840 training trials). There was very good agreement between estimated human and NPWE templates. For the human experiments, the results are easiest to explain using the filters obtained by Fourier transformation of the templates. At low frequencies the human filter fell in between those expected for an ideal observer (using the signal as a template) and the NPWE observer model. The human filter results extended to higher frequencies than expected for either observer model – suggesting that the human observers were incorporating some spatial frequencies with little or no signal content into their observer templates.
The mathematical derivation of the method is somewhat involved so it will only be outlined here. Let the signal be described by the vector, s, in white noise described by the vector, n, added to a known background described by the vector, b, added together to create an image, g. The observer is assumed to use a template described by the vector, w. The observer’s internal responses, λ, included internal noise, a Gaussian random sample value for each trial, ε. Using the superscripts + and – to indicate the images with the signal present and absent, the images and the observer’s internal responses are given by
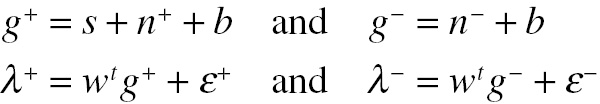 (4.15)
(4.15)The same deterministic background is used in both images so it disappears when differences are calculated. However, the method can be extended to include stochastic backgrounds. The human observer’s internal response cannot be observed, but the observer’s score, o, on a given trial, j, can be used as a surrogate, giving o = step(λ+ − λ−), where o = 1 if the decision is correct and o = 0 if the decision is incorrect. The probability of correct response for N trials is the mean (expectation) value PC = E(o). Let σ be the standard deviation of the white noise and ∆ n be the difference between the noise vectors for the two images in a 2AFC trial, (n+ − n−). Then the classification image estimate, E(∆ q), can be described by
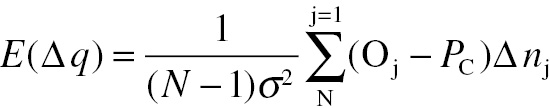 (4.16)
(4.16)This classification image is used as an estimate of the template used by the observer. It should be noted that a very large number (many thousands) of 2AFC decision trials are needed to obtain a reliable estimate.
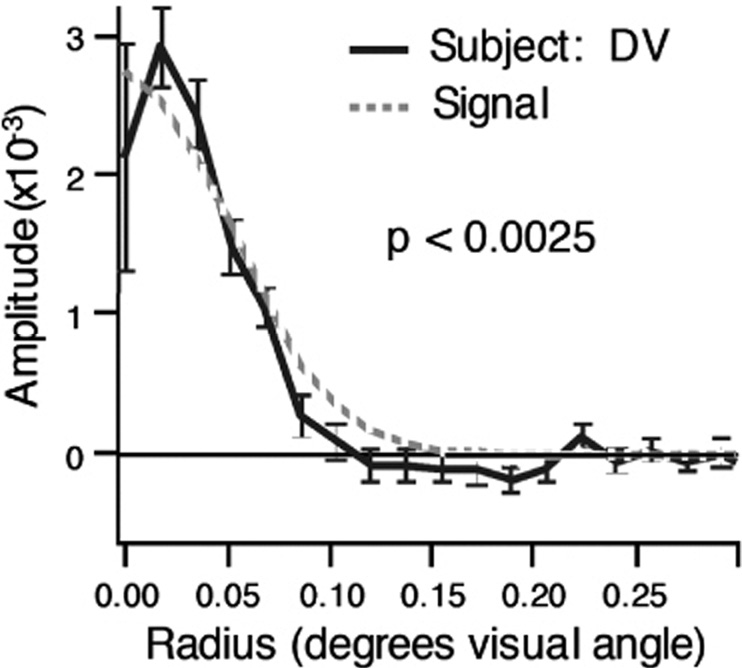
Abbey and Eckstein (2002) used this method to estimate the templates used by two very experienced observers during 2AFC detection of a Gaussian signal. The results obtained for one observer are shown in Figure 4.9. They found that the classification image estimates were isotropic, so they averaged over angle. To reduce the noise in the results, the data were binned by radial visual angle. The estimates at small angle have larger errors because fewer angular values were available for averaging. The scaled template (the signal) that would be used by the ideal observer is overlaid on the human data. There is reasonably good agreement between the human and ideal templates except that the humans present a negative amplitude over one range of radial distance. They suggested that this indicates the possibility of an inhibitory surround in the template (this is consistent with the low-frequency drop in the human CSF used in the NPWE model).
Figure 4.9 Radial average of the observer template estimate for one very well-trained observer. The radial profile of the signal is also plotted. The error bars are 1 se for averages in each radial distance bin.
Abbey and Eckstein (2006) investigated the template used for three 2AFC tasks in Gaussian white noise. The first was detection of a difference of Gaussians (DoG) signal. The second task was discrimination between DoG signals that were identical except for contrast – the different signal for this task is also a DoG signal with the same spatial form. The third task was identification (actually form discrimination) between two DoG signals of different spatial extent, selected so that the different signal was also a DoG signal with the same spatial form as that present for the other two tasks. The ideal observer would use the same DoG filter to perform all three tasks. They selected the DoG signal because it has a band-pass profile in the spatial-frequency domain. They could tune the signal to be detected to spatial frequencies of interest by adjusting the DoG parameters. They selected a peak spectral amplitude at about 4 cycles/degree and a bandwidth (full-width at half-maximum) of approximately 1.8 octaves.
The observers’ classification of images across the three tasks were significantly different. Greatest variability appeared to be at low spatial frequencies (less than 5 cycles/degree). In this range they found frequency enhancement in the detection task, and frequency suppression and reversal in the contrast discrimination task. In the identification task, observer template estimates agreed reasonably well with the ideal observer template.
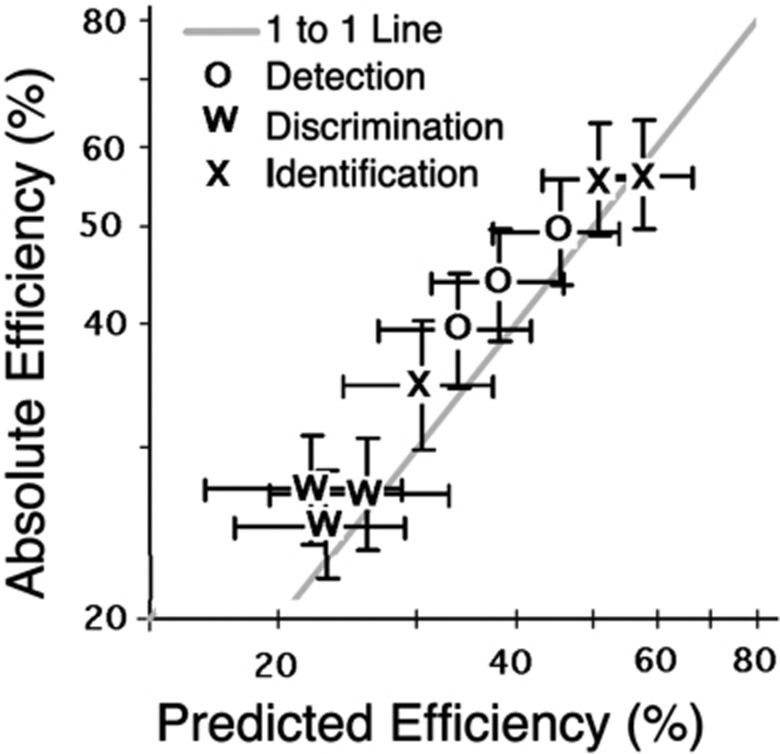
They evaluated the effects of hypotheses of a nonlinear transducer and intrinsic spatial uncertainty as explanations of the human observer divergence from the ideal observer results. They found that the variation in classification images that they obtained for the human observers could not be explained as a transducer effect alone. They found that the effects of nonlinear spatial uncertainty could act as a mechanism for low-frequency enhancement of the classification images for the detection task. However, none of the models investigated fully explained the observed human data. They compared the human observer efficiencies that were calculated from the percentage of correct responses with the efficiency determined on the basis of estimated linear templates of the three observers. The results are shown in Figure 4.10.
Figure 4.10 A comparison of human observer efficiencies that were calculated by Abbey and Eckstein (2006). The absolute efficiencies were determined from the percentage of correct responses and the predicted efficiency was determined in a Monte Carlo experiment using the individual estimated linear templates of the three observers. The error bars are 95% confidence limits.
4.8 Can we Prewhiten?
4.8.1 Matched Filters
In the late 1980s, visual signal detection research shifted to the issue of trying to understand how the form of the random noise power spectrum affects human signal detection performance. When the image noise (or stochastic background fluctuations) is spatially correlated, there are two main classes of models that we use in medical imaging. One is based on the ideal PW matched filter strategy while the other class is based on suboptimal NPW matched filters (Wagner and Weaver, 1972). The PW model is an observer that is able to modify its template (or filter) to compensate for correlations in the noise – a process known as PW. The NPW model in an observer is unable to modify its template (or filter) to prewhiten correlated noise. The PW and NPW models are obviously identical for white noise and uniform backgrounds.
As will be seen later, the NPW model does very poorly for stochastic (spatially varying) backgrounds. The problem arises because the model uses the signal as a template for cross-correlating and local variations in background are included in the decision variable. This problem can be overcome by using a template with an antagonistic center-surround structure similar to retinal receptive fields so that there is (on average) zero response to local background variations. The Fourier transform of the appropriate template will be zero at zero spatial frequency (“DC”). This can be achieved by multiplying the signal amplitude spectrum by an eye filter with a “zero DC value.” One isotropic form could be E(f) = fb exp(−cf), where f is radial frequency, and b and c are adjustable parameters. This modified model is referred to as the NPWE, which was first proposed by Ishida et al. (1984). The models are discussed in detail in Chapter 18.
The SNR (or d) equations for the models performing an SKE/BKE task will now be discussed. The imaging system modulation transfer function (MTF) will not be included for simplicity. Assume that the signal to be detected has amplitude spectrum S(u, v). Assume that the colored noise has a power spectrum N(u, v). Then the SNR equations are given by
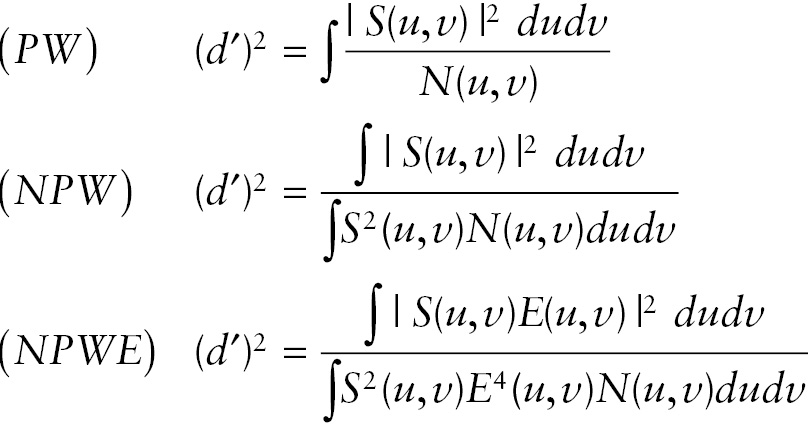 (4.17)
(4.17)With reference to Equation (4.18), the relationship between the PW and NPW models is illustrated as follows. Suppose the model observer performs detection by cross-correlating the image data with an arbitrary template, t(x, y), which has Fourier transform, T(u, v). The signal may not be symmetrical so one must be careful about the distinction between cross-correlation and convolution. In the space domain convolution integral, a reversed version of the template function is used. In the Fourier domain, one uses the product S(u, v)T(u, v). In the space domain cross-correlation integral, the template function is not reversed. In the Fourier domain, one uses the product S(u, v)T∗(u, v). The Fourier domain SNR (or d) integral calculation goes as follows. The first integral gives the (d)2 result for the filter corresponding to the arbitrary template. The second line (NPW) shows what happens if the observer is not ideal and uses the signal as a template. The third line shows what happens if the PW matched filter, TMF(f) = αS∗(u, v)/N(u, v), is used:
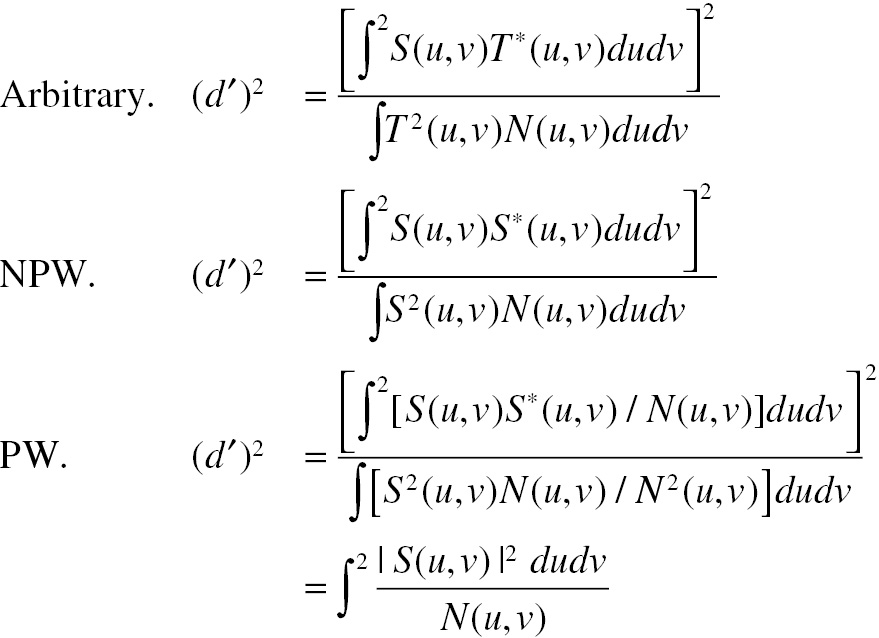 (4.18)
(4.18)Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree