16.1 Introduction to Multireader ROC Analysis
Receiver operating characteristic (ROC) analysis is a well-established method for evaluating and comparing the performance of diagnostic tests or imaging modalities, as discussed in Chapter 15. ROC curves allow us to quantify the ability of a reader to discriminate between diseased and normal cases in a way that does not depend on the thresholds used by the reader. Throughout this chapter we assume that we are considering diagnostic imaging studies where there are multiple readers (e.g., radiologists) who assign to each case (i.e., patient) a disease severity or disease likelihood rating based on the corresponding image or set of images, acquired using one or more imaging modalities. The readers are asked to use either a discrete (e.g., 1, 2, 3, 4, or 5) or a quasicontinuous (e.g., 0–100) ordinal rating scale. From these ratings, ROC curves and corresponding accuracy estimates are computed for each reader and each modality (if there are multiple modalities), in order to assess reader performance for each modality.
In imaging studies, there typically exists variation in ratings due to readers. For example, for a disease such as breast cancer, the rating assigned to a case can be different for two radiologists, even if they have similar experience and training. In such situations we say there is reader variability. When human readers are involved in evaluating images, either unaided or using computer-aided diagnosis (CAD), then the assumption of no reader variability is typically not realistic.
The methods discussed in Chapter 15 only take into account variation in ratings due to subject variability when making inferences (e.g., computing p-values and confidence intervals); hence these methods are limited either to studies where there is no reader variability, or where the researcher is only interested in the performance of the modalities when used by the particular reader or readers in the study. An example where there is no reader variability is when the scoring of an image is completely done by a computer technology; for this situation there is no reader (i.e., computer) variability, and thus the methods from Chapter 15 would be suitable for such a study.
For studies where there is reader variability, the researcher typically will prefer to have conclusions apply to both the reader and case populations. For example, in comparing modality A with modality B, the conclusion “modality A performs better than modality B, taking into account both reader and case variability” is typically preferable to the conclusion “modality A performs better than modality B when images are read by the five radiologists used in the study.” The second conclusion is restricted to the readers used in the study; in contrast, the first conclusion applies to the population of readers from which the study readers can be treated as a random sample. Although an extension of the methods in Chapter 15 can yield a conclusion such as the second one, they cannot yield a conclusion like the first.
The purpose of this chapter is to provide an introduction to the analysis of multireader ROC data that takes into account reader variability. The remainder of the chapter is organized as follows. In section 16.2 I discuss an example of a multireader study where the researcher wants to account for reader variability. I describe the major approach for multireader ROC analysis that accounts for reader variability in section 16.3, and illustrate its use for section 16.2 example in section 16.4. In section 16.5, I discuss computing sample size estimates for planned multireader studies. Concluding remarks are made in section 16.6.
16.2 Example: Spin-Echo Versus Cine MRI
In this section, I consider a motivating example. The data for the example consist of rating data for a study where several radiologists read the same set of images. The researcher wants to compare two modalities and wants conclusions about the modalities to apply to both the reader and case populations. Methods that accomplish this goal are commonly referred to as multireader multicase (MRMC) methods, and data for which these methods are designed are referred to as MRMC data. In section 16.3 I discuss the most popular MRMC analysis methods.
The data are provided by Carolyn Van Dyke, MD. The study (Van Dyke et al., 1993) compared the relative performance of single spin-echo (SE) magnetic resonance imaging (MRI) to cine MRI for the detection of thoracic aortic dissection. There were 114 patients – 45 patients with an aortic dissection and 69 patients without a dissection – imaged with both SE and cine MRI. Five radiologists independently interpreted all of the images using a five-point ordinal scale: 1 = definitely no aortic dissection; 2 = probably no aortic dissection; 3 = unsure about aortic dissection; 4 = probably aortic dissection; and 5 = definitely aortic dissection. Each radiologist read each image using each of the two modalities, SE and cine MRI. Because each reader read each image under each modality, this study has a factorial design with three factors: modality, reader, and case.
The performance of the two modalities can be compared descriptively by visually comparing plots of the ROC curves that show the performance of the modalities for each reader. Two common methods for computing the ROC curve are: (1) the nonparametric or empirical method, where the ROC curve is constructed by connecting the observed (1 – specificity, sensitivity) points (computed by treating each discrete rating as a threshold) with straight lines; and (2) the semiparametric method, which assumes that the discrete ratings reported by a reader, as required by a study, represent the “binning” of latent (i.e., unobserved) values of a continuous decision (i.e., rating) variable that follows a particular parametric model. Often the binormal model, discussed in Chapter 15, is assumed to model the latent continuous decision variable when using the semiparametric method. Typically, the semiparametric method estimates the ROC curve using maximum-likelihood estimation, resulting in a smooth ROC line.
The nonparametric ROC curves are presented in Figure 16.1 and the semiparametric ROC curves, assuming a latent binormal model, in Figure 16.2. In both figures we see that the ROC curve for SE MRI tends to be above that for cine MRI for each reader (except for the semiparametric curves for reader 3, which look very similar), suggesting that SE MRI performs better.
Figure 16.1 Observed (1 – specificity, sensitivity) points and nonparametric receiver operating characteristic curves for spin-echo and cine magnetic resonance imaging in the detection of aortic dissection.
Figure 16.2 Observed (1 – specificity, sensitivity) points and binormal semiparametric receiver operating characteristic curves for spin-echo and cine magnetic resonance imaging in the detection of aortic dissection.
In addition to visually comparing ROC curves, we can compare reader performance outcomes, computed from the ROC curves, which describe the discriminatory ability for each modality and reader pair. A commonly used reader performance outcome is the area under the ROC curve (AUC), which was previously discussed in Chapter 15. This measure has the interpretation of being the probability that the reader will assign a higher rating to a diseased case image compared to a normal case image, plus one-half the probability of assigning tied ratings (Bamber, 1975; Hanley and McNeil, 1982). Table 16.1 presents the AUC accuracy estimates computed from the nonparametric and semiparametric ROC curves. From Table 16.1 we see that the two methods give similar but slightly different results, with the nonparametric method showing an AUC difference (SE – cine) of 0.941 – 0.897 = 0.044, averaged across readers, and the semiparametric method showing an average difference of 0.952 – 0.911 = 0.041, again suggesting that SE MRI performs better.
Table 16.1 Area under the curve estimates by reader and modality based on the nonparametric and binormal semiparametric receiver operating characteristic curves
| Estimation method | Modality | Reader | Mean | ||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |||
| Nonparametric | Cine | 0.920 | 0.859 | 0.904 | 0.973 | 0.830 | 0.897 |
| Spin echo | 0.948 | 0.905 | 0.922 | 0.999 | 0.930 | 0.941 | |
| Semiparametric | Cine | 0.933 | 0.890 | 0.929 | 0.970 | 0.833 | 0.911 |
| Spin echo | 0.951 | 0.935 | 0.928 | 1.000 | 0.945 | 0.952 | |
Another accuracy measure is the partial area under the ROC curve (pAUC), as discussed in Chapter 15. This is the AUC for a specified range of the false-positive fraction (FPF), or equivalently, for 1 – specificity. For example, if the researcher wants each modality to have a specificity of > 0.8 (or equivalently, FPF < 0.2), then it makes sense to compare modalities using the pAUC for 0 < FPF < 0.2. Table 16.2 presents the pAUC (0 < FPF < 0.2) for each reader–modality pair, computed from the nonparametric and semiparametric ROC curves. In Table 16.2 the pAUCs have been normalized by dividing by the FPF range of 0.2; the normalized pAUC can be interpreted as the average sensitivity over the restricted FPF interval (Jiang et al., 1996; McClish, 1989). From Table 16.2 we see that the two methods give similar results, with the nonparametric method showing an average pAUC difference (SE – cine) of 0.849 – 0.764 = 0.085 and the semiparametric method showing an average difference of 0.880 – 0.790 = 0.090, again suggesting that SE MRI performs better.
Table 16.2 Partial area under the curve (pAUC)C) estimates (0 ≤ false-positive fraction (FPF) ≤ 0.2) by reader and modality based on the nonparametric and binormal semiparametric receiver operating characteristic curves
| Estimation method | Modality | Reader | Mean | ||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |||
| Nonparametric | Cine | 0.808 | 0.703 | 0.735 | 0.945 | 0.629 | 0.764 |
| Spin echo | 0.831 | 0.805 | 0.794 | 0.997 | 0.818 | 0.849 | |
| Semiparametric | Cine | 0.822 | 0.726 | 0.794 | 0.949 | 0.658 | 0.790 |
| Spin echo | 0.868 | 0.843 | 0.820 | 1.000 | 0.869 | 0.880 | |
Note: the pAUC values have been normalized by dividing by 0.2, the FPF range. Thus the pAUC is the average sensitivity over the interval (0 < FPF < 0.20).
In this example the outcomes of interest are the ten reader performance estimates corresponding to the five readers and two modalities. That is, the outcomes are either the ten AUC estimates or the ten pAUC estimates, which we denote by AUCij or pAUCij, where i denotes modality and j denotes reader, with i = 1, 2 and j = 1, 2, 3, 4, or 5. Each of these accuracy estimates is computed from the 114 ratings corresponding to the particular reader and modality.
16.3 Multireader Multicase Methods
For our example there are 1140 ratings, 114 for each of the ten modality–reader combinations. However, for our analysis we are only interested in comparing the two modality mean accuracy estimates, resulting from averaging the accuracy estimates (the AUCs or pAUCs) across readers for each modality. Because each reader reads each image under each modality, the ten accuracy estimates are correlated with each other. This correlation must be taken into account when making inferences, e.g., when computing p-values for hypotheses tests or constructing confidence intervals.
The two conventional ways to account for correlated data are random effects models and generalized estimating equations (Zeger and Liang, 1986). For our example neither of these approaches works: the conventional random effects analysis of variance (ANOVA) model is not appropriate because the accuracy measure is not the mean of the case-level ratings, and generalized estimating equations are not applicable because there are no independent clusters of outcomes.
In this section, I give an introduction to the main MRMC methods. While some of the details require basic knowledge of ANOVA methods, it is not necessary to understand the details of this section in order to use the results. Thus I recommend that you skim over those statistical details that you may not have the necessary statistical background to understand.
16.3.1 The Dorfman–Berbaum–Metz (DBM) Method
The first practical way to analyze MRMC data was the procedure proposed by Dorfman, Berbaum, and Metz (DBM) (Dorfman et al., 1992); this method is commonly referred to as the DBM method. This method involves computing jackknife pseudovalues (Shao and Dongshen, 1995) and then applying a conventional random-effects ANOVA to the pseudovalues.
Jackknife pseudovalues are computed by leaving out one case at a time, computing the resulting accuracy estimate, then computing a weighted difference between the accuracy estimate based on all of the data and the accuracy estimate computed with the case omitted. Specifically, for modality i and reader j, the AUC pseudovalue for case k, denoted by Yijk, is defined by
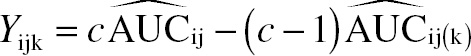(16.1)where AUC^ij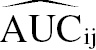
is the AUC estimate for modality i and reader j, computed from all of the data, AUC^ij(k)
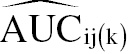is the AUC estimate computed from the same data but with data for case k removed, and c is the number of cases. Pseudovalues for pAUC are similarly defined. For our example there will be 1140 computed pseudovalues, one for each modality, reader, and case combination.
A random-effects ANOVA is then applied to the pseudovalues, treating pseudovalue as the dependent variable. For this ANOVA there are three factors: modality, reader, and case. Two-way and three-way interactions are included in the model. Modality is treated as a fixed factor because we are only interested in the modalities in the experiment. Reader and case are treated as random factors because we are interested in comparing the modalities for the populations of readers and cases. That is, we are interested to know what the expected difference in the modality accuracy measures is for a randomly selected reader reading images from randomly selected cases. A typical shorthand notation for this model that shows the effects in the model, with * used to indicate an interaction, is given by
Here and elsewhere I use treatment synonymously with modality for consistency with the computer output that will be presented and discussed in section 16.4.
Although the original DBM method performed satisfactorily in simulations, there were some problems with it: (1) it was limited to jackknife accuracy estimates (e.g., the jackknife AUC estimate); (2) it was substantially conservative (i.e., it accepted the null hypothesis too often and confidence intervals were too wide); and (3) it lacked a firm statistical foundation, since pseudovalues are not observed outcomes. Problem (1) was remedied by using normalized pseudovalues (Hillis et al., 2005a). Normalized pseudovalues are the same as raw pseudovalues, defined by Equation 16.1, except that a normalizing constant is added to the pseudovalues for each modality–reader pair so that the mean of the pseudovalues will be equal to the accuracy estimate. Problem (2) was remedied by using less data-based model reduction (Hillis and Berbaum, 2005) and a new denominator degrees of freedom (Hillis, 2007). The remedy for problem (3) will be discussed in section 16.3.3.
16.3.2 The Obuchowski–Rockette (OR) Method
Recall that the DBM method performs a conventional three-factor ANOVA of the pseudovalues. The three factors are modality (fixed), reader (random), and case (random). For our example there would be 1140 pseudovalues, one for each modality.
A seemingly different approach was suggested by Obuchowski and Rockette (OR) (Obuchowski and Rockette, 1995a), which we refer to as the OR method. Their approach applies an unconventional two-factor ANOVA to the outcomes of interest, the accuracy measure estimates; for our example these would be the ten accuracy estimates (AUCs or pAUCs), one for each modality–reader combination. The factors for the OR ANOVA are modality (fixed) and reader (random). Using shorthand notation the OR model, with AUC as the accuracy estimate, is given by
What is unconventional about the OR model is that the error terms are allowed to be correlated to account for the correlation due to each reader reading the same cases. The OR procedure defines the following three error covariances that are allowed to be different: (1) Cov1 is the covariance between error terms for the same reader using different modalities; (2) Cov2 is the covariance between error terms for two different readers using the same modality; and (3) Cov3 is the covariance between error terms for two different readers using different modalities. If this was a conventional ANOVA model, the errors would be assumed to be uncorrelated and thus there would be no covariance (i.e., zero covariance) between the error terms.
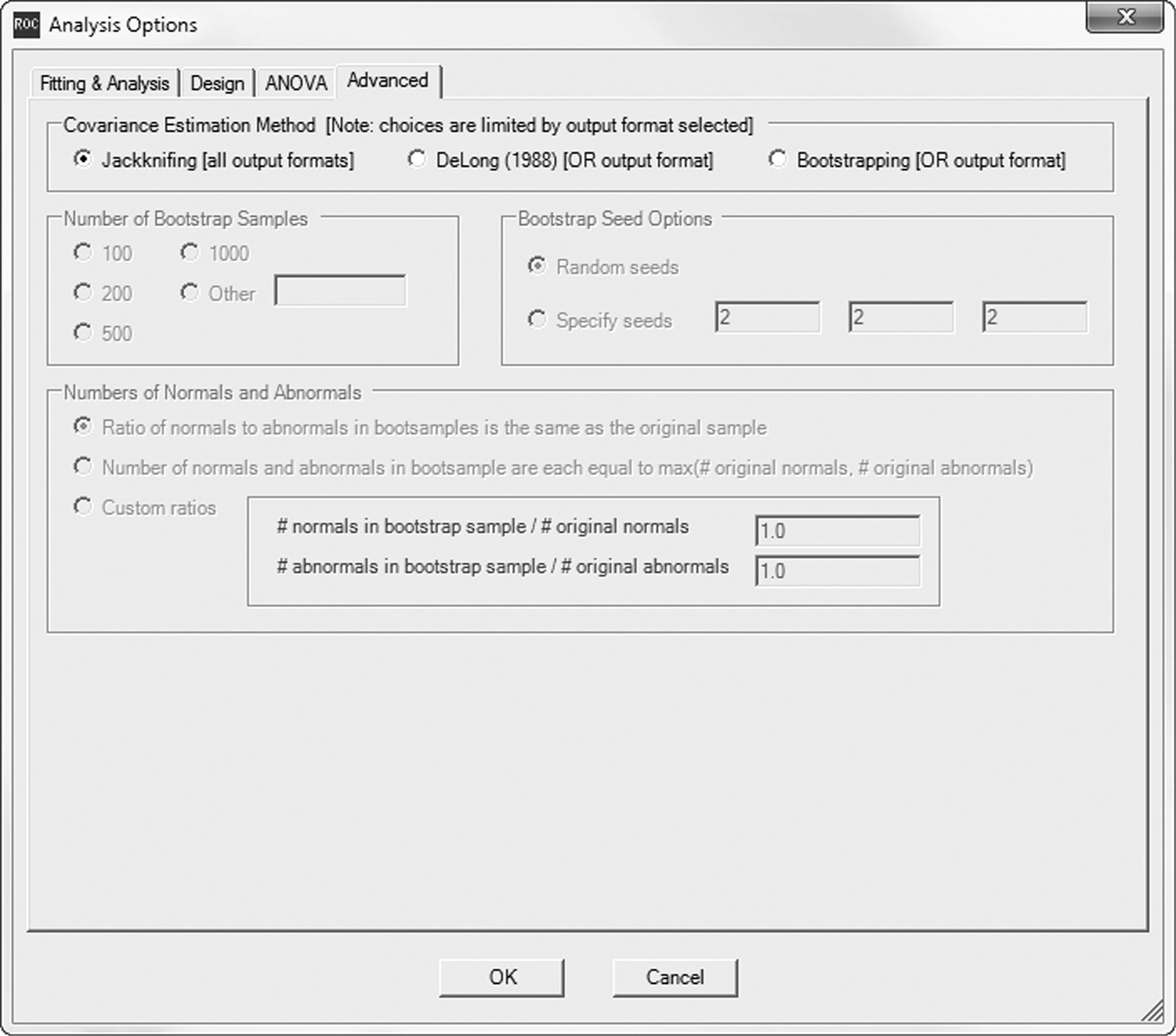
In the OR procedure these error term covariances are estimated using methods such as jackknifing, bootstrapping (Shao and Dongshen, 1995), and the method proposed by DeLong et al. (1988). The OR test statistic is similar to that obtained from a conventional ANOVA that treats the errors as uncorrelated, but it contains a correction factor in the denominator that is a function of the error covariance estimates. For this reason this method is sometimes referred to as the corrected F method. Specifically, if this was a conventional ANOVA model with independent errors, the F statistic for testing for a modality difference would be
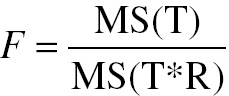
where MS(T) is the mean square due to treatment (i.e., modality) and MS(T*R) is the mean square due to the treatment-by-reader interaction. In contrast, the OR procedure uses the following statistic:
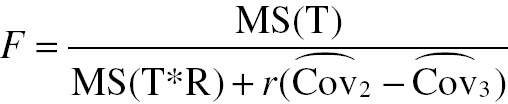
Here Cov^2
and Cov^3
are estimates of the corresponding covariances and r is the number of readers. Note that this F statistic differs from the conventional ANOVA F statistic only in the addition of the “correction” factor, r(Cov^2−Cov^3)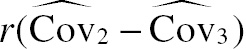
, in the denominator.
An advantage of the OR procedure, compared to the DBM procedure, is that it is based on a firm statistical model. However, a disadvantage for the OR procedure, as originally presented, was that it did not perform as well as the DBM procedure. Specifically, it tended to be even more conservative than the DBM procedure, especially when the number of readers was small, as is often the case for imaging studies.
16.3.3 Relationship Between DBM and OR
For more than 10 years the DBM and OR procedures were considered to be different procedures, which is understandable since they appear to be quite different in their original formulations. However, it was shown that the two procedures are closely related when Hillis et al. (2005) showed that the modified DBM method that uses normalized pseudovalues and less data-based model reduction yields the same F statistic as OR, if OR uses jackknife covariance estimates. Furthermore, they showed that if OR does not use jackknife covariance estimates (e.g., it uses bootstrapping or DeLong’s method), the same F statistic can still be obtained using DBM with quasi pseudovalues (which I will not try to define in this chapter). However, the two methods still gave different results because they used different denominator degrees of freedom (ddf) formulas. This discrepancy was resolved by a new ddf formula (Hillis, 2007) that could be used with both procedures, improved the performance of both procedures, and made the procedures equivalent (since they have the same F statistic and the same ddf).
Thus the updated DBM procedure can be viewed as equivalent to the updated OR procedure. (The updated DBM procedure uses normalized or quasi pseudovalues, less data-based model reduction, and the new ddf; the updated OR procedure uses the new ddf.) This equivalency establishes the theoretical foundation for the DBM method by allowing it to be viewed as an implementation of the OR model, which has a firm statistical foundation. Since one can obtain the same results using either method, the choice of which procedure to use is mainly dependent on availability of software. Historically the DBM procedure has been more popular, due to the availability of free standalone software and due to its improved performance in its original formulation compared to the original OR formulation. However, an analysis performed by either of the updated DBM or OR methods that incorporates the recent improvements is probably best referred to as an OR-DBM analysis, since the updated approaches give equivalent results. A summary of these developments in the DBM and OR procedures and a discussion of their relationship are provided by Hillis et al. (2008).
16.3.4 Other Study Designs
The OR procedure has been modified to accommodate study designs besides the typical factorial design. These other designs are as follows, with alternative names given in parentheses:
1. Reader-nested-within-test split-plot design (unpaired reader, paired-case design). Cases undergo all tests, but each reader evaluates cases for only one of the tests. This study design is natural when readers are trained to read under only one of the tests.
2. Case-nested-within-test split-plot design (paired reader, unpaired-case design). Each reader evaluates all of the cases, but each case is imaged under only one test, with equal numbers of cases imaged under each test. This design is needed when the diagnostic tests are mutually exclusive, for example, if they are invasive, administer a high radiation dose, or carry a risk of contrast reactions.
3. Case-nested-within-reader split-plot design (paired-case per reader, paired-reader design). Each reader evaluates a different set of cases using all of the diagnostic tests. Compared to a factorial design, the advantage of this design is that typically the same power can be achieved with each reader interpreting fewer cases, but the disadvantage is that the total number of cases is higher.
4. Mixed split-plot design (factorial-nested-within-group design). There are several groups (or blocks) of readers and cases such that each reader and each case belongs to only one group, and within each group all readers evaluate all cases under each test. Each group has the same numbers of readers and cases. The motivation for this study design is to reduce the number of reader interpretations for each reader, compared to the factorial study design, without requiring as many cases to be verified as the case-nested-within reader design.
See Obuchowski (1995) for a discussion of designs 1, 2 and 3, and Obuchowski (2009) and Obuchowski et al. (2012) for a discussion of design 4. Hillis (2014) provides rigorous derivations of the test statistics and their distributions for all of these designs.
16.3.5 My Perspective: OR Versus DBM
In my opinion, it is much more important to become familiar with the OR procedure than the DBM procedure. I say this because the OR procedure, by modeling observed reader performance values rather than pseudovalues, provides a statistical model that has easier-to-interpret parameters and that can more easily be extended to include other study designs. For these reasons, the OR model has seen continued development but there has been no further development of the DBM procedure in the last 10 years. Furthermore, I expect there to be no further development of the DBM procedure in the future, as statisticians much prefer the OR model.
16.3.6 U-Statistic Approach
An alternative method for analyzing MRMC data is the approach proposed by Gallas et al. (Gallas, 2006; Gallas et al., 2009). Although this approach works well and generally produces results very similar to those from the OR-DBM approach, I do not discuss it in this chapter to keep the chapter at a reasonable length and because this approach has the major limitation that the reader performance outcome must be a U-statistic, which excludes many possible outcomes. For example, the nonparametric AUC is a U-statistic, but the semiparametric AUC and the nonparametric and parametric pAUC are not U-statistics. However, this approach does have the advantage of being able to be used with unbalanced designs, although at this writing I and my colleagues are formulating how to use OR-DBM with unbalanced designs. Software for this approach is available from https://github.com/DIDSR/iMRMC/releases (Gallas, 2017).
16.4 Analysis of Van Dyke Data
16.4.1 Software
OR-DBM MRMC 2.51 (Schartz et al., 2018), available for download at http://perception.radiology.uiowa.edu, and LABMRMC, written by Charles Metz and colleagues and available at http://metz-roc.uchicago.edu/MetzROC/software, are to my knowledge, the only free standalone software packages for implementing the DBM/OR procedure. DBM MRMC 2.51 resulted from a collaboration between researchers at the University of Chicago, led by Dr. Charles Metz, and researchers at the University of Iowa, led by Dr. Kevin Berbaum. Compared to LABMRMC, DBM MRMC 2.51 has an improved algorithm and additional features; furthermore, presently LABMRMC is no longer supported.
In this section we use DBM MRMC 2.51 to analyze the data from the example in section 16.2. This software is easy to use and requires no other statistical software. This program offers the user the choice of either a DBM or an OR analysis. I show the OR analysis because, as mentioned above, I believe it is the more important of the two procedures with which to be familiar.
For readers familiar with the statistical software SAS, DBM MRMC 3.x for SAS (Hillis et al., 2007) does the same analyses and is also available for free from the same website as DBM MRMC 2.5. For readers familiar with the FORTRAN programming language, another option for MRMC analysis is the program OBUMRM, written by Dr. Nancy Obuchowski and available at www.lerner.ccf.org/qhs/software/roc_analysis.php.
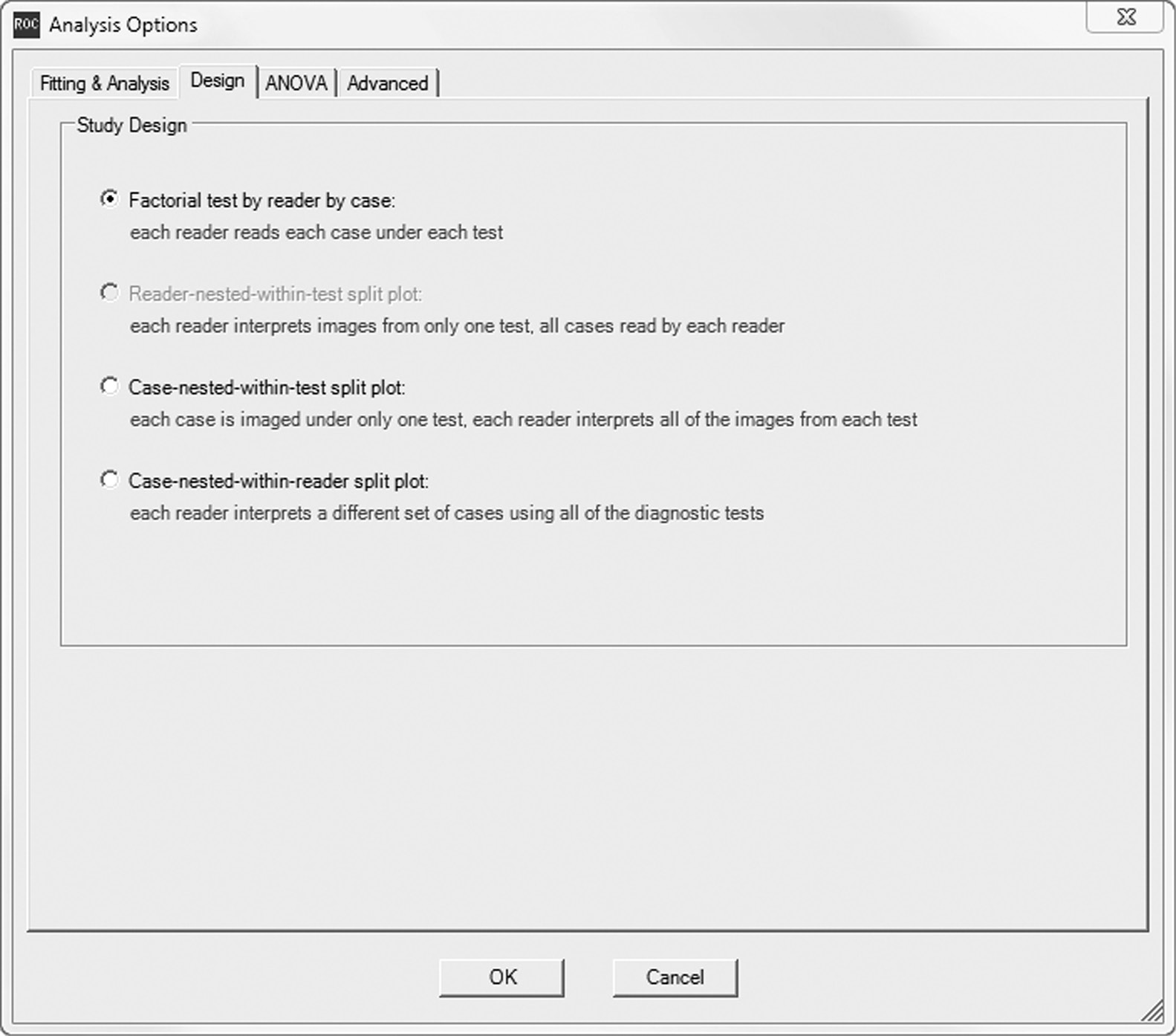
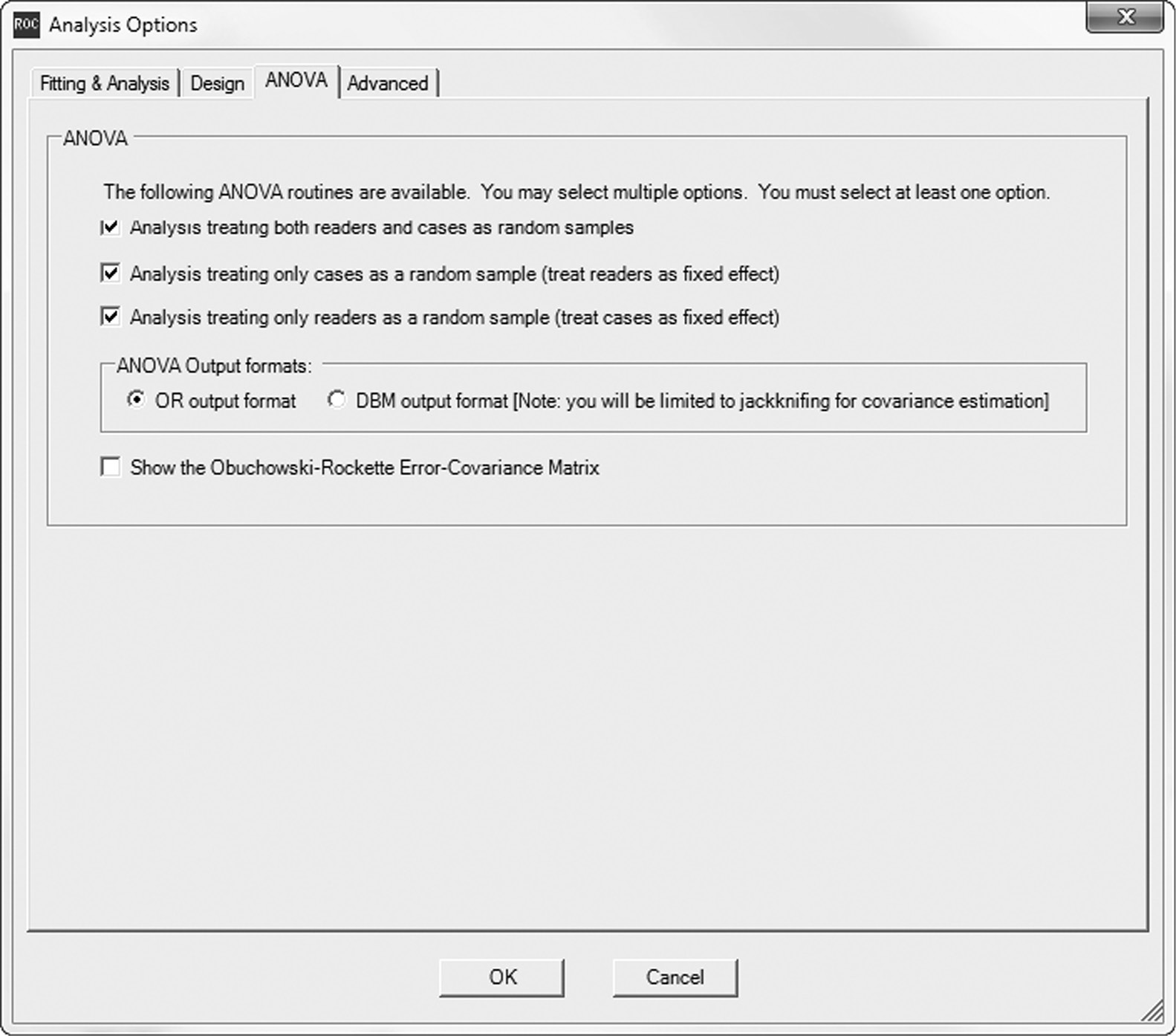
16.4.2 Analysis Options
Figures 16.3–16.7 show submenus of the “Analysis Options” menu (Run ➔ Analysis Options) in DBM MRMC 2.51 which allow the user to specify options for the analysis. In the “Fitting & Analysis” submenu (Figure 16.3) I request trapezoidal/Wilcoxon as the method for estimating the ROC curve and area as the reader performance outcome to be analyzed. In the “Design” submenu (Figure 16.4) I indicate that the data are from a factorial study design; in the “ANOVA” submenu (Figure 16.5) I request all three ANOVA analyses, which I refer to as analysis 1, analysis 2, and analysis 3, and I also request OR output format; and in the “Advanced” submenu (Figure 16.6) I request that the error covariance method be jackknifing. I now discuss each of these options separately.
Figure 16.3 “Fitting & Analysis” options menu for DBM MRMC 2.51 software.
Figure 16.4 “Design” options menu for DBM MRMC 2.5 software.
Figure 16.5 “ANOVA” (analysis of variance) options menu for DBM MRMC 2.5 software.
Figure 16.6 “Advanced” options menu for DBM MRMC 2.5 software.
The trapezoidal/Wilcoxon curve-fitting option provides the nonparametric empirical ROC curve, discussed in section 16.2, which results from connecting the observed (1 – specificity, sensitivity) points with straight lines. In addition to the trapezoidal/Wilcoxon curve-fitting option, there are three other curve-fitting options: PROPROC, contaminated binormal, and RSCORE. The RSCORE option uses the semiparametric method, discussed in Chapter 15, which assumes a latent binormal model. The PROPROC (Metz and Pan, 1999; Pan and Metz, 1997) and contaminated binormal (Dorfman and Berbaum, 2000a, 2000b; Dorfman et al., 2000) methods are alternative semiparametric methods that can be used when a smooth ROC curve is desired. Both the PROPROC and contaminated binormal methods always produce “proper” ROC curves, i.e., curves that never show any “hooks” or crossings of the chance line (i.e., the line defined by sensitivity = 1 – specificity) which sometimes are visible for ROC curves estimated with the RSCORE method, which is not a proper method.
Although the binormal semiparametric method has been used more often than the other two semiparametric methods, many researchers (including myself) prefer the PROPROC method, which will be very similar to the estimated RSCORE curve when the RSCORE curve shows no hooks or chance-line crossings. The contaminated binormal method, which assumes that a fraction of the diseased patients look similar to nondiseased patients, has not been used nearly as much as the RSCORE and PROPROC methods.
The area option specifies that AUC is the reader performance outcome to be analyzed. This outcome, as well as the other outcome options for analysis, is a function of the estimated ROC curve. Other options for outcomes include the partial AUC, sensitivity for a specified specificity, specificity for a specified sensitivity, and expected utility (Abbey et al., 2013, 2014). The AUC, pAUC, and sensitivity for a specified specificity were discussed in section 16.2, as well as in Chapter 15.
Analysis 1 treats both readers and cases as random. This is the OR-DBM analysis. This is the main analysis and is the only one that needs to be performed if the researcher wants to make inferences about both the reader and case populations. Although theoretically analysis 1 can be performed with as few as two or three readers, results are more convincing with at least four or five readers, since then the sample seems more likely to be representative of a population of similar readers. Furthermore, more readers result in more power. Thus I recommend that a study have at least four, preferably five, readers, if the goal is to generalize to both reader and case populations.
Analysis 2 treats cases as random but readers as fixed. Thus conclusions apply to the population of cases but only for the readers in the study. Although this analysis is performed within the OR framework, this should technically not be referred to as an OR analysis. This analysis treats both treatment and reader as fixed; see Hillis et al. (2005, p. 1593) for a discussion of this analysis.
If financial or logistical concerns limit the number of readers to fewer than four, then I recommend using analysis 2. Even though such a study does not generalize to readers, it can provide an important first step in establishing a conclusion (e.g., one modality is superior when used by the readers in the study) when previous studies have not been undertaken.
Typically, but not always, analysis 2 will give more significant results than analysis 1 because it only makes inferences about one population instead of two. Thus if analysis 1 does not yield a significant finding but analysis 2 does, the analysis 2 finding would be of interest to also report since it suggests that the analysis 1 insignificant finding may be due to insufficient sample size.
Analysis 3 treats readers as random but cases as fixed. This analysis is appropriate when the only cases of interest are the study cases; for example, when “cases” consist of prespecified locations of one phantom and of interest is the comparison of modalities for this particular phantom. The comments about analysis 2 also apply to analysis 3: this is technically not OR, and a nonsignificant analysis 1 coupled with a significant analysis 3 suggests insufficient sample size for analysis 1. This analysis is equivalent to a conventional repeated-measures treatment-by-reader ANOVA of the accuracy estimates, with reader treated as a random factor and modality treated as a fixed repeated-measures factor. For two treatments this analysis is the same as a paired t-test, which is equivalent to a one-sample t-test applied to the modality differences, one for each reader.
Related posts:
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
