8 Thoracic Aorta and Major Branches
Anatomy
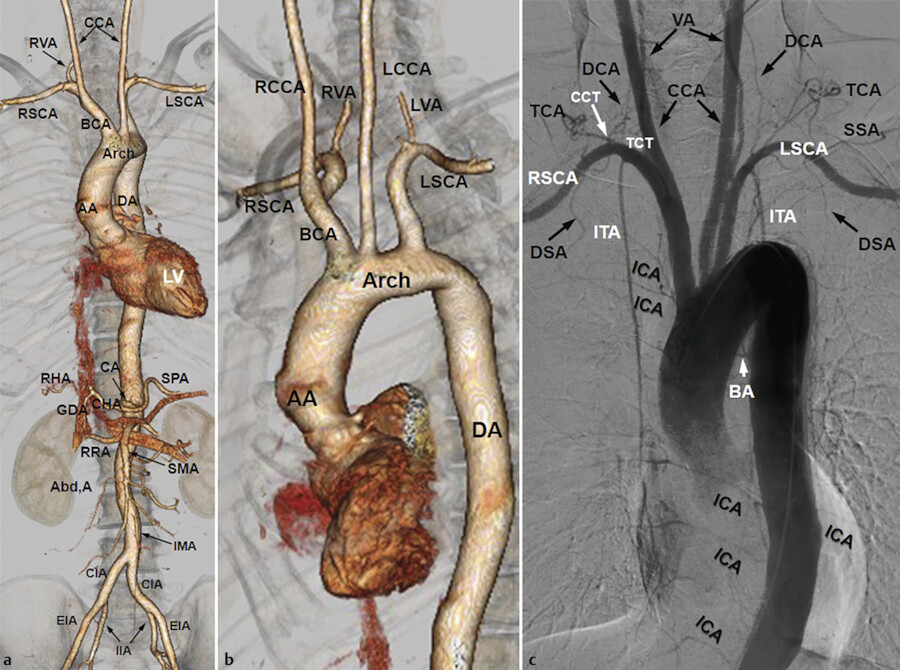
The aorta is the largest artery originating at the upper part of the left ventricle. It can be divided into four sections: the ascending aorta, the aortic arch, the thoracic (descending) aorta, and the abdominal aorta (Fig. 8‑1). The aorta ascends obliquely to the right within the pericardium, between the superior vena cava and main pulmonary artery, and anterior to the right pulmonary artery and trachea (ascending aorta). At T3 to T4 level, it turns backward to form the aortic arch. It descends within the thorax on the left side of the vertebral column (descending aorta) into the abdomen through the aortic hiatus in the diaphragm (abdominal aorta).
Ascending Aorta
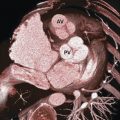
The origin of the ascending aorta (the aortic root) shows anatomical dilation just above each of the aortic valve leaflets known as the sinuses of Valsalva. These three aortic sinuses include the left coronary, the right coronary, and the noncoronary (nonadjacent) sinuses. 1 The left aortic sinus and right aortic sinus, give rise to the left and right coronary arteries (RCAs), respectively (Fig. 8‑2). The transverse diameter of the aorta at the level of the sinus is usually less than 3.5 cm. A diameter above 4 cm is abnormal. Sinuses of Valsalva are equal in size but rarely one or all can become aneurysmal. 2 Aneurysm of the sinus of Valsalva can be congenital or acquired, more common in men, and rarely can rupture. The ascending aorta is about 33 mm in diameter and 5 cm in length in adult human. The upper limit of normal diameter of the ascending aorta is about 41 mm. 3



Branches from the Ascending Aorta
Right Coronary Artery
Detail of the anatomy of the coronary arteries is described in Chapter 18. The RCA runs between the right ventricular outflow tract and the right atrial appendage and descends through the right atrioventricular groove (Fig. 8‑2). It curves posteriorly toward the crux of the heart and continues downward in the posterior interventricular sulcus. 4 The RCA gives off branches to the right ventricular outflow tract (conus branch), sinoatrial node (sinoatrial nodal artery), the right atrium, and the right ventricle (the right marginal branch is the largest one). It also gives branches to the inferior wall of the left ventricle which adjoins the posterior interventricular sulcus.
Left Coronary Artery
The left coronary artery passes between the pulmonary trunk and the left atrial appendage, and it divides into the left anterior descending artery (LAD) and the left circumflex artery (LCx) (Fig. 8‑1 , Fig. 8‑3). The LAD runs downward along the anterior interventricular groove, which gives branches to the ventricles and interventricular septum. The largest branch of the LAD is the diagonal branch supplying blood to the anterolateral portion of the left ventricle. The LCx travels in the left atrioventricular groove to reach the back of the heart. It gives off branches to supply the left atrium and the posterior and lateral free walls of the left ventricle.



Coronary artery anomalies such as anomalous in origin, course, and number are relatively common with higher frequency in congenital cardiac diseases. 5 , 6 Coronary artery fistulas, including coronary–pulmonary arterial fistulas, coronary–bronchial arterial anastomoses, coronary artery–cardiac chamber fistulas, and coronary artery–systemic venous fistulas, are found in 0.9 % of patients undergone coronary computed tomography (CT) angiography. 7 Majority of coronary artery anomalies are asymptomatic, but they can cause angina, ischemic heart attack, sudden death, heart failure, pulmonary hypertension, and pulmonary hemorrhage.
Aortic Arch
The aortic arch begins at the level of the second sternocostal joint. It runs upward and bends posteriorly to the left, and then descends to connect to the descending aorta at the level of the T4 vertebra. Three major branches originating from aortic arch include the brachiocephalic artery, the left common carotid artery, and the left subclavian artery (Fig. 8‑1 , Fig. 8‑3). The aortopulmonary ligament (ligamentum arteriosus), an embryological remnant of the ductus arteriosus, connects the distal portion of the aortic arch with the pulmonary trunk. Blunt aortic injuries often result in disruption of the aorta near the aortopulmonary ligament. 8 The left recurrent laryngeal nerve, a branch of the vagus nerve, hooks around the aortic arch to the left of the aortopulmonary ligamentum and ascends between the trachea and esophagus. 9 The right recurrent laryngeal nerve hooks around the right subclavian artery and ascends into the neck.
Branches from the Aortic Arch
Brachiocephalic Artery
The brachiocephalic artery (the innominate artery) is the first and the largest branch arising from the aortic arch. It runs obliquely upward to the right to the level of the right sternoclavicular joint where it divides into the right common carotid artery and the right subclavian artery. The length of the brachiocephalic artery varies and can elongate with age and arteriosclerosis causing widening of the superior mediastinum on plain radiographs. The brachiocephalic artery occasionally gives off the thyroid ima artery, a branch supplying the inferior part of the thyroid gland (Fig. 8‑3). 10 , 11
A tracheal artery and/or bronchial artery may also arise from the brachiocephalic artery either as a single branch or a common trunk with the thyroid ima artery. 12
Right Common Carotid Artery
The right common carotid artery, originating from the brachiocephalic artery, runs upward in the deep cervical space and divides into the external and internal carotid arteries at the level of the upper border of the thyroid cartilage (Fig. 8‑3). It is contained in the carotid sheath together with the internal jugular vein and the vagus nerve. The common carotid artery lies medial to the internal jugular vein, and the vagus nerve runs posteriorly between the two vessels. The superior thyroidal artery occasionally arises from the distal portion of the common carotid artery.
Right Subclavian Artery
The right subclavian artery, originating from the brachiocephalic artery, runs superolaterally, passing between anterior and middle scalene muscles, and then runs inferolaterally (Fig. 8‑3 , Fig. 8‑4). The subclavian artery becomes the axillary artery at the outer margin of the first rib. The brachial plexus also passes between anterior and middle scalene muscles and runs along the subclavian artery. Thoracic outlet syndrome can occur by compression of the subclavian artery and/or the brachial plexus between the anterior and middle scalene muscles and/or between the first rib and clavicle causing pain, weakness of the hand and arm, and discoloration of the hand. 13

Left Common Carotid Artery and the Left Subclavian Artery
The left common carotid artery and the left subclavian artery are the second and the third branches originating from aortic arch, respectively. Both run superolaterally from the superior mediastinum to the neck, and then run on a path similar to the contralateral side. The left common carotid artery can originate from the brachiocephalic artery in 10% of cases. This branching type is called “bovine arch” (Fig. 8‑5). 14

Branches of the Subclavian Arteries
The subclavian arteries give off various branches supplying the neck, shoulder, chest wall, and brain.
The Vertebral Artery
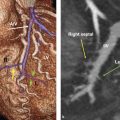
The vertebral artery is the first branch arising from the upper part of the proximal portion of the subclavian artery, which ascends through the transverse foramen of the sixth cervical vertebra (Fig. 8‑6 , Fig. 8‑7). It runs upward into the posterior fossa through the foramen magnum and joins the contralateral vertebral artery to form the basilar artery. The cervical portion of the vertebral artery gives off branches to the adjacent muscles (muscular branches), vertebrae (vertebral branches), spinal cord (anterior and posterior spinal arteries), and cervical nerves (radicular arteries) (Fig. 8‑7). 15 The posterior meningeal artery supplying the dura matter of the posterior fossa, and the posterior inferior cerebellar artery supplying the medulla and cerebellum arise from distal portion of the vertebral artery around the craniocervical junction.


The Internal Thoracic Artery
The internal thoracic artery (internal mammary artery) originates from the proximal portion of the subclavian artery across the origin of the thyrocervical trunk (Fig. 8‑3). It passes behind the subclavian vein and the first rib and descends in the anterior chest wall along the lateral margin of the sternum. It supplies the anterior chest wall, mediastinum, sternum, and thymus, before terminating into the musculophrenic and superior epigastric arteries (Fig. 8‑8). 16 It may arise from a common trunk with the suprascapular or inferior thyroid arteries.

The Thyrocervical Trunk
The thyrocervical trunk, the second ascending branch of the subclavian artery, originates at the inner border of the anterior scalene muscle. The thyrocervical trunk is the short common trunk for four important arterial branches including the inferior thyroid artery, the ascending cervical artery, the suprascapular artery, and the transverse cervical artery (Fig. 8‑3 , Fig. 8‑9). The inferior thyroid artery runs superomedially and gives off branches to the inferior part of the thyroid gland, larynx, trachea, and the esophagus. The ascending cervical artery ascends behind the carotid sheath to the transverse process of the cervical vertebra. The ascending cervical artery gives off small muscular and vertebral branches and provides anastomotic arteries with branches of the vertebral artery. It may give off a branch to the spinal cord, an anterior or posterior spinal artery. The suprascapular artery and the transverse cervical artery run laterally and supply the surrounding muscles and bony structures. These arteries occasionally arise independently from the subclavian artery at its distal portion. The dorsal scapular artery can arise from the transverse cervical artery in approximately 30% of cases. 17

The Costocervical Trunk
The costocervical trunk arises from posterosuperior aspect of the subclavian artery. It divides into the deep cervical artery and the highest (superior) intercostal artery (Fig. 8‑1 , Fig. 8‑10). The deep cervical artery runs posteriorly between the first rib and transverse process of the seventh cervical vertebra, and then ascends deeply in the posterior cervical space (Fig. 8‑3 , Fig. 8‑10). It supplies the posterior cervical muscles and anastomoses with the muscular branches of the vertebral and occipital arteries (Fig. 8‑7). It may give off an anterior or posterior spinal artery between the seventh cervical and first thoracic vertebrae (Fig. 8‑11). The deep cervical artery is occasionally absent, which can be replaced by other branches such as the superficial branches of the transverse cervical artery. The highest intercostal artery descends in front of the first and second ribs and often anastomoses with an intercostal artery from descending aorta (Fig. 8‑10). It supplies adjacent muscles, bony structures, and gives off small spinal branches.


The Dorsal Scapular Artery
The dorsal scapular artery arises from the distal portion of the subclavian artery in more than 60% of cases. It runs posteriorly to supply the levator scapulae muscle and the rhomboid muscle (Fig. 8‑1 , Fig. 8‑8). The dorsal scapular artery may originate from the transverse cervical artery in 30% of cases (Fig. 8‑4). 17 It then descends to supply the medial part of the scapula and anastomoses with the intercostal arteries and branches of the subscapular artery from the axillar artery.
Descending Thoracic Aorta
The descending thoracic aorta is continuous with the aortic arch at the level of the fourth thoracic vertebra. It descends in the posterior mediastinum to reach the aortic hiatus of the diaphragm at the lower border of the 12th thoracic vertebra where it becomes the abdominal aorta. The descending aorta lies on the left of the vertebral column at its beginning, and it descends medially. It lies in front of the vertebral column at its termination. It gives off segmental intercostal arteries, and arteries to the bronchi and esophagus (Fig. 8‑1).
Branches from Descending Aorta
Intercostal and Subcostal Arteries
The nine paired segmental arteries from the 3rd to 11th intercostal artery originate from the descending aorta, which supply the intercostal spaces, vertebral body, paravertebral muscle, nerve roots, and spinal cord (Fig. 8‑12). The subcostal arteries below the 12th ribs supply the flat abdominal wall muscles. There are longitudinal paravertebral and epidural anastomoses between the intercostal arteries at consecutive levels. There are also transverse anastomoses between the paraspinal and epidural arteries on each side communicating the intercostal arteries with the contralateral ones (Fig. 8‑13). 14
The intercostal artery divides into two branches named intercostal/lateral muscular branch and the dorsal spinal branch. The dorsal spinal branch further divides into the dorsal, epidural, meningeal, and radiculomeningeal branches, and sometimes radiculopial (posterior spinal) or radiculomedullary (anterior spinal) arteries (Fig. 8‑12). The artery of Adamkiewicz is the name given to the largest radiculomedullary artery that supplies the spinal cord. 14 , 18 It ascends medially to the anterior surface of the spinal cord along with the nerve root, and then continues along the anterior spinal artery forming a typical “hairpin turn” at the midline (Fig. 8‑14). The artery of Adamkiewicz originates between T8 and L1 in 92% of cases. It is seen predominantly on the left side (70%). 19



Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree