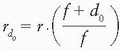A System of Dosimetric Calculations
Several methods are available for calculating absorbed dose in a patient. Two of these methods using percent depth doses (PDDs) and tissue-air ratios (TARs) were discussed in Chapter 9. However, there are some limitations to these methods. For example, the dependence of PDD on source to surface distance (SSD) makes this quantity unsuitable for isocentric techniques. Although TARs and scatter-air ratios (SARs) eliminate that problem, their application to beams of energy higher than those of 60Co has been seriously questioned (1, 2, 3) as they require measurement of dose in free space. As the beam energy increases, the size of the chamber buildup cap for in-air measurements has to be increased and it becomes increasingly difficult to calculate the dose in free space from such measurements. In addition, the material of the buildup cap is usually different from that of the phantom and this introduces a bias or uncertainty in the TAR measurements.
In order to overcome the limitations of the TAR, Karzmark et al. (1) introduced the concept of tissue-phantom ratio (TPR). This quantity retains the properties of the TAR but limits the measurements to the phantom rather than in air. A few years later, Holt et al. (4) introduced yet another quantity, tissue-maximum ratio (TMR), which also limits the measurements to the phantom.
In this chapter, we describe a dosimetric system based on the TPR and TMR concepts. This system was originally developed by Khan et al. (5) for the calculation of dose and monitor units for any energy beam, field size, and depth.
10.1. DOSE CALCULATION PARAMETERS
The dose to a point in a medium may be analyzed into primary and scattered components. The primary dose is contributed by the primary or original photons emitted from the source and the scattered dose is the result of the scattered photons. The scattered dose can be further separated into collimator and phantom components, because the two can be varied independently (e.g., by blocking). For example, blocking a portion of the field does not significantly change the incident output or photon energy fluence in the open portion of the beam (6,7) but may significantly reduce the phantom scatter depending upon the extent of blocking.
The above analysis presents one practical difficulty, namely the determination of primary dose in a phantom that excludes both the collimator and phantom scatter. However, for megavoltage photon beams, one may, as a reasonable approximation, consider collimator scatter as part of the primary beam so that the phantom scatter could be calculated separately. Therefore, we define an effective primary dose as the dose due to the primary photons as well as those scattered from the collimating system. The effective primary in a phantom may be thought of as the dose at depth minus the phantom scatter. Alternatively, the effective primary dose may be defined as the dose expected in the field when scattering volume is reduced to zero while keeping the collimator opening constant.
Representation of primary dose in a phantom by the dose in a 0 × 0 field poses practical problems because of the lack of lateral electronic equilibrium. Consequently, this makes direct measurement of the primary dose impossible. This issue has been discussed and debated in the literature (8,9), but practical solutions are still not agreed on. Systems that use electron transport in the calculation of primary and scattered components of dose would be appropriate but are not as yet fully developed and implemented for routine calculations. Until then, the concept of a 0 × 0 field to represent the primary dose with the implicit assumption that lateral electronic equilibrium exists at all points will continue to be used for routine dosimetry.
Notwithstanding the weakness of the above assumption, primary dose in a phantom is usually represented by the dose in a hypothetical 0 × 0 field which is obtained by extrapolation of the depth dose versus field size data. In practice, this extrapolation is made down to a field size just large enough to provide lateral electronic equilibrium (e.g., 3 × 3 or 4 × 4 cm2 for most energies). The extrapolated curve is then extended to 0 × 0 field size.
A. COLLIMATOR SCATTER FACTOR (IN-AIR OUTPUT RATIO)
The beam output (exposure rate, dose rate in free space, or energy fluence rate) measured in air depends on the field size. As the field size is increased, the output increases because of the increased collimator scatter,1 which is added to the primary beam.
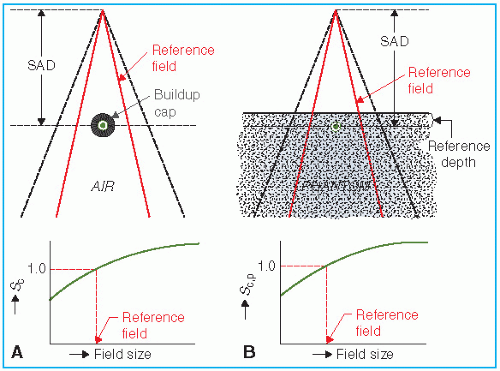
The collimator scatter factor (Sc) is also called the in-air output ratio (10) and may be defined as the ratio of the output in air for a given field to that for a reference field (e.g., 10 × 10 cm2). Sc may be measured with an ion chamber with a buildup cap of a size large enough to provide maximum dose buildup for the given energy beam. The measurement setup is shown in Figure 10.1A. Ionization readings are plotted against field size [side of equivalent square or area/perimeter (A/P)] and the values are normalized to the reference field (e.g., 10 × 10 cm2).
In the measurement of Sc, the field must fully cover the buildup cap (without penumbral effects) for all field sizes if measurements are to reflect relative photon energy fluences. A lateral margin of at least 1 cm between the field edge and the buildup cap is considered adequate.
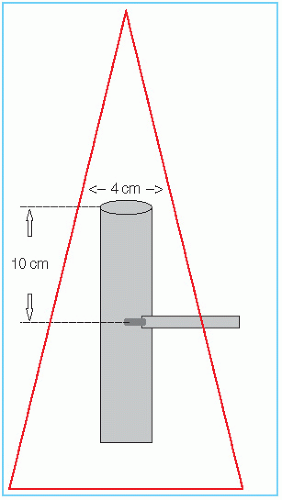
For high-energy photon beams, the required buildup cap size can become too large to be able to measure Sc for small field sizes. For these cases, van Gasteren et al. (11) proposed the use of a narrow (e.g., 4 cm diameter) cylindrical beam-coaxial phantom or “miniphantom,” with a measurement depth sufficiently beyond dmax to avoid contaminant electrons (e.g., 10 cm). A diagram of a miniphantom is displayed in Figure 10.2. The use of miniphantoms for Sc measurements is recommended by the AAPM TG-74 report (10).
Normally, the collimator scatter factors are measured with the chamber at the source to axis distance (SAD). However, for small fields, one may take the output measurements (including those for the reference field) at distances larger than the SAD so that the smallest field covers the buildup cap or miniphantom with a suitable margin. The field sizes in these measurements are all defined at the SAD.
B. PHANTOM SCATTER FACTOR
The phantom scatter factor (Sp) takes into account the change in scatter radiation originating in the phantom at a reference depth as the field size is changed. Sp may be defined as the ratio of the dose rate (or dose per monitor unit (MU)) for a given field at a reference depth to the dose rate
at the same point and depth for the reference field (e.g., 10 × 10 cm2), with the same collimator opening (i.e., same incident energy fluence). In this definition, it should be noted that Sp is related to the changes in the volume of the phantom irradiated for a fixed collimator opening. Thus, one could determine Sp by using a large field incident on phantoms of different cross-sectional sizes.
at the same point and depth for the reference field (e.g., 10 × 10 cm2), with the same collimator opening (i.e., same incident energy fluence). In this definition, it should be noted that Sp is related to the changes in the volume of the phantom irradiated for a fixed collimator opening. Thus, one could determine Sp by using a large field incident on phantoms of different cross-sectional sizes.
For photon beams for which backscatter factors can be accurately measured (e.g., up to cobalt-60), Sp factor at the reference depth of maximum dose may be defined simply as the ratio of backscatter factor (BSF) [also called peak scatter factor (PSF)] for the given field to that for the reference field (see Appendix, Section A). Mathematically, for such beams:

where r is the side of the equivalent square field and r0 is the side of the reference field (e.g., 10 × 10 cm2).
A more practical method of measuring Sp, which can be used for all beam energies, consists of indirect determination from the following equation (for derivation, see Appendix, Section A):

where Sc,p(r) is the total scatter factor defined as the dose rate (or dose per MU) at a reference depth for a given field size r divided by the dose rate at the same point and depth for the reference field (e.g., 10 × 10 cm2) (Fig. 10.1B). Thus, Sc,p(r) contains both the collimator and phantom scatter and when divided by Sc(r) yields Sp(r).
C. TISSUE-PHANTOM AND TISSUE-MAXIMUM RATIOS
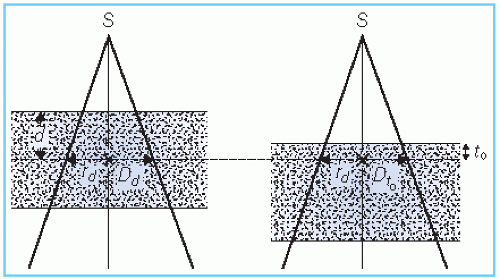
TPR is defined as the ratio of the dose rate at a given depth in phantom to the dose rate at the same source-point distance, but at a reference depth. This is illustrated in Figure 10.3. The corresponding quantity for the scattered dose calculation is called the scatter-phantom ratio (SPR), which is analogous in use to the SAR discussed in the previous chapter. Details of the TPR and SPR concepts and their properties have been discussed in the literature (1,3,5).
TPR is a general function that may be normalized to any reference depth (e.g., reference depth of maximum dose or 10 cm depth). Although there is no general agreement concerning the reference depth to be used for this quantity, the point of central axis dmax has a simplicity that is very desirable in dose computations. If dmax is adopted as a fixed reference depth, the quantity TPR gives rise to the TMR. Thus, TMR is thus a special case of TPR and may be defined as the ratio of the dose rate at a given point in phantom to the dose rate at the same source-point distance and at the reference depth of maximum dose (Fig. 10.3).
For megavoltage photon beams, the depth of maximum dose has been found to depend on field size (12,13) as well as on SSD (14,15). This dependence arises due to the change in electron contamination at the surface as a function of field size and SSD. For the calculative functions to be independent of incident electron contamination, they should not be normalized to dose in the buildup region. In other words, the reference depth of normalization must be greater than the range of contaminant electrons.
Since electron contamination increases with field size and decreases with SSD, the depth of maximum dose (dm) tends to decrease with field size (12) and increase with SSD (14,15). Therefore, if dm is chosen to be the reference depth for all field sizes and SSDs, it should be that for the smallest field required for lateral electronic equilibrium (e.g., 3 × 3 cm2) and a large SSD (100cm or larger). Under these conditions, the electron contamination is minimal and the dose at dm approaches that for a pure photon beam. Alternatively, one may plot [(%DD) × (SSD + d)2] as a function of depth d to find dm (15). This eliminates dependence on SSD. The reference dm can then be obtained by plotting dm as a function of field size (down to 3 × 3 cm2) and extrapolating to 0 × 0 field size.
The reference depth of maximum dose (t0) as determined above should be kept the same for all field sizes and all the relevant dosimetric quantities (e.g., PDDs, TMRs, Sp factors, and the depth at which the dose per MU is set for accelerator calibration) should be normalized to this depth.
For the TPRs, we denote the reference depth by d0. If d0 is chosen to be 10 cm, the formalism for dose calculations based on TPRs must also ensure that all the relevant dosimetric quantities, (e.g., TPRs, PDDs, Sp factors, and the calibration dose/MU) are normalized to the same reference depth.
C.1. Relationship between Tissue-Maximum Ratio and Percent Depth Dose
For TMRs, it is assumed that the fractional scatter contribution to the depth dose at a point is independent of the divergence of the beam and depends only on the field size at the point and the depth of the overlying tissue. This has been shown to be essentially true by Johns et al. (16). This principle, which also underlies TAR and TPR, makes all these functions practically independent of SSD. Thus, a single table of TMRs can be used for all SSDs for each radiation quality.
Figure 10.4 shows TMR data for 10-MV x-ray beams as an example. The curve for 0 × 0 field size shows the steepest drop with depth and is caused entirely by the primary beam. For megavoltage beams, the primary beam attenuation can be approximately represented by
where µ is the effective linear attenuation coefficient and t0 is the reference depth of maximum dose. µ can be determined from TMR data by plotting µ as a function of field size (side of equivalent square) and extrapolating it back to 0 × 0 field.
TMR and percent depth dose P are interrelated by the following equation (see Appendix, Section B, for derivation):
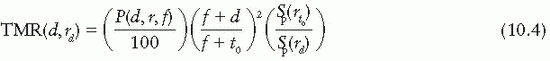
where
P is the percent depth dose, d is the depth, t0 is the reference depth of maximum dose, r is the field size at the surface, 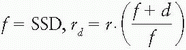 , and
, and 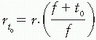 . In Equation (10.4), the percent depth dose P is normalized to the dose at the reference depth t0 so that P(t0, r, f) = 100 for all field sizes and SSDs.
. In Equation (10.4), the percent depth dose P is normalized to the dose at the reference depth t0 so that P(t0, r, f) = 100 for all field sizes and SSDs.
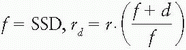 , and
, and 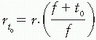 . In Equation (10.4), the percent depth dose P is normalized to the dose at the reference depth t0 so that P(t0, r, f) = 100 for all field sizes and SSDs.
. In Equation (10.4), the percent depth dose P is normalized to the dose at the reference depth t0 so that P(t0, r, f) = 100 for all field sizes and SSDs.Although TMRs can be measured directly, they can also be calculated from percent depth doses, as shown by Equation 10.4. For 60Co, Equations 10.2 and 10.4 can be used to calculate
TMRs. In addition, TMRs can be derived from TAR data in those cases, such as 60Co, where TARs are accurately known:
TMRs. In addition, TMRs can be derived from TAR data in those cases, such as 60Co, where TARs are accurately known:
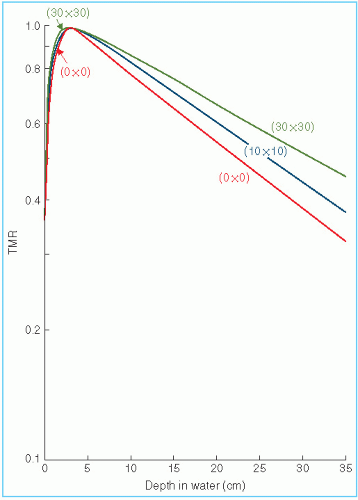 Figure 10.4. Plot of tissue-maximum ratio (TMR) for 10-MV x-rays as a function of depth for a selection of field sizes. |
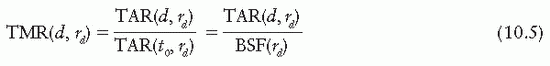
C.2. Relationship between Tissue-Phantom Ratio and Percent Depth Dose
Equation 10.4 for TMR may be generalized to TPR for any reference depth (e.g., 10 cm):
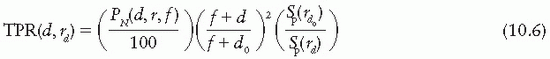
The normalized percent depth doses can be obtained from the regular percent depth doses (P) (which are normalized to a reference depth of maximum dose, t0) by using the following equation:
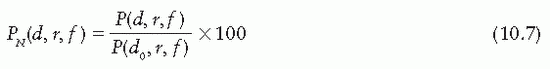
D. SCATTER-PHANTOM AND SCATTER-MAXIMUM RATIOS
SPR and SMR, like the SAR, are quantities designed specifically for the calculation of scattered dose in a medium. Mathematically,
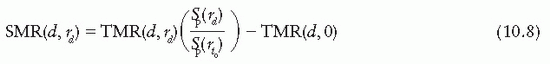
and
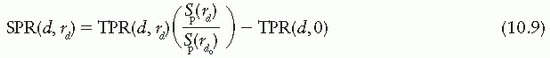
For derivation of the above equations, see Appendix, Section C.
From Equations 10.1, 10.5, and 10.8, it can be shown that for 60Co γ rays, SMRs are approximately the same as SARs. However, for higher energies, SMRs should be calculated from TMRs by using Equation 10.8.
Another interesting relationship can be obtained at the reference depth of maximum dose (t0). Since TMR at depth t0 is unity by definition, Equation 10.8 for this depth reduces to

Similarly, since TPR at depth d0 is unity, Equation 10.9 for this depth reduces to
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree