and Ashutosh Dash2
(1)
Nuclear Security and Isotope Division, Oak Ridge National Laboratory, OAK RIDGE, USA
(2)
Isotope Production and Applications Division, Bhabha Atomic Research Centre, Mumbai, India
6.1 Introduction
Cyclotrons are generally used for the preparation of neutron-deficient radionuclides, which decay mostly by 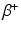 emission or electron capture (EC), which are used for diagnostic applications (IAEA 2009). However, these production facilities are also sometimes used for the production of therapeutic
emission or electron capture (EC), which are used for diagnostic applications (IAEA 2009). However, these production facilities are also sometimes used for the production of therapeutic 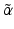 emitting and
emitting and 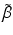 —emitting radionuclides. In some instances, Auger- and Conversion electron-emitting (CE) therapeutic radioisotopes are also reactor-produced, but in general, the large majority of radioisotopes used for therapy are reactor-produced. Because of the power requirements, operational costs, and in general focused operations, cyclotron production of radionuclides is generally more expensive compared with those produced by reactor irradiation. With reactors, the general operation is not affected by target insertion and radiation, and usually many different experiments and irradiations are concurrently conducted. However, higher specific activities (SA) are generally available from the accelerator production routes, and no-carrier-added products (NCA) can often be obtained because the atomic number, Z, usually changes (Fig. 6.1).
—emitting radionuclides. In some instances, Auger- and Conversion electron-emitting (CE) therapeutic radioisotopes are also reactor-produced, but in general, the large majority of radioisotopes used for therapy are reactor-produced. Because of the power requirements, operational costs, and in general focused operations, cyclotron production of radionuclides is generally more expensive compared with those produced by reactor irradiation. With reactors, the general operation is not affected by target insertion and radiation, and usually many different experiments and irradiations are concurrently conducted. However, higher specific activities (SA) are generally available from the accelerator production routes, and no-carrier-added products (NCA) can often be obtained because the atomic number, Z, usually changes (Fig. 6.1).
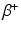 emission or electron capture (EC), which are used for diagnostic applications (IAEA 2009). However, these production facilities are also sometimes used for the production of therapeutic
emission or electron capture (EC), which are used for diagnostic applications (IAEA 2009). However, these production facilities are also sometimes used for the production of therapeutic 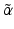 emitting and
emitting and 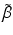 —emitting radionuclides. In some instances, Auger- and Conversion electron-emitting (CE) therapeutic radioisotopes are also reactor-produced, but in general, the large majority of radioisotopes used for therapy are reactor-produced. Because of the power requirements, operational costs, and in general focused operations, cyclotron production of radionuclides is generally more expensive compared with those produced by reactor irradiation. With reactors, the general operation is not affected by target insertion and radiation, and usually many different experiments and irradiations are concurrently conducted. However, higher specific activities (SA) are generally available from the accelerator production routes, and no-carrier-added products (NCA) can often be obtained because the atomic number, Z, usually changes (Fig. 6.1).
—emitting radionuclides. In some instances, Auger- and Conversion electron-emitting (CE) therapeutic radioisotopes are also reactor-produced, but in general, the large majority of radioisotopes used for therapy are reactor-produced. Because of the power requirements, operational costs, and in general focused operations, cyclotron production of radionuclides is generally more expensive compared with those produced by reactor irradiation. With reactors, the general operation is not affected by target insertion and radiation, and usually many different experiments and irradiations are concurrently conducted. However, higher specific activities (SA) are generally available from the accelerator production routes, and no-carrier-added products (NCA) can often be obtained because the atomic number, Z, usually changes (Fig. 6.1).
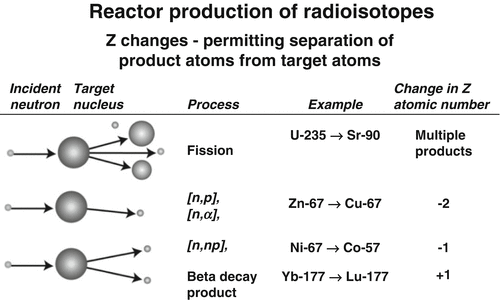
Fig. 6.1
Examples of particle reactions where Z changes and radioisotopic products can be separated from target atoms by traditional methods
As summarized in Table 6.1, a variety of accelerator-produced radioisotopes are of current interest for targeted therapy.
Table 6.1
Key examples of accelerator-produced therapeutic radionuclides
Product Nuclide | Principle emission Type | Half-Life | Key examples Production route |
|---|---|---|---|
Actinium-225 | Alpha | 10 days | Thorium |
Astatine-211 | Alpha | 7.21 h | |
Copper-67 | Beta | 2.58 days | natZn/68Zn(p,2p)67Cu 70Zn(p,α)67Cu |
Gallium-67 | Auger | 3.26 days | 68Zn(p,2n)67Cu 64Zn(d,2n)67Cu 65Cu(α,2n)67Cu |
Indium-111 | Auger | 2.8 days | 111Cd(p,n)111In 112Cd(p,2n)111In |
Radium-223 | Alpha | 11.4 days | Thorium |
Rhenium-186 | Beta | 3.78 days | 186W(p,n)186Re 186W(d,2n)186Re |
Tin-117 m | CE | 13.6 days | natSb(p,xn)117mSn |
6.2 Accelerators for Radionuclide Production
The use of accelerators for production of medical radionuclides requires the delivery of charged particle beams which have two primary characteristics, since they must both have sufficient energy to induce the desired nuclear reaction and sufficient beam current to provide practical product yields. The basic characteristics of a medical cyclotron, for instance, include an ion source for ion production, an acceleration chamber for ion acceleration, a magnet to contain the ions on a circular path, and finally a stripper to “extract” the ions from the accelerator and direct on the target (Fig. 6.2). The extracted beam can be appropriately tuned to focus on a target or a few targets in separated beam stops simultaneously, since the beam can be focused within the accelerator itself or can be focused on a target station which is located exterior to the accelerator. The targets can consist of a solid, liquid, or gas (IAEA 2009).


Fig. 6.2
Medical cyclotron, (a) internal view. (b) Medical cyclotron at RMC, India
When an energetic-charged particle passes through any material, there is a definite probability to interact with nucleus of atoms along its path. The particle may be scattered off the nucleus or, if the energy is high enough when collision occurs, may combine to form a compound nucleus which will then decompose through one of the several possible pathways, leading to the formation of the product radionuclide. Another important and often challenging requirement is the availability of efficient chemical methods for separation of the microscopic levels of the radionuclide products from the macroscopic target levels, which in turn must often be recovered for recycling for subsequent irradiation.
6.2.1 Calculation of Production Yield
The rate of radionuclide production is dependent on a number of factors, including the magnitude of the reaction cross section (i.e., probability of capture) as a function of energy; the incident particle energy; the thickness of the target in atoms per cm2, which will determine the exit particle energy; and the flux of incoming particles. In the simplest case, where the cross section is assumed to be constant, the rate of production is given by the equation:
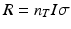
where:
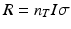
(6.1)
R is the number of nuclei formed per second.
n T is the target thickness in nuclei/cm2.
I is the incident particle flux per second and is related to the beam current.
σ is the reaction cross section, or probability of interaction, expressed in cm2 and is a function of energy.
The cross section is always a function of energy, and hence Eq. (6.1) becomes modified as:
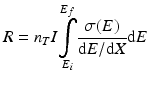
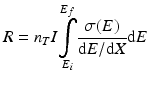
(6.2)
E is the energy of the incident particles.
x is the distance travelled by the particle.
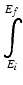 is the integral from the initial energy to the final energy of the incident particle along its path.
is the integral from the initial energy to the final energy of the incident particle along its path.
As the charged particles passes through the target material, energy is lost due to interactions with the target electrons which is represented in the above equation by the term dE/dx (also called the “stopping power”).Returning to the expression for the cross section, it is evident that n T is given by the following expression:
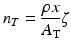
where:
If the target material is a compound rather than a pure element, then the number of nuclei per unit area is given by the following expression:
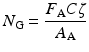
where:
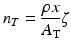
(6.3)
n T is the target thickness in nuclei/cm2.
ρ is the density in g/cm3.
x is the distance the particle travels through the material.
ζ is Avogadro’s number.
A T is the atomic weight of the target material in grams.
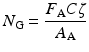
(6.4)
N G is the number of target nuclei per gram.
F A is the fractional isotopic abundance.
C is the concentration by weight.
A A is the atomic mass number of nucleus A.
The above equations illustrate that it is not always possible to eliminate the radionuclidic impurities in the product during radionuclide production using cyclotrons. This occurs even when using the highest isotopic target enrichment and the most precise energy selection, resulting from incident particle energy depletion with initiation of secondary nuclear reactions which is increased with higher-energy incident particles.
6.2.2 Saturation Factor
Radionuclide product decay begins as soon as they have formed, which leads to the following expression, where the overall rate of production becomes:
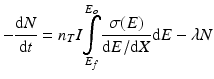
where:
The term dE/dx in the above expression is often referred to as the total stopping power. At a particular energy E, it can be represented as S T (E) in units of MeV · cm2 · g−1 and is given by the following expression:
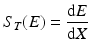
where:
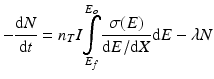
(6.5)
λ is the decay constant and is equal to ln 2/T ½.
t is the irradiation time in seconds.
N is the number of radioactive nuclei in the target.
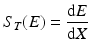
(6.6)
dE is the differential loss in energy.
dx is the differential distance travelled by the particle.
The loss of energy, dE, in MeV of the particle is then given by:
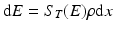
where ρ is the density of the material in units of g/cm3, and the thickness of the target? ρdx (in g/cm2) can be expressed as a function of dE:
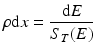
If this equation is integrated to include the stopping power to account for energy loss during the transit of the particle through the target material and assuming that the beam current is the same as the particle flux (which is true only for particles with a charge of +1), then the yield of a nuclear reaction is given by:
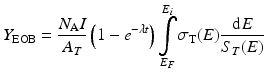
The radionuclide production rate is of course affected by the radioactive decay of the resulting radionuclide product. For short-lived nuclides, the competing reaction rates, production, and decay will achieve equilibrium at sufficiently long bombardment times since the rate of decay is proportional to the number of radionuclide present. The (1 – e –λt ) term is often referred to as the saturation factor and accounts for the competition of the production of nuclei due to the particle reaction and the radioactive decay of the nuclei that have been produced. For an infinitely long irradiation, the saturation factor (1 – e –λt ) tends to the value 1.
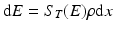
(6.7)
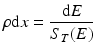
(6.8)
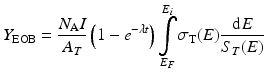
(6.9)
6.3 Key Accelerator-Produced Therapeutic Radionuclides
6.3.1 Actinum-225 and Radium-223
The accelerator production route which involves irradiation of natural 232Th targets with medium-energy protons (Fig. 6.3) appears to be an attractive route in terms of yield and cost-effectiveness.
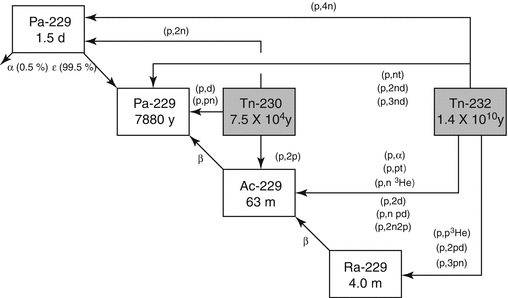

Fig. 6.3
Proton-induced reactions for the production of 229Th
Actinium-225 is of great interest for therapy as well as a generator parent for the availability of 213Bi (Apostolidis et al 2005; Miederer et al 2008; Scheinberg and McDevitt 2011). The scope of availing 225Ac as well as 213Bi for 229Th is schematically depicted in Fig. 6.4.
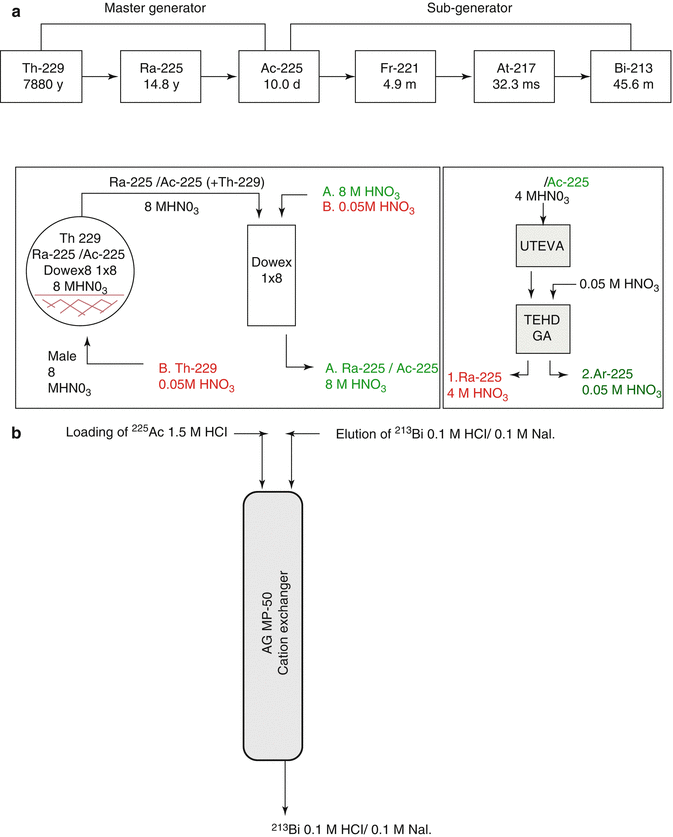

Fig. 6.4
Availability of 225Ac as well as 213Bi from 229Th. (a) Master 229Th/225Ac generator, (b) sub 225Ac/213Bi generator
Chemical isolation of Ra from irradiated metallic Th was performed by a gas-chemical method (Zhuikov et al. 2011). For 225Ac and 223Ra processing following irradiation of natTh targets using 800 MeV protons, solvent extraction with ethyl acetate has been used (Weidner et al. 2012). A method for purification of 225Ac from irradiated 226Ra-targets consisting of a first extraction chromatography for separating 225Ac from 226Ra and other Ra-isotopes and a second extraction chromatography for separating 225Ac from 210Po and 210Pb has been reported. The finally purified 225Ac can be used in the preparation of radiopharmaceuticals (Turlera et al. 2013). This separation scheme is shown in Figs. 6.5 and 6.6.
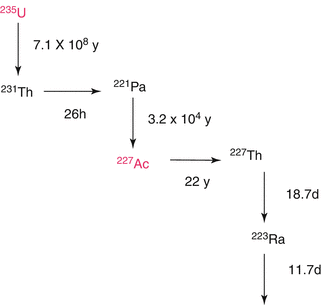
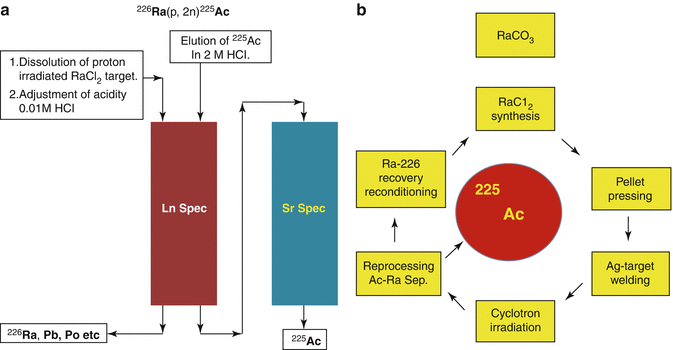

Fig. 6.5
Decay scheme for 223Ra

Fig. 6.6
Production and separation of 225Ac by proton irradiation of 226Ra target
Radium-223 has recently emerged as a key agent for bone pain palliation in castration-resistant metastatic cancer from prostate cancer and is discussed in detail in Chap. 12. An 227Ac/223Ra extraction generator based on selective extraction of 223Ra from a solution of chlorinated cobalt dicarbollide and polyethylene glycol in a polar diluent from a solution of a mineral acid and a complexing agent has been proposed. Radium is stripped to any appropriate aqueous solution on adding TBP into the extractant (Weidner et al. 2012). A number of additional radiochemical separations approaches for the isolation of 223Ra from 227Th have been reported (Henricksen et al. 2001; Horowitz and Bond 2003; Boll et al. 2005; Kirby 1969). While the isolation of high purity 223Ra and 227Th from 227Ac chemically appears to be straightforward, it is mechanically complex due to intense alpha and gamma radiation which produces reactive species (solvated electrons, hydroperoxide ions, atomic hydrogen, and free hydroxyl) that can cause the radiation damage to the ion exchangers and solvents and interfere with radiochemical separations.
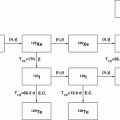
6.3.2 Astatine-211
The radiotherapeutic potential of α-emitting 211As (T 1/2 = 7.21 h) (see Chap. 3) has been recognized for over 30 years (Smit et al. 1973). Astatine in a halogen and the branched pathway for 211As decay is illustrated in Fig. 6.7. The 7.2 h half-life is sufficient to permit multistep synthetic procedures and is also sufficiently long to accommodate for the pharmacokinetics of a wide variety of potential cell-specific targeting agents. The halogen chemistry of astatine is diverse and permits radiolabeling of a wide range of molecules. It is possible to exploit both its metallic characteristics (Milesz et al. 1989; Yordanov et al. 2000) and its halogen properties for the synthesis of 211At-labeled molecules. Astatine-211 decays either directly by α-decay to 207Bi (42 %), followed by EC decay to stable 207Pb, or by EC decay to 211Po (58 %), followed by α-emission to stable 207Pb. The α particles have a range of only 55–80 μm in biological soft tissue, which represents only a few cell diameters. The high mean LET value of about 100 keV/μm is close to the optimum value for a high RBE to maximize the lethal damage (Zalutsky and Bigner 1996). The 211Po daughter emits 77–92-keV X-rays that provide a valuable means for tissue tracking 211At by SPECT imaging (Johnson et al. 1995). With regard to radiation protection issues, 211As is easy to handle, since α particles represent more than 99 % of the radiation energy (Larsen et al. 1999).
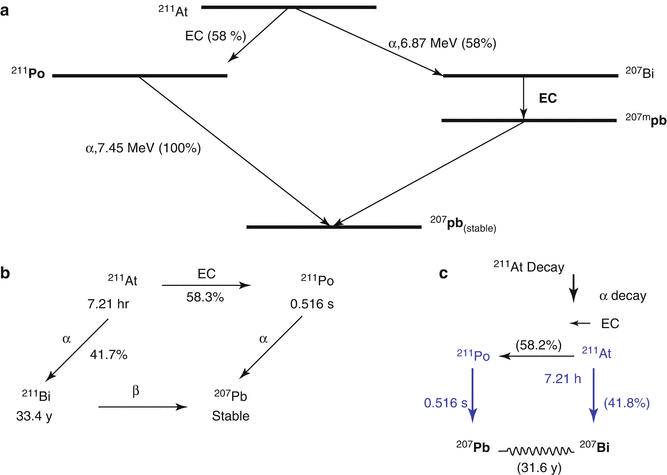

Fig. 6.7
Simplified decay scheme of 211At
Spallation reactions can be useful for 211At production either directly or indirectly through the decay of 211Rn, but the required high particle energies between 160 and 660 MeV and limited beam intensity, in addition to the extensive required separation procedures, emerged as major impediments for the use of this strategy for routine production required to meet expected clinical demands (Kirby 1985). Currently, the most commonly used method for producing 211At is the bombardment of natural bismuth, usually in metallic form, with α particles (Zalutsky and Pruszynski 2011). Although the use of natural bismuth constitutes an ideal target material in terms of cost-effectiveness and precludes the need for chemical recovery for its subsequent use, its poor thermal conductivity (7.97 W · K−1 · m−1) and low melting point (272 °C) necessitates adequate target cooling at high current production runs.
The purity of 211At required for research and clinical studies is influenced by the radiochemical procedures adapted for the recovery of 211At from the bismuth cyclotron target. Although a variety of methods have been reported for 211At recovery (Eberle 1985), the most common method involves dry distillation or acid treatment of the target followed by solvent extraction. The most commonly utilized approach for separating 211At from bismuth cyclotron targets is dry distillation at a temperature range of 650–800 °C for 30 min using a flow of carrier gas such as nitrogen (Lidegren 2001) or argon (Zalutsky 1996) in a quartz vessel. After volatilization from the cyclotron target, 211At can be trapped using silica columns (Friedman et al. 1977), bubbler traps (Lindgren 2001), and capillary tubing cryotraps (Lambrecht and Mirzadeh 1985). The solvent extraction procedure consists of dissolution of target using concentrated HNO3 followed by extraction of 211At into either butyl or isopropyl ether (Yordanov et al. 2004). Another approach reported is based on dissolution of the Bi2O3 target in concentrated perchloric acid followed by solid–liquid extraction employing thiosemicarbazide incorporated onto Amberlite IRC-50 resin (Roy et al. 2004).
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree