Abstract
Magnetic resonance imaging (MRI) and specifically diffusion MRI opened, for the first time, a window into the in vivo physiology of white matter. Almost two decades ago, diffusion tensor imaging (DTI) provided the ability to reconstruct and characterize white matter pathways. Despite the fundamental new insights it provides, DTI has several limitations reducing the specificity and interpretability of derived indices (mean diffusivity and fractional anisotropy). Newer diffusion MRI-based frameworks such as CHARMED, AxCaliber, and ActiveAx allow more detailed investigation of white matter microstructure through the modeling of the diffusion signal. These frameworks allow extraction of more detailed microstructural parameters such as the axonal density and axonal diameter distribution. This chapter will describe the theoretical background as well as experimental aspects of the recent diffusion MRI frameworks and their potential application in the spinal cord.
Keywords
Axon density, Axon diameter, Diffusion MRI, Myelin, White matter
3.3.1
Introduction: Diffusion Imaging and Tissue Microstructure
Diffusion imaging and particularly diffusion tensor imaging (DTI) have become standard tools for assessment of white matter in the brain. Although somewhat more technically challenging to implement in the spinal cord, these methods are now also commonplace in studies of the spinal cord.
DTI provides two unique pieces of information over any preceding method. First, it provides an estimate of the dominant orientation of local fibers in each image voxel. That information is the foundation of tractography and structural connectivity mapping in the brain. In the spinal cord fiber orientation information is less useful, since the fiber structure is simpler and generally predicted quite easily, but disruptions to that structure may still be important in injury or disease.
The second key information from DTI is a set of orientationally invariant indices, e.g., fractional anisotropy (FA) and mean diffusivity (MD) that provide crude, but useful, markers of microstructural integrity. These quantitative parameters have been used widely in the brain, spinal cord, and peripheral nervous system, as well as a range of other organs and tissue types. For a full description of DTI theory and application to the spinal cord, see Chapter 3.1 .
In recent years, some drawbacks in both these unique aspects of DTI have become increasingly evident. The DT model provides only a single fiber orientation in each image voxel and fails in areas of heterogenous white matter such as fiber crossings. Crossing fibers are less widespread in the spinal cord, where the white matter is more regularly ordered, but crossings and other complex fiber configurations do occur. Moreover, the simple DTI microstructure indices lack specificity. White matter contains several cellular components (cells, axons, myelin), each with its own dimensions, density, and other properties that affect water mobility. Simple parameters such as the FA or MD provide only a very crude description of the complex environment that summarizes many different effects. The recent trend in diffusion imaging has been to develop more sophisticated models that enable estimation of these different components individually to provide more specific information on the geometry and physiology of white matter tissue. This chapter summarizes the state of the art for studying white matter through diffusion and speculates on their potential in the spinal cord.
3.3.2
Advanced Methods for Studying White Matter
As the b -value increases, the DT model rapidly becomes inadequate to explain diffusion measurements from white matter. Significant departures occur even at b = 1000 s/mm 2 in vivo. These departures indicate a non-monoexponential decay of the signal arising from complex diffusion processes in multiple compartments. The existence of non-Gaussian diffusion in neuronal tissue has motivated over the last decade several innovations in data acquisition and analysis to capture and exploit the extra information in the signal to estimate more useful tissue features. These methods divide into two groups: (1) model based and (2) model free. While all approaches assume some kind of underlying signal model, the classification refers to the use (or not) of a biophysical model with parameters reflecting specific tissue properties. For a detailed treatment of the model-free methods, see Chapter 3.2 .
3.3.2.1
Model-Free Techniques
The simplest model-free approach is q -space imaging (QSI), often referred to in 3D as diffusion spectrum imaging (DSI). For an extensive treatment of q -space theory and applications, see also Chapter 3.2 . This kind of analysis relies on the very basic signal model in which the diffusion-weighted signal is the Fourier transform of the diffusion propagator. By varying the length, strength, and orientation of the gradient pulses in the diffusion imaging acquisition sequence, we can sample the signal at various wavevectors. QSI and DSI work by acquiring a set of measurements typically with wavevectors in a grid configuration and inverting the Fourier transform to obtain a discrete representation of the diffusion propagator.
Several parameters can be extracted from such analysis. If measured along a particular direction, the displacement distribution function can be characterized by its width (mean displacement < D >) and height (probability for zero displacement P 0 ). These parameters were found to be extremely useful for characterization of the human brain and excised spinal cords (see section 3.3.3 following). If the QSI experiment is done in 3D, as in DSI, the analysis provides the diffusion orientation density function (ODF) by projecting the propagator onto a sphere via a radial integration. This ODF has peaks in each of potentially many different fiber directions, so provides a better basis for tractography than DTI.
For tractography alone, DSI is uneconomical in terms of acquisition time, and various other methods try to estimate the diffusion ODF and related functions from more economical high angular resolution diffusion imaging (HARDI) acquisition; see for a review. Q-ball imaging uses the Funk–Radon transform as an approximate mapping from HARDI data to the diffusion ODF. PAS-MRI estimates a diffusion ODF with greater sensitivity to fiber orientations. Spherical deconvolution techniques combine the model-based techniques described in the next section with a model-free description of the ODF to obtain a fiber ODF. See Ref. for an explanation and comparison of these various ideas.
Hybrid diffusion imaging (HYDI) provides a framework to estimate all of the common DSI parameters, including < D >, P 0 , and the diffusion ODF, from multishell HARDI data, which is more economical than full DSI. Diffusion kurtosis imaging (see also Chapters 3.1 , Chapters 3.2 ) uses multishell HARDI and estimates an additional parameter, the diffusion kurtosis tensor, which characterizes the departure from the Gaussian model used in DTI.
All these parameters are useful markers of tissue integrity that often provide complementary information to the basic DTI indices. However, they remain nonspecific and difficult to associate with specific features of the tissue microstructure.
3.3.2.2
Model-Based Techniques
The model-based approaches include several frameworks with increasing complexity of the model. The most basic model includes a multiexponential decay function, anomalous diffusion, or a stretched exponential function. Such models can adequately characterize the deviation from Gaussian diffusion, such as the non-Gaussian diffusion that stems from restricted diffusion, in a similar way to model-free techniques like diffusion kurtosis. A biophysical interpretation can be attached to some parameters; for example, associating a separate tissue compartment to each exponential component provides an estimate of the orientation and volume fraction of each compartment.
More directly, biophysical models employ a geometric description of the tissue compartments and exploit restricted diffusion as a window on the geometry. These models are built from assumptions on the diffusion properties of water in different compartments of the tissue. For example, Stanisz et al. proposed a model with three compartments: axonal, glial, and extracellular space. The axons are elongated ellipsoids, and the glia are spherical. Each has a semipermeable membrane and unique volume fractions and internal diffusivity. The composite hindered and restricted model of diffusion (CHARMED) assumes that the diffusion within axons is restricted perpendicular to the axons, while elsewhere (cells, extra cellular matrix, and parallel to the axons) it is hindered or free. The minimal model of white matter diffusion (MMWMD) combines elements of both CHARMED and Stanisz’s model in an attempt to identify the simplest model that explains diffusion data from white matter. Zhang et al., following the earlier work of Jespersen et al. and Kaden et al., extend the MMWMD to include fiber orientation dispersion, which is another significant influence on the signal. Panagiotaki et al. define a taxonomy of models for diffusion in white matter, which relates all those mentioned herein within a broader framework of compartment models and performs a statistical comparison of their ability to explain measured signals.
From such models parameters such as the axonal density, diameter distribution, and intra/extra cellular diffusivity can be estimated and mapped. The models also extend to include other parameters such as cell permeability and shape. However, the modeling process rapidly becomes complex and the number of parameters increases rapidly rendering estimation ill posed if signal-to-noise ratio is not sufficient (as is likely in high b -value diffusion imaging). Despite that, successful demonstrations and systems are now in the literature. For example, the restricted diffusion volume fraction (axonal density) maps from CHARMED analysis were found to be extremely useful and sensitive in the brain and provide an alternative to FA that relates more specifically to axon density. The Neurite Orientation Dispersion and Density Imaging (NODDI) technique extends the set of specific parameters to include indices of fiber orientation dispersion and CSF volume fraction, thus separating the three key parameters that influence FA in brain imaging.
AxCaliber, an application of CHARMED, models, aside from axonal density, can also estimate the axon diameter distribution. The model assumes that this distribution has a gamma function shape. Based on a multi diffusion time experiment where in each diffusion time a different population of axons will experience restricted diffusion, the estimation of the gamma function becomes feasible. This method was demonstrated on the rat corpus callosum and on excised spinal cord (see following).
The ActiveAx technique uses the MMWMD together with an optimized multishell HARDI acquisition protocol to map an axon diameter index over the brain. The simple model and optimized experiment design enable the technique to be orientationally invariant. Thus, unlike earlier techniques, which require the fiber to have known and fixed orientation, ActiveAx provides indices for fibers in all orientations from a single acquisition. However, the index provided is less quantitative than the AxCaliber axon diameter distribution because it provides only a single summary statistic of the full distribution. In theory, the axon diameter index reflects the average axon diameter weighted by axon volume, although there are some departures from this complicated interpretation. Nevertheless, in fixed monkey brains using data from a 4.7 T high field scanner with 140 mT/m and 300 mT/m, the technique provides maps that reflect what we expect from histology. In vivo human results are noisier, but an ROI analysis also reflects the expected trends. As an alternative to ActiveAx, Barazany et al. suggested an extension of AxCaliber into 3D to allow estimation of the full axon diameter distribution function for any orientated fiber system.
While current axon diameter estimation techniques show good results in experimental animal systems with high gradients available, on human systems they largely remain scientific demonstrations rather than tools for large-scale studies; the human data sets in Alexander et al. took over 1 h to acquire. Further work is required to realize the potential of these techniques for human studies. Modeling advances, such as those described in Panagiotaki et al. and Zhang et al. make incremental but significant improvements. Greater advances are likely to come from improvements in data acquisition to increase sensitivity to the specific parameters of interest. For example, oscillating gradients and generalized waveforms can provide orders of magnitude more sensitivity to small axon diameters. Exploitation of such pulse sequences potentially offers much greater sensitivity and practical axon diameter mapping techniques for human studies in the near future.
In the spinal cord, the orientational invariance of ActiveAx is less of an advantage than in the brain because of the simpler orientational structure of the cord. However, the model and experiment design optimization that underpin the technique also provide advantages when the orientation is known; Schneider et al. demonstrate this in the corpus callosum, and that extension is directly applicable to the spinal cord. Measures of orientation dispersion from NODDI are likely to find use in the spinal cord as well as the brain both for studying the intersections of peripheral nerves with the cord, where orientation dispersion can be significant, and for pinpointing different kinds of pathology more precisely. The benefits of alternative pulse sequences are equally applicable in the spinal cord and will help provide more precise information in more manageable acquisition times as these techniques develop.
3.3.3
Applications in Spinal Cord
- •
QSI in the spinal cord (see also Chapter 3.2 )
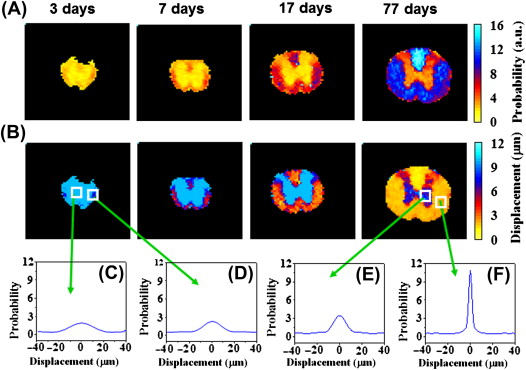
QSI is a model-free approach that can characterize diffusion MRI signal measured at a wide range of b value. Being a model-free framework, the extracted parameters also have a vague meaning. From the displacement distribution function two parameters are extracted: the mean displacement (< D >) and the probability for zero displacement ( P 0 ). Although these two parameters are not particularly specific to any diffusing component in the tissue, it is assumed that if the experiments are done at sufficient high b values (>10,000 s/mm 2 ) and exactly perpendicular to the fibers, these two parameters (< D > and P 0 ) represent mostly restricted diffusion. Some support for this assumption comes from experiments on excised optic nerve where it was shown the < D > does not change when increasing the diffusion time indicating restricted diffusion (probably within the axons).
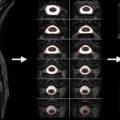
This method was applied first on two studies in the spinal cord: (1) a development study ; (2) a degeneration study.
In the development experiment, excised spinal cords of rats at different ages (from postnatal day 3 to adulthood) were scanned with QSI protocol. It was shown that the < D > reduces with age while the P 0 increases, indicating increase in restricted diffusion with age (probably due to myelination) ( Figure 3.3.1 ). While this observation accompanies FA changes with age (increase with myelination) it seems that changes in < D > are much more dramatic and span over a much broader range of values increasing the sensitivity of this parameter.