Assessment of the Biophysical Mechanical Properties of the Arterial Wall

Arteries are elastic tubes whose diameter varies with the pulsating pressure. In addition, they propagate the pulse created by ejection of blood by the heart, at a velocity that is determined largely by the elastic properties of the arterial wall. The vascular wall can be deformed by pressure and shear stress forces exerted by the blood as well as the tethering imposed by the surrounding tissues. Biophysical mechanical properties of the arterial wall play an important role in the pathogenesis of cardiovascular diseases. Sclerosis (or stiffness), for example, is an important aspect of atherosclerotic vascular disease that can be demonstrated in experimental disease both in animals and in humans, and regression of the disease leads to reduced stiffness. Rupture of atherosclerotic plaque (a common mechanism of myocardial infarction) and aortic dissection can be viewed as mechanical failures in the diseased vessels. In addition, the effectiveness of interventional procedures such as angioplasty is often achieved by causing mechanical injury to the vessel wall, and the injury itself may lead to restenosis. A number of common conditions are associated with changes in arterial mechanical properties, although their importance is not always recognized.

Systemic hypertension is almost always associated with altered mechanical properties of the peripheral vasculature. Although it is not clear which of the two is the inceptive event, one begets the other, fostering a vicious cycle. Compliance (the reciprocal of the resistance offered to deformation) of the proximal aorta is reduced as a result. This causes waves reflected from the periphery to return prematurely and coincide with the incident or forward-traveling wave produced by the ventricle. This augments aortic systolic pressure, increases pulse pressure, and reduces diastolic pressure (because the reflected wave no longer contributes to diastolic pressure). Decreased subendocardial/subepicardial flow ratio has been demonstrated with reduced aortic compliance. Thus decreased aortic distensibility may increase the risk of subendocardial ischemia in the presence of coronary artery stenosis, left ventricular hypertrophy, or both.

Aortic compliance represents an important determinant of left ventricular performance. Measurement of ventricular–vascular coupling takes into account the pulsatile load imposed on the left ventricle, as well as the systemic vascular resistance. Metabolic disorders such as Ehlers–Danlos and Marfan syndromes, diabetes mellitus, familial hypercholesterolemia, and growth hormone deficiency are also known to alter arterial compliance.

Similarly, the distensibility of the pulmonary arteries is reduced in pulmonary hypertension. Postmortem studies of externalized pulmonary arterial strips have shown that the extensibility of the pulmonary trunk is decreased in pulmonary arterial hypertension. The wall of an artery becomes less extensible, the more it is stretched from its natural length. An increased stretching of the circumference of the vessel will diminish the distensibility. When the pulmonary artery resistance increases in vivo, the vessels become more distended and less distensible. Indirect measurements of pulmonary artery compliance have suggested that pulmonary arterial distensibility decreases with rising pulmonary artery pressure. The ability of cardiovascular magnetic resonance (CMR) to image flow within any medium-sized vessel in any plane provides a unique opportunity to study the pulmonary arteries. Distensibility and flow have already been assessed in patients with pulmonary arterial hypertension.

In this chapter, the clinical importance of arterial biophysical function and its assessment by CMR will be examined in detail as a complement to Chapter 27 .

Arterial Structure

A normal artery consists of three morphologically distinct layers. The intima consists of a single continuous layer of endothelial cells bounded peripherally by a fenestrated sheet of elastic fibers. The media consists entirely of diagonally oriented smooth muscle cells, surrounded by variable amounts of collagen, elastin, and proteoglycans. The adventitia consists predominantly of fibroblasts intermixed with smooth muscle cells loosely arranged between bundles of collagen and proteoglycans. Each structural component has its own characteristic properties. Smooth muscle is the physiologically active element, and by contracting or developing force, it can alter the diameter of the vessel or the tension in the wall. The other components are essentially passive in their mechanical behavior. Elastin, which can be stretched to up to 300% of its length at rest without rupturing, behaves mechanically more closely to a linear elastic material such as rubber than other connective tissue components do. When elastin fibers are stretched and released, they return promptly to their original state. Elastin fibers are important for maintaining normal pulsatile behavior, but they fracture at very low stresses and are probably much less important in determining the overall strength of the vessel wall. Collagen fibers, on the other hand, are much stiffer, but they are much stronger. The proportion of these components varies from artery to artery. In the thoracic aorta, the elastin forms 60% of total fibrous element, and collagen forms 40%. The collagen proportion increases with increasing distance from the heart, reaching 30% elastin and 70% collagen in the extrathoracic vessels. The collagen-to-elastin ratio increases with age, which is one reason why vascular stiffness increases with age. The human thoracic aorta is supplied by vasa vasorum and grows by increasing the number of lamellar units. The abdominal aorta, in comparison, is avascular because it lacks vasa vasorum and grows by increasing the thickness of each lamellar unit. The avascular thickness and the elevated tension per lamellar unit of the abdominal aorta predispose it to atherosclerosis.

The distensibility of a blood vessel depends on the proportions and interconnections of these materials and on the contractile state of the vascular smooth muscle. Elasticity is a material’s ability to return to its original shape and dimensions after deformation, the deformation being proportional to the force applied. This proportionality was first described by Hooke in 1676 and is known as Hooke’s law. The point at which Hooke’s law ceases to apply is known as the elastic limit, and when a solid has been deformed beyond this point, it cannot regain its original form and acquires a permanent distortion. With larger loads still, the yield point is reached when the deformation continues to increase without further load and usually rapidly leads to breakage. In purely elastic bodies, stress (the force per unit area that produces deformation) produces its characteristic strain (the deformation of a stressed object) instantaneously, and strain vanishes immediately on removal of the stress. Some materials, however, require a finite time to reach the state of deformation appropriate to the stress and a similar time to regain their unstressed shape. Blood vessels typically exhibit such behavior, which is called viscoelasticity.

Definition of Vascular Wall Stiffness

Vascular mechanics have been described by using different elastic moduli and assumptions and for different purposes. Several approaches have been described that use clinically available methods for in vivo characterization of the stiffness of the vessel wall. The ability to measure vascular stiffness has been greatly improved by the recent advances in imaging, such as high-frequency ultrasound and CMR.

The relationship between vascular wall deformation (strain) and the pressure exerted on the inner surface of the vascular wall (stress) is commonly used for the measurement of arterial wall biophysical properties (elastic modulus). A plethora of terminology for the description of different elastic moduli, which can be confusing, has been described. The pressure–strain elastic modulus of the arterial wall ( E _p ) described by Peterson and colleagues is commonly used. This elastic modulus that applies to an open-ended vessel in the absence of reflection is defined as E _p = 2Δ P /(Δ V / V ). This is the inverse of the fractional distensibility Δ V / V of the arterial lumen per unit pulse pressure Δ P .

Arterial compliance, C , which is defined as the change in volume Δ V per unit change in pressure Δ P , has been also used in the literature. It has been argued that this definition is appropriate to measurement of ventricular compliance and not to the compliance of an open-ended arterial segment. For the latter, the inverse of Peterson’s modulus was suggested 1/ E _p .

The average arterial compliance of a particular vessel pathway can also be determined by measuring the speed of propagation of the pulse in the vessel pathway. The velocity of such waves depends principally on the distensibility of the vessel wall. In real terms, this pulse is measurable by the disturbances in pressure, flow, or vessel diameter that it causes. The propagation of flow waves has not been studied as extensively as that of pressure waves, partly because, unlike flow, accurate methods of pulsatile pressure measurements have been available for a long time and partly because the distinction between flow wave velocity and blood velocity has not always been clearly recognized. Blood velocity means the speed of an average drop of blood, whereas flow wave velocity means the speed with which motion is transmitted. The wave velocity is usually much faster than that of the blood itself. Although CMR is unable to assess pressure changes, alterations in the flow within (or diameter of) a vessel can be measured accurately.

Measurement of Arterial Wall Stiffness

Arterial stiffness, which describes the resistance of arterial wall to deformation, is difficult to measure because of the complex mechanical behavior of arterial wall. As a result, a bewildering number of choices abound. Although smooth muscle tone is not considered, in vitro human arterial compliance has been measured from pressure–volume curves in postmortem arteries. In vivo estimation of arterial wall compliance is more difficult, however, and has been performed by using indirect and invasive techniques, including pulse wave velocity measurements in animals and in humans, the pressure–radius relationship using the Peterson transformer coil in animals, x-ray contrast angiography in humans, and ultrasonography. The contributions of CMR to the assessment of arterial wall mechanics are discussed in the following paragraphs. Other noninvasive measures are forced to rely on the assessment of accessible and often superficial vessels. Under the assumption that central and peripheral arteries behave in a similar fashion, the properties of these arteries are then used as surrogates for those of central arteries. There is, however, considerable heterogeneity between peripheral and central sites. CMR circumvents this problem by allowing the study of central arteries. Its ability to identify anatomic landmarks suggests that reproducibility between studies should be improved, allowing more effective follow-up.

Cardiovascular Magnetic Resonance of Regional Aortic Compliance

CMR provides a direct, noninvasive way of studying local aortic compliance. High-resolution cine imaging or electrocardiogram-gated spin echo imaging in a plane perpendicular to the ascending and/or descending aorta allows measurement of aortic cross-sectional area during systole and diastole. Measurement of regional aortic compliance by CMR is calculated from the change in volume of an aortic segment and from aortic pulse pressure estimated by a sphygmomanometer at the level of the brachial artery. The lumen of the aorta is outlined manually on the computer screen to measure the change in aortic area (ΔA) between diastole and systole. Regional aortic compliance (C) (microL/mm Hg, m ³ /Nm ⁻² ) is calculated from the change in volume ( ΔV = ΔA × slice thickness) of the aortic segment divided by the aortic pulse pressure (ΔP) measured by a sphygmomanometer ( Fig. 29.1 ). Automatic measurement of aortic cross-sectional area is also possible. Other indices of aortic stiffness that can be derived from these measurements include distensibility, Peterson’s elastic modulus, and stiffness index β ([systolic blood pressure/diastolic blood pressure]/area strain).

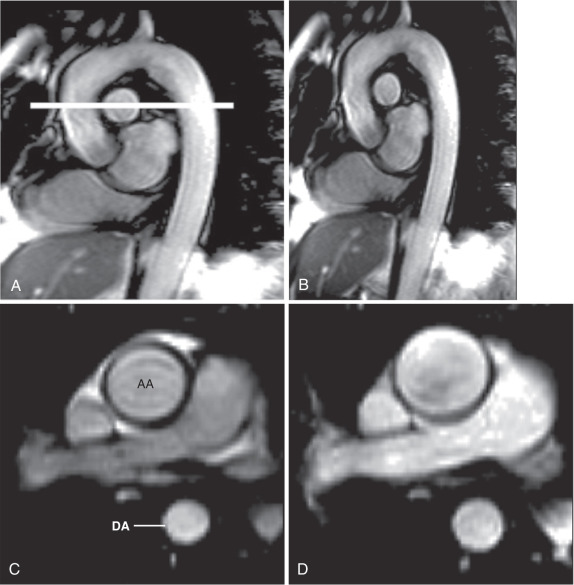
The accuracy of the indirect measurement of the pressure change that is needed to compute compliance is limited because it ignores the changes in the pressure wave as it propagates through the arterial tree (a process known as amplification). Further, it is important to obtain this pressure data on patients who are ideally lying in the magnetic resonance imaging (MRI) scanner using CMR-compatible apparatus. Despite the limitations of the pressure measurement, there is a good correlation between measurement of local aortic compliance and measurement of global compliance from the speed of the propagation of the flow wave within the vessel.

In addition, noninvasive pressure wave analysis using arterial applanation tonometry has been shown to provide an accurate and reproducible measurement of central vascular pressure measurements and can be used to overcome this limitation.

Cardiovascular Magnetic Resonance of Flow Wave Velocity

Flow wave velocity is defined as the speed with which a flow wave propagates along a vessel and is regarded as the purest measure of arterial stiffness. It is the quotient of distance traveled divided by the time taken for the flow wave to move between the two points and represents an average for that length of vessel ( Figs. 29.2 and 29.3 ). The approach is dependent on assessment of path length traveled and accurate measurement of pulse arrival time. The latter requires recognition of equivalent features or points on leading edges of the proximal and distal flow waveforms (see Fig. 29.2 ), a process that is made complicated by alterations that occur in flow wave morphology and magnitude as it progresses down the vessel. Unlike noninvasive measurements that rely on linear, transcutaneous measurements, CMR makes no assumptions about the shape of the artery and can accurately measure the path length traveled.

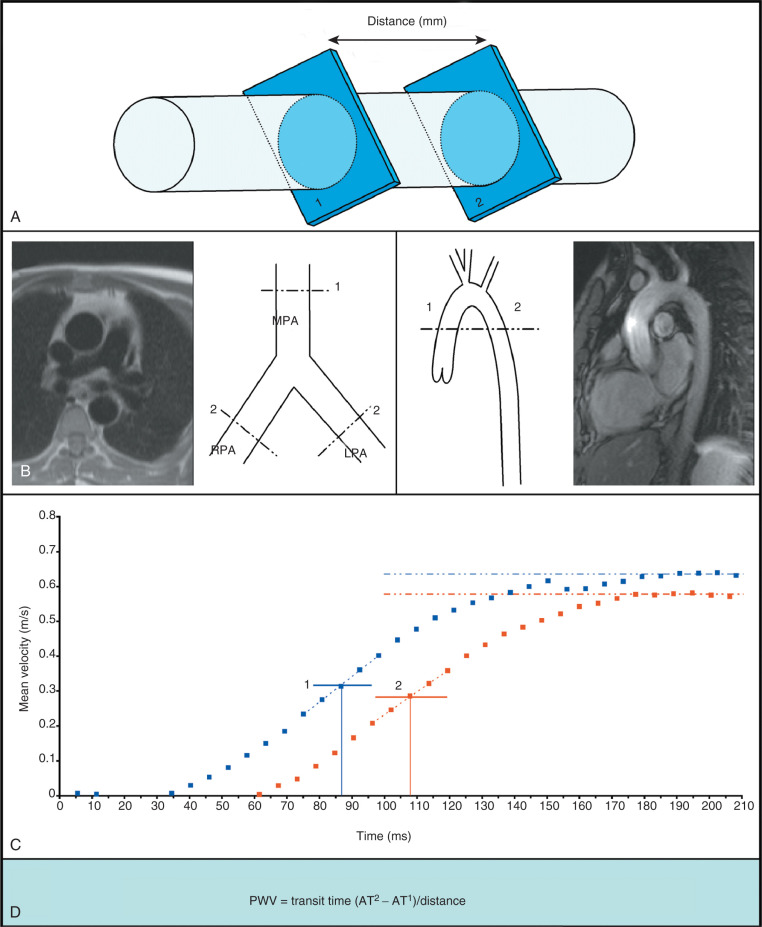
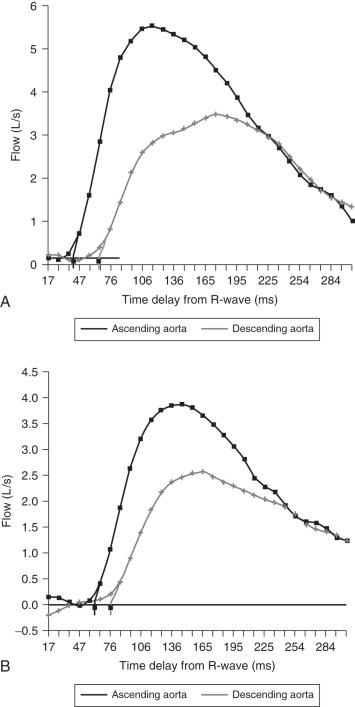
Mohiaddin and colleagues showed the feasibility of using CMR phase-shift velocity mapping to measure aortic flow wave velocity in humans. By taking advantage of the anatomy of the aorta, cine two-dimensional (2D) phase shift velocity maps were acquired with high temporal resolution in a single plane perpendicular to the ascending and descending aorta, and the time taken for the flow wave to travel between the two points was measured ( Fig. 29.4 ). Instantaneous flow (in liters per second) in the mid-ascending aorta and mid-descending aorta was calculated by multiplying the aortic cross-sectional area and the mean velocity within that area. Pulse wave velocity (PWV) was calculated in meters per second from the transit time (T) of the foot of the flow wave (see Fig. 29.4 ) and from the distance (D) between the two points obtained from an oblique sagittal image. The distance is determined manually on the computer screen by drawing a line in the center of the aorta joining the two points. In Fig. 29.4 , the foot of the flow wave was defined by extrapolation of the rapid upstroke of the flow wave to the baseline as opposed to the midpoint of the upslope method used in Fig. 29.2 .

Others have used different magnetic resonance flow imaging techniques to assess arterial compliance. Tarnawski and colleagues used the comb-excited Fourier velocity-encoded method, previously reported by Dumoulin and colleagues, to measure local arterial wave speed in the femoral artery in healthy men. In this method, simultaneous Fourier velocity-encoded data from multiple stations were acquired. The technique employs a comb excitation radiofrequency pulse that excites an arbitrary number of slices. This causes the signals from the spin in a particular slice to appear at a position in the phase-encoding direction, which is the sum of the spin velocity and an offset arising from the phase increment given to that excitation slice. Acquisition of spin velocity information occurs simultaneously for all slices, permitting the calculation of wave velocities arising from the pulsatile flow.

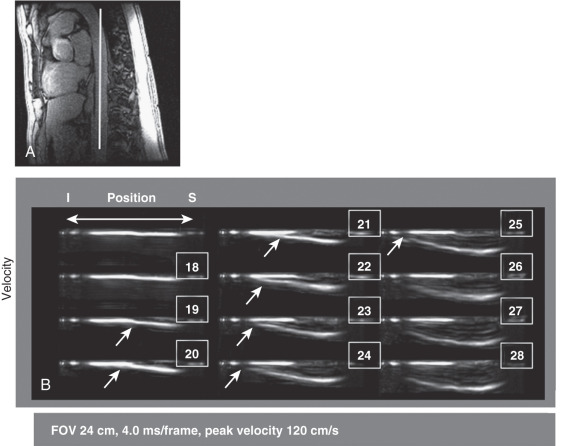
Hardy and colleagues studied aortic flow wave velocity using a 2D CMR selective excitation pulse to repeatedly excite a cylinder of magnetization in the aorta, with magnetization readout along the cylinder axis each time. A toggled bipolar flow-encoding pulse was applied before readout to produce a one-dimensional (1D) phase-contrast flow image. Cardiac gating and data interleaving were employed to improve the effective time resolution to 2 ms. Wave velocities were determined from the slope of the leading edge of flow measured on the resulting M-mode velocity image. Aortic pulse wave velocity was also measured by the same group, using a combination of cylinder of magnetization with Fourier velocity encoding and readout gradients applied along the cylinder axis (aorta) ( Fig. 29.5 ), with the advantage of eliminating partial volume effects that hindered their previous approach, but the Fourier method has the drawback that it is no longer in real time and errors occur, owing to accumulation of flow data over several (typically 16 to 32) cardiac cycles. For both methods, the interleaved repeats needed to achieve high temporal resolution make them highly sensitive to physiologic variability.

In vitro experiments showed CMR measurements of pulse wave velocity in a tube phantom to be very reproducible and in good agreement with pulse wave velocity measurements made with a pressure catheter. These methods have not been widely applied in clinical research, nor has their in vivo reproducibility been proven yet.

Reflected Waves

When the incident pulse wave from the ventricle reaches the periphery, it may be reflected and return toward the heart as a backward-running wave. Reflected waves express properties of the peripheral circulation; if the peripheral resistance is elevated, reflected waves will be greater in magnitude and will return sooner. Because its shape and magnitude will be defined by the complex interaction between forward incident wave and backward reflected waves, the measured flow wave will also be altered in pathologic conditions. As a result, the timing and location of measurements become important considerations in the CMR assessment of arterial properties.

If work is concerned only with the structure of proximal arteries, measurement should be made as far from the periphery and as early in systole as possible to avoid the influence of reflections. These requirements become more demanding when the available length of vessel is limited (e.g., in the pulmonary arteries) or baseline data particularly noisy. Conversely, study of the influence of reflected waves on measured flow waves might provide interesting insights into the nature of the more distal vessels .

Clinical Use of Cardiovascular Magnetic Resonance for Assessing Arterial Wall Stiffness

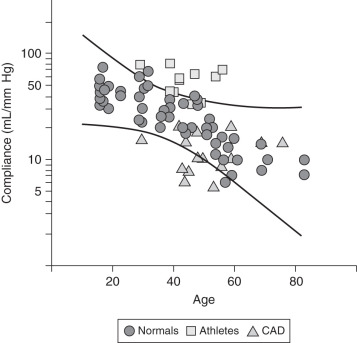
Mohiaddin and colleagues were the first to use CMR for measurement of aortic compliance. They demonstrated that aortic compliance in asymptomatic subjects falls with age and that patients with coronary artery disease have abnormally low compliance ( Fig. 29.6 ). The results suggested a possible role for compliance in the assessment of cardiovascular fitness and the detection of coronary artery disease. Because there is overlap between normal compliance and compliance in patients with coronary artery disease above the age of 50 years, the test cannot have perfect sensitivity and specificity. Below the age of 50 years, however, there is much less overlap and the test is more specific. Abnormally low aortic compliance has also been demonstrated in patients with aortic coarctation and in patients with Marfan syndrome. The same group also showed the feasibility of using CMR velocity mapping for measurement of aortic flow wave velocity. Aortic flow wave velocity increased linearly with age, and there was a significant difference between the youngest decade and the oldest decade studied. Flow wave velocity was negatively correlated with regional ascending aortic compliance measured in the same subjects ( Fig. 29.7 ).