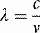Chapter 1 Atoms, nuclei and radioactivity
Introduction
The smallest identifiable amount of an element is an atom, consisting of a central nucleus composed of protons and neutrons which is orbited by electrons. The diameter of an atom and nucleus are typically 10−10 m and 10−14 m, respectively. To put these dimensions into a more accessible perspective, if the atomic nucleus is represented by the point of a pencil (diameter approximately 0.5 mm) held in the centre of a medium-sized room (say, 5 m × 5 m), then the electron cloud surrounding the nucleus would extend to the walls of the room. Most of the volume the atom occupies therefore consists of empty space, which makes it relatively easy for uncharged particles, such as photons, to pass through an atom without undergoing any interaction. An atom of carbon has six protons and six neutrons in the nucleus, surrounded by six electrons. Protons and neutrons have almost the same mass, while electrons have a mass roughly 2000 times smaller (shown in Table 1.1). The atomic nucleus therefore occupies a minute fraction (10−10 %) of the atomic volume, yet contains more than 99.9% of the atom’s mass. Electrons and protons each carry the same magnitude of electric charge (1.602 × 10−19 Coulombs), but of opposite sign. The difference in the observed interactions of electrons and protons is therefore mostly due to their different masses: Electrons are relatively light, so scatter easily in a material while protons are less easily scattered.
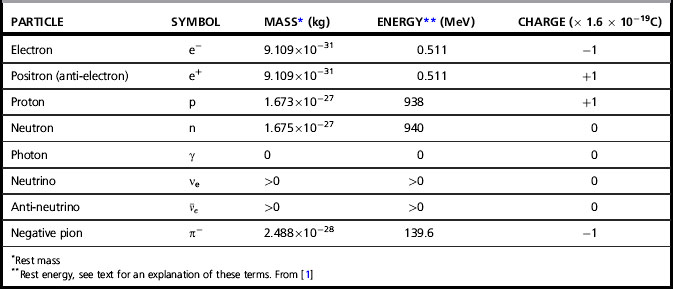
Table 1.1 lists properties of subatomic particles of relevance to radiotherapy. Strictly, only the electron, positron and neutrinos (ν and 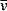 ) are fundamental particles, while protons, neutrons and pions are composed of quarks. Atoms are composed of just electrons, protons and neutrons. The positron is the anti-particle of the electron (having the same mass but opposite charge) and is emitted during beta decay (β+) and in interactions of high energy photons with matter (see pair-production, Chapter 2). The annihilation of a positron with an electron provides the mechanism for positron emission tomography (PET). Neutrinos are uncharged particles of very small mass emitted during beta decay, sharing the energy released from the decay with the emitted beta particle (β+ or β−). Negative pions (π−), one of the triplet of pions (π0, π+, π−) are found in cosmic rays and are thought to be carriers of the strong force between nucleons. Despite their short life time (2.6 × 10−8 s), beams of these particles generated in physics laboratories have been used for radiotherapy treatment, due to their favourable energy-deposition characteristics. This is discussed briefly in Chapter 2.
) are fundamental particles, while protons, neutrons and pions are composed of quarks. Atoms are composed of just electrons, protons and neutrons. The positron is the anti-particle of the electron (having the same mass but opposite charge) and is emitted during beta decay (β+) and in interactions of high energy photons with matter (see pair-production, Chapter 2). The annihilation of a positron with an electron provides the mechanism for positron emission tomography (PET). Neutrinos are uncharged particles of very small mass emitted during beta decay, sharing the energy released from the decay with the emitted beta particle (β+ or β−). Negative pions (π−), one of the triplet of pions (π0, π+, π−) are found in cosmic rays and are thought to be carriers of the strong force between nucleons. Despite their short life time (2.6 × 10−8 s), beams of these particles generated in physics laboratories have been used for radiotherapy treatment, due to their favourable energy-deposition characteristics. This is discussed briefly in Chapter 2.
The electron mass’s energy-equivalence of 8.187 × 10−14 J therefore equals 511 000 eV or 0.511 MeV, as shown in Table 1.1. Mass, m, in equation 1.1 is strictly relativistic mass, which increases as a particle’s speed approaches the speed of light according to Einstein’s theory of special relativity. The notation, m0, generally refers to the concept of constant mass that we are more familiar with, corresponding to that of a particle at rest (rest mass) and the quantity m0c2 is then the corresponding energy associated with the particle (rest energy). The terms rest-energy and rest-mass are commonly interchangeable and both quoted in terms of energy.
The conversion of mass to energy and vice versa is demonstrated in pair-production and annihilation (Chapter 2), where the energy of an incident, mass-less photon is converted into the mass and kinetic energy of an electron and positron pair. The positron eventually annihilates with an electron (its anti-particle), releasing the combined rest mass of both particles, and any remaining kinetic energy, in the form of photons.
Atomic structure
Electromagnetic force
Where k is a constant, e is the electronic charge and Z the atomic number (number of protons) of the atom concerned. This inverse-square relationship is analogous to the gravitational force between two massive bodies (masses replace charges in equation 1.5). We can derive classical orbits (analogous to those of planets orbiting the sun) by equating this electrostatic force, Fe, with the centripetal force, Fc, due to an electron’s circular motion around the nucleus:
Electromagnetic waves and wave-particle duality
Energy, in the form light, heat or sound, may be transmitted from place to place by waves. These may be either transverse (as in the case of electromagnetic waves transporting light and heat) or longitudinal (sound waves). Electromagnetic waves are composed of oscillating transverse electric and magnetic fields, illustrated in Figure 1.1. In transverse waves, the direction of oscillation is normal to the direction of propagation, whereas longitudinal waves contain oscillations in the direction of propagation in the form of compressions and rarefactions. For radiotherapy applications, we are mostly concerned with the very high frequency end of the electromagnetic spectrum, shown in Figure 1.2. We can consider an x-ray photon to behave either as a particle or a wave, expressing wave-particle duality. The frequency, in cycles per second or Hertz (Hz), ν of the radiation relates to its energy per particle, or quantum, through:

Figure 1.2 The electromagnetic spectrum. Approximate energy ranges are indicated on the left in electron-volts (1 eV = 1.602×10−19 J) and wavelengths on the right (adapted from [2]). (1 GeV = 1×109 eV, 1 μm = 1×10−6 m, 1 nm = 1×10−9 m, 1 fm = 1×10−15 m).
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


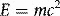 1.1
1.1 1.2
1.2 1.3
1.3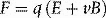 1.4
1.4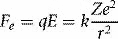 1.5
1.5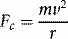 1.6
1.6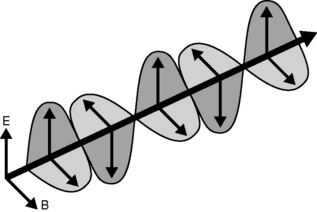
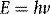 1.7
1.7