Basic Principles of MRI
Introduction
In this chapter, we will discuss the basic principles behind the physics of magnetic resonance imaging (MRI). Some of these principles are explained using Newtonian physics, and some using quantum mechanics, whichever can convey the message more clearly. Although this might be confusing at times, it seems to be unavoidable. In any case, we’ll try to keep it straightforward.
Nuclear magnetic resonance (NMR) is a chemical analytical technique that has been used for over 50 years. It is the basis for the imaging technique we now call MRI. (The word nuclear had the false connotation of the use of nuclear material; thus, it was discarded from the MR lexicon, and “NMR tomography” was replaced by the phrase magnetic resonance imaging [MRI].)
Table 2-1 The Electromagnetic Spectrum Illustrating the Windows for Radio waves, Microwaves, Visible Light, and X-Rays | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Electromagnetic Waves
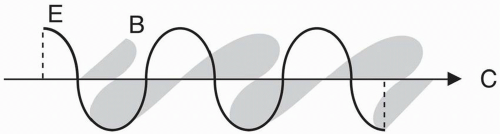
To understand MRI, we first need to understand what an electromagnetic wave is. Table 2-1 demonstrates the characteristics of a variety of electromagnetic waves, including X-ray, visible light, microwaves, and radio waves. All electromagnetic waves have certain fundamental properties in common:
They all travel at the speed of light c = 3 × 108 m/sec in a vacuum.
By Maxwell’s wave theory, they all have two components—an electric field E and
a magnetic field B—that are perpendicular to each other (Fig. 2-1). We will designate the sinusoidal wave, which is drawn in the plane of the paper, the electrical field E. Perpendicular to it is another sinusoidal wave, the magnetic field B. They are perpendicular to each other and both are traveling at the speed of light (c). The electric and magnetic fields have the same frequency and are 90° out of phase with each other. (This is because the change in the electric field generates the magnetic field, and the change in the magnetic field generates the electric field. For this reason, electromagnetic waves are self-propagating once started and continue out to infinity.)
Figure 2-1. Two components of an electromagnetic wave, the electric component E and the magnetic component B. These two components are perpendicular to each other, are 90° out of phase, and travel at the speed of light (c).
If we think in terms of vectors, the vectors B and E are perpendicular to each other, and the propagation factor C is perpendicular to both (Fig. 2-2). Both the electrical and magnetic components have the same frequency ω. So what we get is a vector that is spinning (oscillating) around a point at angular frequency ω. Remember, the angular frequency ω is related to the linear frequency f:
ω = 2πf
We are interested in the magnetic field component—the electric field component is undesirable because it generates heat.
 Figure 2-2. The vector representation of B, E, and C. |
Table 2-2 | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Table 2-3 | ||||||||
|---|---|---|---|---|---|---|---|---|
|
Table 2-2 summarizes the important electromagnetic windows in nature. In this table, the following notations are used:
keV = 103 eV = kilo-electron-volts
pm = 10-12 m = picometer
nm = 10-9 m = nanometer
MeV = 10-3 eV = million electron volts
In MRI, we deal with much lower energies than X-ray or even visible light. We also deal with much lower frequencies. (The energy of an electromagnetic wave is directly proportional to its frequency, E = hv.) The wave lengths are also much longer in the radio frequency (RF) window. Table 2-3 contains a few examples of frequency ranges in the electromagnetic spectrum.
 Figure 2-3. A spinning charged particle generates a magnetic field. |
Spins and Electromagnetic Field
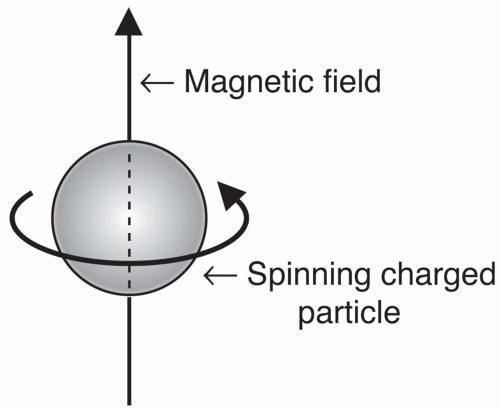
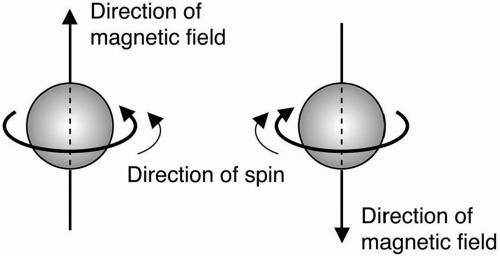
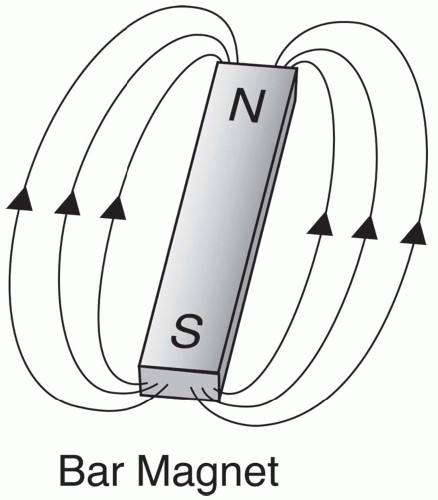
One of the pioneers of NMR theory was Felix Bloch of Stanford University, who won the Nobel Prize in 1946 for his theories. He theorized that any spinning charged particle (like the hydrogen nucleus) creates an electromagnetic field (Fig. 2-3). The magnetic component of this field causes certain nuclei to act like a bar magnet, that is, a magnetic field emanating from the south pole to the north pole (Fig. 2-4).
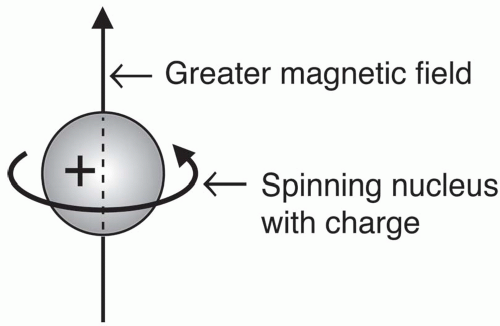
In MRI, we are interested in charged nuclei, like the hydrogen nucleus, which is a single, positively charged proton (Fig. 2-5).
In MRI, we are interested in charged nuclei, like the hydrogen nucleus, which is a single, positively charged proton (Fig. 2-5).
 Figure 2-4. A bar magnet with its associated magnetic field. |
 Figure 2-5. A spinning charged hydrogen nucleus (i.e., a proton) generating a magnetic field. |
The other thing that we know from quantum theory is that atomic nuclei each have specific energy levels related to a property called spin quantum number S. For example, the hydrogen nucleus (a single proton) has a spin quantum number S of 1/2:
S (1H) = 1/2
The number of energy states of a nucleus is determined by the formula:
Number of energy states = 2S + 1
For a proton with a spin S = 1/2, we have
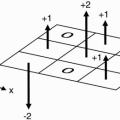
Number of energy states = 2 (1/2) + 1 = 1 + 1 = 2 Therefore, a hydrogen proton has two energy states denoted as − 1/2 and + 1/2. This means that the hydrogen protons are spinning about their axis and creating a magnetic field. Some hydrogen protons spin the opposite way and have a magnetic field in just the opposite direction. The pictorial representation of the direction of proton spins in Figure 2-6 represents the two energy states of the hydrogen proton. Each one of these directions of spin has a different energy state.
 Figure 2-6. The direction of the generated magnetic field depends on the direction of rotation of the spinning protons. |
Other nuclei have different numbers of energy states. For example, 13Na has a spin S = 3/2
Number of energy states of 13Na = 2 (3/2) + 1 = 4
The four energy states of 13Na are denoted as (−3/2, −1/2, 1/2, 3/2).
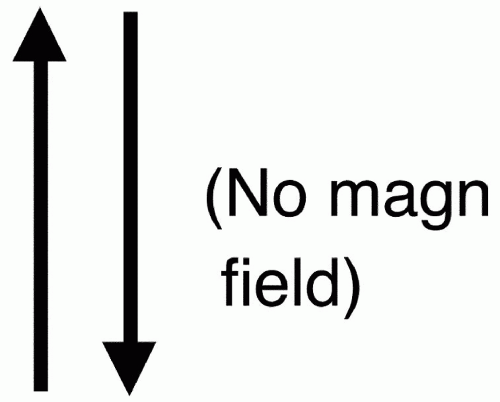
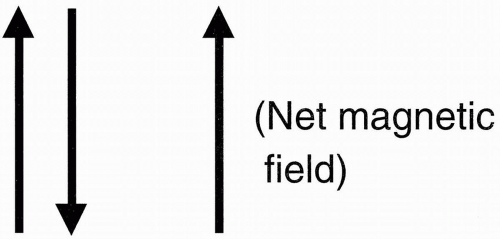
The important fact about all this is that in the hydrogen proton, we have one proton with two energy states that are aligned in opposite directions, one pointing north (parallel), and the other pointing south (antiparallel). (If there were an even number of protons in the nucleus, then every proton would be paired: for every proton spin with magnetic field pointing up, we’d have a paired proton spin with magnetic field pointing down (Fig. 2-7). The magnetic fields of these paired protons would then cancel each other out, and the net magnetic field would be zero.) When there are an odd number of protons, then there always
exists one proton that is unpaired. That proton is pointing either north or south and gives a net magnetic field (Fig. 2-8) or a magnetic dipole moment (MDM) to the nucleus. Actually, an MDM is found in any nucleus with an odd number of protons, neutrons, or both. Dipole-dipole interactions refer to interactions between two protons or between a proton and an electron.
exists one proton that is unpaired. That proton is pointing either north or south and gives a net magnetic field (Fig. 2-8) or a magnetic dipole moment (MDM) to the nucleus. Actually, an MDM is found in any nucleus with an odd number of protons, neutrons, or both. Dipole-dipole interactions refer to interactions between two protons or between a proton and an electron.
 Figure 2-7. The magnetic fields of paired protons (rotating in opposite directions) cancel each other out, leaving no net magnetic field. |
The nuclei of certain elements, such as hydrogen (1H) and fluorine (19F), have these properties (Table 2-4). Every one of these nuclei with an odd number of protons or neutrons can be used for imaging in MR. However, there is a reason why we stay with hydrogen. We use hydrogen for imaging because of its abundance. Approximately 60% of the body is water. We find hydrogen protons (1H), for example, in water (H2O) and fat (—CH2—). Later on we’ll find out how we use the spin of the hydrogen proton and avoid the spins of all the other nuclei with odd numbers of protons.
 Figure 2-8. Unpaired protons yield a net magnetic field. |
Magnetic Susceptibility
All substances get magnetized to a degree when placed in a magnetic field. However, the degree of magnetization varies. The magnetic susceptibility of a substance (denoted by the Greek symbol χ) is a measure of how magnetized they get. In other words, χ is the measure of magnetizability of a substance.
To develop a mathematical relationship between the applied and induced magnetic fields, we first need to address the confusing issue regarding the differences between the two symbols encountered when dealing with magnetic fields: B and H. We caution the reader that the following discussion is merely a simplification; an advanced physics textbook will have details on the theory of electromagnetism. The field B is referred to as the magnetic induction field or magnetic flux density, which is the net magnetic field effect caused by an external magnetic field. The field H is referred to as the magnetic field intensity. These two magnetic fields are related by the following:
B = µH or µ = B/H
where µ represents the magnetic permeability, which is the ability of a substance to concentrate magnetic fields. The magnetic susceptibility χ is defined as the ratio of the induced magnetic field (M) to the applied magnetic field H:
M = χH or χ = M/H
Furthermore, χ and µ are related by the following:
µ = 1 + χ
making sure that the units used are consistent.
Three types of substances—each with a different magnetic susceptibility—are commonly dealt with in MRI: paramagnetic, diamagnetic, and ferromagnetic. These are described below.
Paramagnetism, Diamagnetism, and Ferromagnetism.
Diamagnetic substances have no unpaired orbital electrons. When such a substance is placed in an external magnetic field B0, a weak magnetic field (M) is induced in the opposite direction to B0. As a result, the effective magnetic field is reduced. Thus, diamagnetic substances have a small, negative magnetic susceptibility χ (i.e., χ < 0 and µ < 1). They are basically nonmagnetic. The vast majority of tissues in the body have this property. An example of diamagnetic effect is the distortion that occurs at an air-tissue interface (such as around paranasal sinuses).
Paramagnetic substances have unpaired orbital electrons. They become magnetized while the external magnetic field B0 is on and become demagnetized once the field has been turned off. Their induced magnetic field (M) is in the same direction as the external magnetic field. Consequently, their presence causes an increase in the effective magnetic field. They, therefore, have a small positive χ (i.e., χ > 0 and µ > 1) and are weakly attracted by the external magnetic field. In such substances, dipole-dipole (i.e., proton-proton and proton-electron) interactions cause T1 shortening (bright signal on T1-weighted images). The element in the periodic table with the greatest number of unpaired electrons is the rare earth element gadolinium (Gd) with seven unpaired electrons, which is a strong paramagnetic substance. Gd is a member of the lanthanide group in the periodic table. The rare earth element dysprosium (Dy) is another strong paramagnetic substance that belongs to this group. Certain breakdown products of hemoglobin are paramagnetic: deoxyhemoglobin has four unpaired electrons, and methemoglobin has five. Hemosiderin, the end stage of hemorrhage, contains, in comparison, more than 10,000 unpaired electrons. Hemosiderin belongs to a group of substances referred to as superparamagnetic, which have magnetic susceptibilities 100 to 1000 times stronger than paramagnetic substances.Related posts:
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
