Pulse Sequences Part II (Spin Echo)

Introduction

This chapter focuses on the most frequently used pulse sequence—the spin echo (SE) pulse sequence. When the concept of dephasing was discussed in previous chapters, we brought up two main causes: (i) external magnetic inhomogeneity, and (ii) inherent spin-spin interactions. The SE pulse sequence eliminates the former by an additional refocusing or rephasing 180° radio frequency (RF) pulse. By using the SE pulse sequence, we can eliminate dephasing caused by fixed external magnetic field inhomogeneities. (We can’t eliminate spin-spin interactions because they are not fixed, i.e., they fluctuate randomly.)

Spin-Echo Pulse Diagram

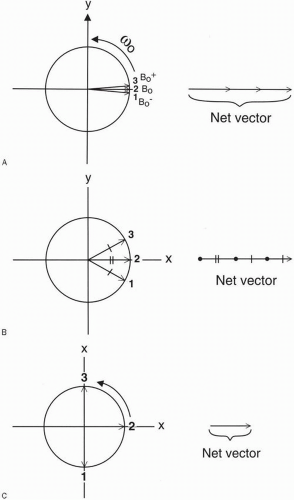
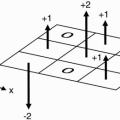
As a result of the 90° pulse, the magnetization vector M_z is flipped into the x-y plane. Consider the precession of three different magnetization vectors in the transverse plane, each in a slightly different magnetic environment (Fig. 8-1A). Initially, all these vectors are in phase and they are all precessing at frequency ω₀.

In Figure 8-1A, say one group of spins is exposed to the magnetic field B₀, which causes them to precess at frequency ω₀. The adjacent group of spins sees a slightly higher field B₀ ⁺ and precesses at a slightly higher frequency ω₀ ⁺, and another sees a slightly lower field B₀ ⁻ with a precessional frequency of ω₀⁻. After the 90° pulse, the three spins will begin to get out of phase with each other (Fig. 8-1B). Eventually, the fast vector and the slow vector become 180° out of phase and cancel each other out (Fig. 8-1C).

Analogy

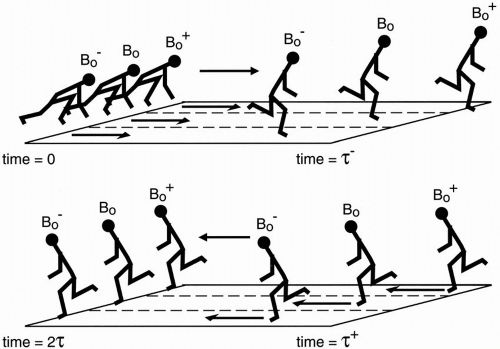
Let’s consider the analogy of three runners running around the track (Fig. 8-2). Initially, they start out at the same point. After they run for a time τ, they are no longer together—one is running faster and gets ahead of the others, and one is running slower, falling behind the others.

At this time, if we make the runners turn around and run the opposite way, each one will still be running at the same speed (precessing at the same frequency in the case of the spins). They have just changed direction and are running back to where they started. Each one will then run the same distance if they run the same amount of time τ. Therefore, at time 2τ, they will all come back at the starting point at the same time and will be back together in phase. The action of making the runners change direction is done with the use of a 180° refocusing pulse in the case of the spins.

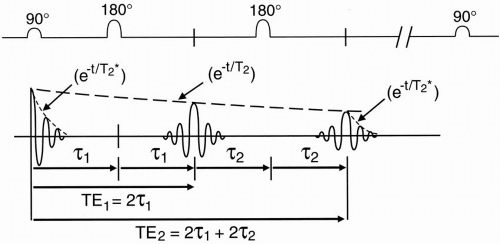
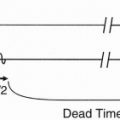
Thus, at a certain time τ after the 90° pulse, when the spins have gotten out of phase, a 180° pulse is applied. Now all the spins flip 180° in the x-y plane and they continue precessing, but now in the opposite direction (Fig. 8-3). Let’s look at the pulse sequence diagram (Fig. 8-4). We start off with a 90° RF pulse to flip the spins into the x-y plane. We wait a time τ and apply a 180° RF pulse. Then we wait a long time, TR, and repeat the process.

If we draw the free induction decay (FID) after the 90δ pulse, we see that the FID dephases

very rapidly due to the T2^* effect related to external magnetic field inhomogeneities and spin-spin interactions. The spins get out of phase. After time τ we apply the 180δ refocusing pulse. After an equal time τ they will be completely in phase again, and the signal will reach a maximum.

Figure 8-1. Three magnetization vectors in three slightly magnetic environments. In (A) they are in phase and their vector sum is three times each individual vector. In (B) they are slightly out of phase, yielding a smaller net vector. In (C) vector 1 and 3 cancel each other out because they are 180δ out of phase, leaving only vector 2.

Figure 8-2. Analogy of three runners on a track. At time τthey are made to turn around and run back toward the starting point. Because the slowest runner is now in the lead, they will all reach the starting point at exactly the same time (at time 2τ).

Time τ is the time from the 90° RF pulse to the 180° RF pulse.
Time τ is also the time from the 180° RF pulse to the point of maximum rephasing, that is, the echo.
We call 2τ the echo delay time (time to echo)—TE: the time after the 90° pulse when we get maximum signal again.
The 180° pulse is, therefore, called a refocusing or rephasing pulse.

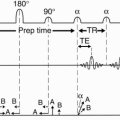
We can apply a second 180° pulse. Now, instead of one 180° pulse following the 90° pulse, we have two 180° pulses in sequence after a 90° pulse (Fig. 8-5). After the first echo, the spins will begin to dephase again. A second 180° pulse applied at time τ₂ after the first echo will allow the spins to rephase again at time 2τ₂ after the first echo and a second echo is obtained. Each echo has its own TE.

The time from the 90° pulse to the first echo is TE₁.
The time from the 90° pulse to the second echo is TE₂.

Ideally, we would like to regain all the signal from the original FID. In practice, it can’t happen. We are able to regain the signal lost due to fixed external magnetic field inhomogeneities by applying a refocusing 180° pulse, but dephasing caused by spin-spin interaction of the tissue cannot be regained. If we join the points of maximum signal due to rephasing as a result of the 180° pulses, we will get an exponentially decaying curve with a time constant given by T2. Therefore, the decay of the original FID and the decay of each subsequent echo is given by e^−t/^T2*, whereas the decay of the

curve describing the maximum signal reached by each echo is given by e^−t/^T2. This is the difference between T2^* and T2.

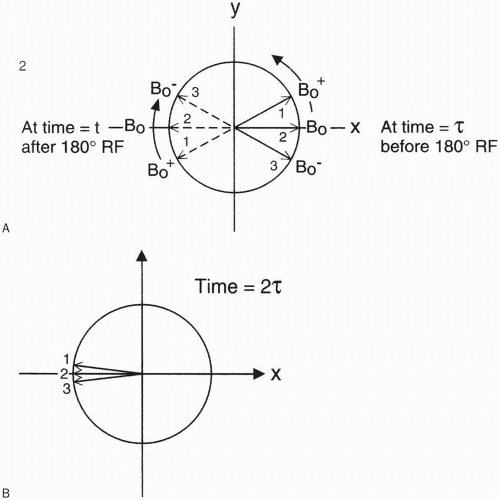Figure 8-3. The vectors in Figure 8-1 are reversed 180° in direction at time τ (A), so that at time 2τ they’ll get in phase again (B).

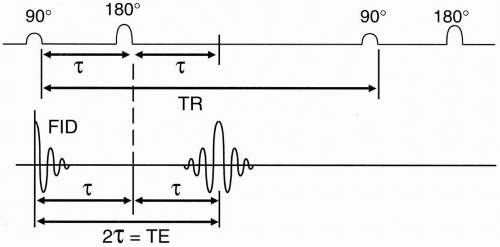Figure 8-4. In a spin-echo pulse sequence, a 180° pulse is applied at time τ, causing the spins to get in phase at time 2τ. This leads to the formation of an echo from the FID.