Basic Radiation Physics

Fig. 1.1

Electric and magnetic field propagated as a transverse wave perpendicular to each other and perpendicular to the direction of propagation

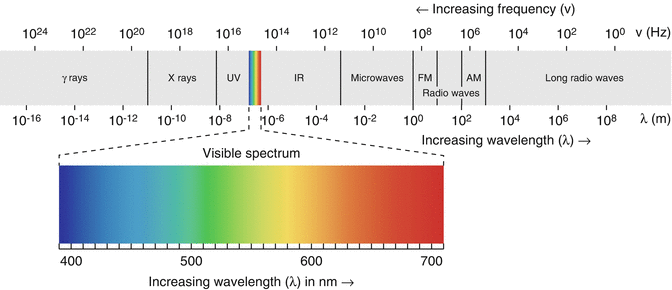
Fig. 1.2

Electromagnetic spectrum: Waves with shorter wavelength will have high frequency and vice versa. Ionizing radiation with high frequency is more energetic and can induce biological effects

1.2.1 Wave/Particulate Nature of Radiation

Although wave and particle having different physical characteristics, electromagnetic radiation can behave as both at once (wave-like and particle-like). Many experiments showed that radiation is sometimes behaves as wave and sometimes behaves as particle concluding that wave and particle cannot be separated, only together the phenomena can be explained. This has been proposed by a number of scientists leading to the theory of wave – particle duality.

1.2.2 Duality Principle

The duality principle describes the elementary particles and electromagnetic radiation in terms of wave and particle-like characteristics. It was not originated from a single scientist or revealed from only one experiment. Max Plank has stated that energy is transferred in a form of packets or quanta, while Albert Einstein thought of light as particle-like or localized in packets of discrete energy in contrast to its original definition as wave-like properties. Another contribution came from the phenomenon of photoelectric effect proposed also by Einstein. He stated that the emission of photoelectrons from metal plates does occur if and only if the incident photons on photoemissive plate have a threshold wavelength of energy that is able to liberate electrons from the metal. Then, Louis de Broglie proposed that electrons and other particles can behave as waves and has wavelength and frequencies. While this proposal was in 1927, the announcement of the understanding of the wave and particle aspects of matter was carried out in 1928. See Fig. 1.3.

Fig. 1.3

Duality principle: Particles and electromagnetic radiation possess waves and particle characteristics (From http://www.lab-initio.com/quantum.html)

Radiation can be described in terms of packet of energy, called photons. The energy of a photon is given by

$E\kern0.5em \left(\mathrm{photon}\right)\kern0.5em =\kern0.5em hv\kern0.5em =hc/l$

(1.1)

where h is plank’s constant (h = 6.625 6 × 10⁻³⁴ J s); $\nu$ and λ are characteristics frequency and wavelength, respectively; and c is the speed of light in vacuum (Table 1.2).

Waves are characterized by frequency, wavelength and phase. Electromagnetic radiation is massless with no charge, while wavelength and frequency of oscillating fields are related to each other by the following equation:

$c=\kern0.5em \lambda v$

(1.2)

However, they are still affected by gravity.

It is of relevance to mention here that many diagnostic imaging modalities rely heavily on physical properties of different electromagnetic radiations. For example, in x-ray computed tomography (CT), a uniform x-ray beam interacts with the human tissues, and the transmitted amount is measured by the CT detector to reveal an image that reflects the attenuation properties of the tissue covered in the scanning beam. Radiologic techniques such as fluoroscopy, angiography and x-ray radiography are also dependent on x-ray radiations in eliciting important diagnostic information for a wide range of human diseases and abnormalities.

Electromagnetic radiation is also associated with nuclear medicine in the sense that gamma emission is used in many diagnostic purposes utilizing the powerful penetrating capabilities of the radiation beam. This essentially takes place when patient is injected with pharmaceutical compound labelled to gamma-emitting radionuclide. After radiopharmaceutical administration, the body tissue will be the source of gamma ray emission that is used in the imaging process.

Another application of electromagnetic radiation in clinical practice is magnetic resonance (MR) imaging which is different from other imaging techniques such as CT and nuclear medicine, as it uses radio frequency (i.e. radio wave) as energy source rather than ionizing radiation. The procedure requires the usage of a strong magnetic field for spin alignment of hydrogen nuclei in the body. The spin synchronizes as the radio-frequency pulse matches the nuclear resonance frequency of the protons.

While radio wave energy is consistent with energy of nuclear spin in magnetic field, microwave matches rotational energy of the molecule. The infrared (IR) region in the spectrum lies beyond the region that the human eye perceives as red light. The absorption of infrared light causes increases in the frequencies at which the bonds between atoms stretch and bend. This is the idea behind infrared spectroscopy where there is a sort of matching between the IR radiation energy and the frequency of a specific molecular motion usually bond bending or stretching. However, the higher-frequency ultraviolet radiation that lies above the visible limit of the light spectrum is matching to different electronic transition states. In summary:

Radio → nuclear spin in magnetic field
Microwave → rotation
Infrared → vibration
Ultraviolet → electronic

1.3 Atomic Models

Atom is considered as the basic building unit of an element. An atom is the smallest unit of element that retains its physical and chemical properties. Each known element has atoms differ from the atoms of other elements; this gives each element a unique atomic structure. Many atomic models were proposed, and some have been adopted as ways to describe the atom. Neither of them is perfect, but they have relative contributions towards understanding these building blocks. See Figure 1.4 serial time line of atomic models.

Fig. 1.4

Serial time line of atomic models proposed over the years and described by the following scientists (left to right): Democritus, Dalton, Thomson, Rutherford and Bohr. Taken from http://www.K12tlc.net/content/atomhist.htm

1.3.1 History of Atomic Models

The first atomic model described in the literature is dated back to the Greek philosopher Democritus. He postulated the existence of invisible atoms, which are characterized only by quantitative properties such as size, shape and motion. His model described the atom as indivisible spheres representing the smallest piece of an element that still behave like the entire chunk of matter. There were no significant advances in definition and characterization of the atom until the English chemist John Dalton started to look at this in the 1800s. Dalton shared the same thoughts and impression as Democritus about atom in the sense that it is tiny and indivisible particles, but he introduced new assumptions about atom. The main assumptions of Dalton model were:

All matter was composed of atoms, indivisible and indestructible. While all atoms of an element are identical and have the same properties, different elements have atoms of different size and mass.
All compounds are composed of combinations of these atoms in defined ratios.
Atoms can combine to form different compounds (e.g. carbon and oxygen combine to form carbon monoxide CO and carbon dioxide CO₂).
Chemical reactions resulted in rearrangement of the reacting atoms.

In 1897, J.J. Thomson discovered the electron in series of experiments designed to study the nature of electric discharge in a high-vacuum cathode ray tube. In 1904, Thomson introduced a new atom model that differs from pervious atom models suggesting that the atom is uniform sphere of positively charged matter in which electrons are positioned by electrostatic forces.

A monumental breakthrough came in 1911 based on experimental results when Ernest Rutherford and his colleagues Hans Geiger and Ernest Marsden conducted the famous gold foil experiment intended to determine angles through which a beam of alpha particles (helium nuclei) would scatter after passing through a thin foil of gold. It was a new but exciting moment when they found few alpha particles recoiled almost directly backwards. It was Rutherford’s interpretation that this happen when a positively charged and relatively heavy target particle, such as the proposed nucleus, could account for such strong repulsion. The negative electrons that balanced electrically the positive nuclear charge were regarded as travelling in circular orbits around the nucleus (Fig. 1.5) like planets that move around the stars, and therefore this model was called planetary model.

Fig. 1.5

Planetary model: In this model Rutherford proposed that electrons move in circular path around a central positive mass. This was contradicted by the fact that revolution makes electron lose energy while moving in spiral path and fall into the positively charged nucleus under influence of attraction force

The planetary model was greatly inconsistent with Thomson’s hypothesis in which the atom is a mixture of positive and negative particles that uniformly mixed throughout the atom. Based on the classical electromagnetic theory, however, the model failed to solve stability problem of the atom as the electrons lose energy and falling into the nucleus under the influence of attraction forces. The model proposed by Rutherford relied heavily on classical physics and was superseded in a few years by the Bohr atomic model, which incorporated some early quantum theory in combination with some classical concepts.

1.3.2 Bohr Model

In 1913, Bohr introduced a new model to explain atom stability. Bohr model of the atom was the first model that incorporated quantum theory and was the predecessor of wholly quantum-mechanical models. The model focused on electron description and based on spectroscopic observations. Bohr built up his model with the following postulates:

The electron exists in certain energy levels (stationary states) with circular movement around the nucleus.
Transition between these stationary states is accompanied with emission or absorption of electromagnetic radiation. The energy difference between these two energy levels is given by

$\varDelta E\kern0.5em =\kern0.5em \hslash v$

(1.3)
where ħ (i.e. h bar) or sometimes reduced plank’s constant is commonly associated with angular momentum and given by

$\hslash \kern0.5em =\kern0.5em h/2\pi$

(1.4)
Quantization of orbit. The only allowed orbits (stationary states) are those for which the angular momentum L is

$L\kern0.5em =\kern0.5em n\hslash$

where n is principal quantum number and takes values of 1,2,3,….., n and cannot be less than one.

Bohr’s postulates were experimentally confirmed in experiments of Franck and Hertz (German scientists) in 1913 who studied the inelastic scattering of electrons of mercury atoms. This experiment showed that the energy levels of mercury atom were discrete. However, Bohr’s model had no way of approaching non-periodic quantum-mechanical phenomena, like scattering. Furthermore, although Bohr’ model served to predict energy levels, it was not able to explain transition rates between levels. Finally, the model was successful only for one-electron atoms like hydrogen and fails even for helium. To correct these drawbacks, one needs to apply a more completely quantum-mechanical treatment of atomic structure, and such an approach is used in Schrödinger theory.

1.3.3 Quantum Mechanics Model

The quantum mechanics model is derived from the quantum theory in which electron location and momentum are governed by the wave function. This hypothesis is denoted as uncertainty principle (Heisenberg principle) and states that the position and momentum of the electron can’t be determined simultaneously with the same high precision. Stated another way, the more the precision in determining the electron location, the low the probability of determining the momentum and vice versa. The theory used the term orbitals to describe the location of the electrons, which are volumes in space used to define the probability distribution function. Four quantum numbers were introduced to define the electrons and their orbitals around the nucleus:

1.

Principle quantum number (n): it is an integer number that indicates electron energy and orbital size, and it is the same number introduced by Bohr. It takes values n = 0,1,2,……, while the maximum number of electrons in certain energy level is equal to 2n ².
2.

Angular quantum number (l) describes the orbital shape of a particular principal quantum number. It divides energy shells or levels into subshells (sublevels). These sublevels represented by letters like s, p, d and f. Angular quantum number takes values l = 0,1,2…,n−1.
3.

Magnetic quantum number, m _l (m _l = −l,…, 0,…, +l) specifies the orientation in space of an orbital of a given energy (n) and shape (l). This number divides the subshell into individual orbitals which hold the electrons; there are 2l+1 orbitals in each subshell.
4.

Spin quantum number, m _s (m _s = +½ or −½) defines the orientation of the spin axis of an electron. An electron can spin in only one of two directions.

1.4 Structure of the Atom

As mentioned earlier, an atom is the main building block of matter. The atomic mass is concentrated in the nucleus which considered the heaviest portion of the atom. The positively charged nucleus contains particles of nearly equal mass, protons and neutrons, electrically balanced with negatively charged electrons moving in certain orbitals around it. Any element can be represented as

$\begin{array}{c}A\\ {}Z\end{array}X$

where A atomic mass number is the sum of protons number Z and neutrons number N. The atomic number Z equals also the number of electrons in stable nuclei. It is not applicable to have two different elements having the same atomic number. The periodic table is arranged by order of increasing atomic number, which is always an integer. On the other hand, different forms of the same element can have different masses (i.e. have same atomic number) which are called isotopes, while those that have the same number of neutrons are called isotones. Isobars are nuclide with different numbers of protons and neutrons but with the same mass number. Examples of the three different nomenclatures are described in Table 1.1.

Table 1.1

Some examples of isotopes, isobars and isotones

Isotopes	Same Z	₈¹⁶O	₈¹⁷O	₈¹⁸O
		Z = 8
Isobars	Same A	₉¹⁸F		₈¹⁸O
		A = 18
Isotones	Same N	₉¹⁹O		₈¹⁸O
		N = 10

1.4.1 Mass and Energy

Mass and energy were considered two different quantities. Early 1900s, Einstein proved by his equation that neither mass nor energy was conserved separately. Thus, the mass can be converted to energy and vice versa while total mass- energy was conserved. In the following section the conversion of mass and energy will be demonstrated.

1.4.2 Atomic Mass Unit

The first atomic weight was initially proposed by John Dalton in 1803 as the mass of the hydrogen atom, H-1. Then it was suggested by Wilhelm Ostwald that it can best expressed in terms in units of 1/16 of the weight of the oxygen atom. Atomic mass can be measured by approximating the weight of a proton or neutron which indicates the masses of atom nucleons. The atom mass is expressed by a unified unit called the atomic mass unit denoted by the symbol u. In 1961, the international union of pure and applied chemistry had adopted and defined the modern applications of atomic mass unit and related it to the mass of carbon-12.

The definition of the atomic masses has been based on the unified mass scale considering one mole of carbon-12 which by conversion equals 12 g as the best reference nuclide. Determination of ¹²C atom mass in grams using Avogadro’s number divided on the total number of the individual atom nucleons indicates the masses of these nucleons which used to convert one atomic mass unit (1 u) to grams. Therefore, the atomic mass unit is one-twelfth ¹²C atom in its electronic and nuclear ground state:

$1\kern0.5em \mathrm{u}=\frac{1}{12}m\left({}_6{}^{12}\mathrm{C}\right)$

$\begin{array}{rcl}\mathrm{Thus},\ \mathrm{mass}\ \mathrm{ofone}\ \mathrm{atom}\ {\mathrm{of}}^{12}\mathrm{C}& =& \frac{12\mathrm{g}/\mathrm{mol}}{6.022\kern0.5em 141\kern0.5em 29\times {10}^{23}\mathrm{atom}\mathrm{s}/\mathrm{mol}}\\ {}& =& 1.992\kern0.5em 646\kern0.5em 705\times {10}^{-23}\mathrm{g}/\mathrm{atom}\end{array}$

$\begin{array}{rcl}\mathrm{The}\ \mathrm{mass}\ \mathrm{per}\ \mathrm{nucleon}& =& \frac{1.992\kern0.5em 646\kern0.5em 705\times {10}^{-23}\mathrm{g}/\mathrm{atom}}{12}\\ {}& =& 1.660\kern0.5em 538\kern0.5em 921\times {10}^{-24}\mathrm{g}\end{array}$

Then, 1 u = 1.660 538 921 × 10⁻²⁷ kg.

Now the mass of proton and neutron in terms of atomic mass unit can be determined by using its actual mass in grams:

$\begin{array}{rcl}\mathrm{Proton}\ \mathrm{mass}\ \left({m}_{\mathrm{p}}\right)& =& \frac{1.672\kern0.5em 621\kern0.5em 777\times {10}^{-27}}{1.660\kern0.5em 538\kern0.5em 921\times {10}^{-27}}=1.007\kern0.5em 276\kern0.5em 467\kern0.5em \mathrm{u}\\ {}\mathrm{Neutron}\ \mathrm{mass}\ \left({m}_{\mathrm{n}}\right)& =& \frac{1.674\kern0.5em 927\kern0.5em 351\times {10}^{-27}}{1.660\kern0.5em 538\kern0.5em 921\times {10}^{-27}}=1.008\kern0.5em 664\kern0.5em 916\kern0.5em \mathrm{u}\end{array}$

Conversion of the energy unit from the SI scale to the unified atomic mass unit is being done by using Einstein’s mass-energy relationship (E = mc ² where c is the speed of light in vacuum) taking into account that 1 eV = 1.602 176 565 × 10⁻¹⁹ kg.m²/s. Inserting this quantity of mass 1 u = 1.660 538 921 × 10⁻²⁷ into Einstein’s equation and applying conversion factors, the nucleons mass equivalent energy can be determined.

$E=m{c}^2$

(1.4)

$\begin{array}{l}=1\kern0.5em \mathrm{u}\left(\frac{1.660\kern0.5em 538\kern0.5em 921\times {10}^{-27}\mathrm{kg}}{\mathrm{u}}\right)\times {\left(299\kern0.5em 792\kern0.5em 458\kern0.5em \mathrm{m}/\mathrm{s}\right)}^2\left(\frac{1\kern0.5em \mathrm{N}}{1\kern0.5em \mathrm{kg}.\frac{\mathrm{m}}{{\mathrm{s}}^2}}\right)\left(\frac{1\kern0.5em \mathrm{J}}{N.m}\right)\hfill \\ {}=1.492\kern0.5em 417\kern0.5em 955\times {10}^{-10}\mathrm{J}\left(\frac{1\kern0.5em \mathrm{M}\mathrm{e}\mathrm{V}}{1.602\kern0.5em 176\kern0.5em 565\times {10}^{-13}\mathrm{J}}\right)\hfill \\ {}=931.494\kern0.5em 060\kern0.5em 9\kern0.5em \mathrm{M}\mathrm{e}\mathrm{V}\hfill \end{array}$

Some of the constants and conversion factors used in the above derivations can be found in Table 1.2 which provides a number of useful physical quantities and constants used in converting mass into energy and vice versa.

Table 1.2

Summary of several physical quantities and constants in atomic and nuclear scale used in mass-energy conversion

Quantity	Symbol	Numerical value	Unit
Avogadro’s number	N _A	6.022 141 29 × 10²³	mol⁻¹
Speed of light in vacuum	C	299 792 458	m/s
Electron volt	eV	1.602 176 565 × 10⁻¹⁹	J
Atomic mass unit-kilogram relationship	1 u	1.660 538 921 × 10⁻²⁷	kg
Atomic mass unit-electron volt relationship	1 u (C²)	931.494 061 × 10⁶	eV
Atomic mass unit-joule relationship	1 u (C²)	1.492 417 954 × 10⁻¹⁰	J
electron Volt-atomic mass unit relationship	1 eV/C²	1.073 544 150 × 10⁻⁹	u
Electron mass Energy equivalent	m _e	9.109 382 91 × 10⁻³¹	kg
	m _e	5.485 799 094 6 × 10⁻⁴	u
	m _eC²	8.187 105 06 × 10⁻¹⁴	J
	m _eC²	0.510 998 928	MeV
Proton mass Energy equivalent	m _p	1.672 621 777 × 10⁻²⁷	kg
	m _p	1.007 276 466 812	u
	m _pC²	1.503 277 484 × 10⁻¹⁰	J
	m _pC²	938.272 046	MeV
Neutron mass Energy equivalent	m _n	1.674 927 351 × 10⁻²⁷	kg
	m _n	1.008 664 916 00	u
	m _nC²	1.505 349 631 × 10⁻¹⁰	J
	m _nC²	939.565 379	MeV

Source: NIST (2010 CODATA recommended values)

1.4.3 Binding Energy and Mass Defect

For all nuclei, the mass of the nucleus that have been formed is always less than the total composed masses of the contributing nucleons. This is due to conversion of that mass difference to the required energy for holding these nucleons together (i.e. the conversion of mass to binding energy). This mass difference is known as the mass defect and represents the binding energy which is defined as the amount of energy that need to be supplied to a nucleus to completely separate its constituent nucleons. The mass defect can be calculated by adding up the masses of the constituent particles and then subtracting the known mass of that atom:

$\begin{array}{l}\varDelta\ m=\left[Z\left({m}_{\mathrm{proton}}+{m}_{\mathrm{electron}}\right)+\left(A-Z\right){m}_{\mathrm{neutron}}\right]\\ {}\kern3.25em -{m}_{\mathrm{atom}}\end{array}$

(1.5)

where:

Δm = mass defect (u)

m _proton = mass of a proton

m _electron = mass of electron

m _neutron = mass of neutron

m _atom = mass of the nuclide

Z is the atomic number and A is the mass number.

Since 1 u is equivalent to 931.5 MeV of energy as calculated in Sect. 1.4.2, the binding energy can be calculated by

$\mathrm{B}.\mathrm{E}.\kern0.5em =\kern0.5em \varDelta\ m\left(\frac{931.5\kern0.5em \mathrm{M}\mathrm{e}\mathrm{V}}{1\kern0.5em \mathrm{u}}\right)$

Example

Calculate the mass defect of ²³⁵U provided that the mass of the atom is 235.043 9 u?

Solution:

The atomic number of the ²³⁵U is 92. The mass defect can be calculated by using Eq. 1.5.

$\begin{array}{c}\varDelta\ m=\left[Z\left({m}_{\mathrm{proton}}+{m}_{\mathrm{electron}}\right)+\left(A-Z\right){m}_{\mathrm{neutron}}\right]-{m}_{\mathrm{atom}}\\ {}\varDelta\ m=\left[92\left(1.007\kern0.5em 28+5.485\kern0.5em 79 \times {10}^{-4}\right)+\left(235-92\right)1.008\kern0.5em 66\right]-235.043\kern0.5em 9\\ {}=1.914\kern0.5em 71\ \mathrm{u}\end{array}$

1.4.4 Nuclear Stability

Since Earth formation, there were about 275 stable nuclides found in nature, and more than 2000 nuclides are known to be unstable (i.e. radioactive). The constituents of the unstable nuclei are not arrayed in the lowest potential energy states; therefore, the nucleus undergoes spontaneous decay with time in such a way that this excess energy is emitted forming new nuclide. A study of the characteristics of the naturally stable nuclides provides clues of instability factors of the radioactive nuclides. An N/Z diagram of the ‘line of stability’ relates the naturally stable nuclides extending from Z = 1 for hydrogen up to Z = 83 for ²⁰⁹Bi to those radioactive according to their neutron and proton numbers. Very long-lived nuclides are shown at the end of the line of stability although of their instability.

A major measure of nuclear stability is the neutron-proton ratio, as a result of the coulomb repulsion and exchange forces between them. Referring to Fig. 1.6 and closer look into light nuclei, the line of stability shows that neutron and proton numbers are equal (N ≈ Z). For heavy nuclei, the coulomb repulsion between the protons is substantial, and extra neutrons are needed to supply additional binding energy to hold the nucleons together. Thus, the line of stability shows N ≈ 1.5 Z, that is heavy stable nuclides have nearly 50 % more neutrons than protons. From Z > 83 all heavier nuclides are unstable. Radioactive nuclides surround the line of stability; nuclides lying above the line are said to be ‘proton deficient’, whereas nuclides lying below the line are ‘neutron deficient’. Radioactive nuclei attempt to reach the stability by different modes of radioactive decay which is going to be discussed later. In the N/Z diagram (Fig. 1.6), the excess-neutron number is seen as the vertical distance between the stable nuclides and the diagonal N = Z line. From the frequency distribution of stable isobars, isotopes and isotones, it has been concluded that even numbers of identical nucleons are more stable than odd numbers of the same nucleons (oddness of both Z and N tends to lower the nuclear binding energy).

Fig. 1.6

Neutron number (N) versus atomic number (Z) for nuclides found in nature. The deviation of the stable nuclei from the line of identity (i.e. Z = N) is obvious and has been attributed to an increase in neutron number to moderate proton repulsion

1.5 Production of Radiopharmaceuticals

Nuclear medicine is a unique medical specialty that uses radiopharmaceuticals for diagnostic or therapeutic purposes. The diagnostic role is to interrogate valuable functional information about disease biochemistry not only on the cellular or subcellular level but also extend to extract molecular and genetic information. The other good facet of nuclear medicine is its ability to target but treat critical diseases using therapeutic radionuclides. Diagnostic radiopharmaceutical is a radioactive drug that is administered in a tracer quantity with no pharmacological effect on human body. Radiopharmaceuticals can be broadly classified into two different categories, single photon emitters that are commonly used in conventional gamma camera imaging examinations and positron emitter-based radiopharmaceuticals. The former class of compounds are commonly labelled with ^99mTc solution eluted from molybdenum-99 generators. Radionuclides such as ²⁰¹Tl, ⁶⁷Ga, ¹¹¹In-, ¹²³I and ¹³¹I belong also to the same class and have several diagnostic or therapeutic applications.

The other class of radiopharmaceuticals are based on labelling with positron emitters (such as ¹⁸F, ¹¹C, ¹³N, ¹⁵O, etc.) and used in PET imaging applications such as oncology, cardiology and neurology. These kinds of radiotracers require medical cyclotrons and other essential infrastructures that include radiochemistry production facility, analytical and quality control equipments and other radiation detection and measurements devices. More details about medical cyclotron will be discussed later.

Since naturally occurring radioisotopes are relatively long half-lived and not handled well with human body, an artificially produced radioisotope which is cyclotron or reactor produced is being used. However, on-site radionuclide production is often required for positron emitter radionuclides with short half-lives such as ¹⁵O (2.04 min), ¹³N (10 min) and ¹¹C (20.38 min) which requires a local production to avoid loss of the material due to continuous decay. Since the radioisotopes need to be incorporated into some form of pharmaceutical, it should also be capable of being produced in a form which is amenable to chemical, pharmaceutical and sterile processing.

In March 2000, the fluorine-18-labelled glucose or F-18 fluoro-2-deoxyglucose (F-18 FDG) received Food and Drug Administration FDA approval for usage to evaluate and diagnose oncology patients although the first production was in 1978 for neurological applications. It is worth mentioning that first applications of FDG were focused on neurology and cardiac imaging, but its importance in oncology was realized on a later stage. F18-FDG limitations such as low specific targeting in PET imaging were an incentive for development of new PET tracers with special targeting capabilities. Newly developed PET traces are more specific and allow for imaging biological processes, such as angiogenesis, hypoxia, proliferation, apoptosis and many others. The expression of different receptors can be visualized like the somatization receptor 2, gene expression and dopamine and serotonin receptors in addition to large spectrum of potential cellular and molecular targets. Some of these approaches have found their way forward to the clinic, while others are still under extensive research and clinical evaluation.

1.5.1 Reactor Production Using Neutrons

Artificially produced radionuclide takes place in nuclear reactor by means of fission reaction or by using neutron flux to activate special target material located in reactor core. Naturally occurring radioactive material especially heavy nuclei (²³⁵U) undergoes spontaneous fission reaction; see Fig. 1.7. The result of such a reaction is two lighter fission fragments and few fission neutrons in addition to large amount of energy released. The fission neutrons will in turn initiate further fission reaction or what is called chain reaction. As the reactor uses the newly generated neutrons to keep fission reaction going on, on average one fission neutrons induce one more fission, so the process is self-sustaining chain reaction.

Fig. 1.7

Spontaneous fission reaction; ²³⁵U splits into two fission nuclei accompanied with neutrons release which in turn induce another fission reaction (chain reaction initiation)

Since N/Z ratio is high for fission fragments, it will undergo β⁻ decay until either stable nuclei are reached or relatively long half-life nuclide is reached and extracted from the reaction. The most important isotope produced in this way is ⁹⁹Mo which decays into ^99mTc through β⁻decay with half-life 2.75 days. The daughter nuclide (^99mTc) has very important clinical value in nuclear medicine and in wide variety of diagnostic examinations. The production of ⁹⁹Mo by a fission reaction is represented as ²³⁵U (n, f) ⁹⁹Mo.

In this reaction, uranium/aluminium alloy (containing uranium enriched to 45 % ²³⁵U) is used as target material. The typical yield of ⁹⁹Mo is in the order of (4–10 Ci) per g of ²³⁵U irradiated for 50–200 h in a neutron flux of 1.5 × 10¹⁴ n cm² s⁻¹.

Molybdenum-99 production can also take place through neutron activation in which target material (MoO₃) is irradiated by neutron flux (n, γ) reaction for 1 week.

$\begin{array}{l}\mathrm{M}\mathrm{o}{\left(n,\kern0.5em g\right)}^{99}\mathrm{M}\mathrm{o}\hfill \\ {}{}_{42}{}^{98}\mathrm{M}\mathrm{o}+{}_0{}^1n\to {}_{42}{}^{99}\mathrm{M}\mathrm{o}+\gamma \hfill \end{array}$

In this method of production, yield depends on neutron flux, neutron energy, target material and reaction activation cross section. Radionuclides production by (n, γ) reaction having poor specific activity as the produced nuclide and target material are isotopes and cannot be chemically separated. Other radionuclides used for diagnostic and therapeutic application in nuclear medicine such as¹³¹I, ¹⁵³Sm, ⁹⁰Y, ⁸⁹Sr, etc., are reactor produced.

1.5.2 Accelerator Production Using Charged Particles

Charged particle (protons, deuterons and alpha particles) accelerated by means of particle accelerator should possess sufficient kinetic energy to penetrate coulomb repulsion forces surrounding the nucleus. In this kind of radionuclide production, electrically charged particles are being accelerated to very high energy in range of MeV and then extracted towards target material initiating nuclear reaction for certain period of time in order to obtain sufficient amount of radionuclide. Radionuclide production takes place in charged particle accelerator by different nuclear reactions. The (p, n) reaction is one of the most reactions used for this purpose where irradiated atoms gain one proton accompanied by emission of neutron. The most common example is the production of F-18 from heavy water as shown here:

${}_8{}^{18}\mathrm{O}\left(p,n\right){}_9{}^{18}\mathrm{F}$

Another common nuclear reaction used is (d, n) in which the target nucleus will catch the accelerated particle (deuteron), subsequently the produced radionuclide atomic number and mass number each increases by one. The (d, n) reaction is given by:

${}_Z{}^AX\left(d,\ n\right){}_{Z+1}{}^{A+1}X$

An example of a radionuclide that is produced by deuteron irradiation is oxygen-15, and this reaction is written as

$\mathrm{N}{\left(d,\ n\right)}^{15}\mathrm{O}$

There are many different types of particle accelerator including the Van de Graaff accelerator, cyclotron, synchrocyclotron, synchrotron and linear accelerator although they are different types, but the main concept is still the same. Charged particles are accelerated in the presence of electric or magnetic field or both to reach the desired energy for extraction towards its target. Charged particle accelerators can produce radionuclides with high specific activity than reactor did.