Basics of Nuclear Medicine Physics and Radiation Safety
Kai Lee
LEARNING OBJECTIVES
1. Review of atomic structure.
2. Recognize the mechanisms of radioactivity and radiation.
3. Summarize the principles of radiation safety for compliant nuclear medicine practice.
THE ATOMIC STRUCTURE
An atom consists of a nucleus surrounded by layers of electrons (Fig. 1.1). The nucleus is made up of positively charged protons and electrically neutral neutrons. Electrons are negatively charged.
Atomic number (Z) is the number of protons. The mass number (A) is the sum of the number of protons and neutrons. Isotopes of an element have atoms with the same Z but different A and similar chemical properties. The convention for isotope nomenclature is shown in Figure 1.1 with X representing the chemical element.
The atomic number Z is often absent as the elemental symbol defines the number of protons. An isotope is referenced by its symbol followed by its mass number (e.g., Ga-67).
Chemical elements may have many isotopes. Nuclide refers to any atom with specific nuclear components. The term isotope refers to different nuclides of the same element. Nuclides may be radioactive (radionuclide) or stable.
Radioactive decay
Unstable radionuclides achieve stability through radioactive decay, which may be through alpha, beta, or positron emissions, and electron capture.
Alpha decay occurs in radionuclides with Z of 83 or higher. Alpha particle is a high kinetic energy (5-8 MeV), positively charged helium ion that travels a short distance (50-80 um) with high linear energy transfer of about 80 keV/um. The first approved alpha particle emitting radionuclide for treatment of bone metastases in men with castrate resistant prostate cancer is Ra-223 dichloride. Through alpha decay the parent Ra-223 transforms to daughter Rn-219 with emission of an alpha particle with a physical half-life of 11.4 days. The half-life of a radionuclide is the period during which 50% of the atoms of the parent radionuclide decays to the daughter nuclide.
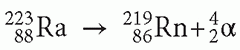
Rn-219 has two less neutrons and two less protons than Ra-223 (i.e., mass number A of Rn-219 is 4 less than Ra-223).
Beta particle emission typically occurs in radionuclides having a high neutrons to protons (N/P) ratio. An example of beta decay is the decay of P-32 to S-32 with the emission of a beta particle and an anti-neutrino.
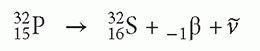
In beta decay, the mass number A of the daughter radionuclide remains the same since the atomic number Z increases by 1 and the neutron number decreases by 1. When the parent and daughter radionuclides have the same mass number A, they are referred to as isobars, and therefore beta decays are isobaric transitions. Figure 1.2 shows the decay of P-32 in a decay diagram that entails more detail than a decay equation. The horizontal axis in a decay diagram represents the atomic number Z, with Z increasing from left to right. The vertical axis represents the nuclide’s energy state. Each horizontal bar in the diagram represents a unique radionuclide.
Figure 1.2 demonstrates the decay scheme for P-32 as it becomes S-32 with the emission of a beta particle of maximum energy 1.71 MeV with a physical half-life of 14.3 days. Because the daughter, S-32 has one more proton than the parent P-32 the horizontal bar representing the daughter is to the right of P-32 as the atomic number Z of the daughter S-32 is increased by 1. The S-32 representation bar is below the P-32 bar because of the lower energy of the daughter nucleus. The mean beta energy is approximately one third of its maximum energy Emax (i.e., Eavg = Emax/3). With beta decay, the subatomic particle, neutrino that is also produced captures about two thirds of the released energy, and has infinitesimally small mass and no electrical charge. Some radionuclide also produce gamma radiation along with beta decay (e.g., Cs-137). The decay equation for Cs-137 is as follows:
Figure 1.3 shows the decay diagram for Cs-137. Cs-137 decays with a half-life of 30 years emitting a beta particle with a maximum energy Emax of 1.17 MeV in 5% of the decays, and a beta particle with Emax = 0.51 MeV in 95% of the decays. The unstable daughter Ba-137 releases its excess energy of 0.662 MeV as
gamma photon emission (vertical line; no change in Z, and A) and has one more proton than Cs-137 (horizontal line). It should be noted that there are no radionuclides that decay only through gamma emission. Gamma emissions are preceded by either electron capture, positron mission, and alpha or beta particle emission.
gamma photon emission (vertical line; no change in Z, and A) and has one more proton than Cs-137 (horizontal line). It should be noted that there are no radionuclides that decay only through gamma emission. Gamma emissions are preceded by either electron capture, positron mission, and alpha or beta particle emission.
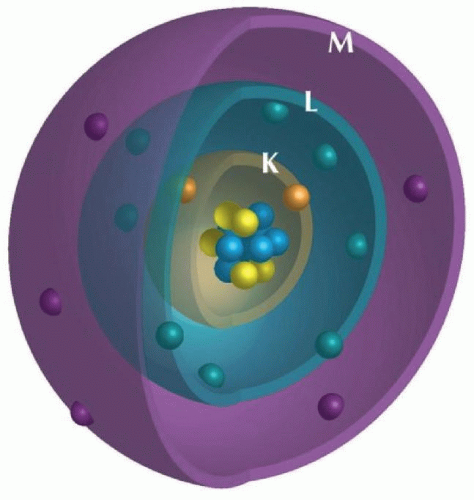 FIG 1.1 • A simple model of the atom has a nucleus of protons and neutrons surrounded by layers of electrons. Reprinted with permission from Lee (5). |
Isomeric transition
Figure 1.4 shows the decay scheme for Mo-99 with 12.5% of the decays through beta emission to yield Tc-99, and in the remaining 87.5% of the decays to produce Tc-99m, both daughters with the A and Z, but differ in the amount of nucleus energy. Tc-99m is a meta-stable radionuclide (hence the letter m after 99) that stays in transient high-energy state with half-life of 6 h emitting 140 KeV gamma photon to decay to Tc-99. Isomeric transition is the transition of a meta-stable nuclide from high-energy to low-energy state without change in A or Z.
Positron decay
Positrons (anti-matter) are similar to electrons (matter) except for their positive electrical charge. Radionuclides with low N/P ratio and sufficient excess energy (at least 1.02 MeV) may decay by positron emission by converting a proton to a neutron and generation of a neutrino as kinetic energy.
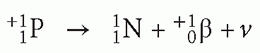
In the process of positron emission, the Z of the parent radionuclide decreases by 1, the A’s for both the parent and daughter remain the same, and the N/P ratio of the daughter nucleus is increased. F-18 decay is an example of positron decay.
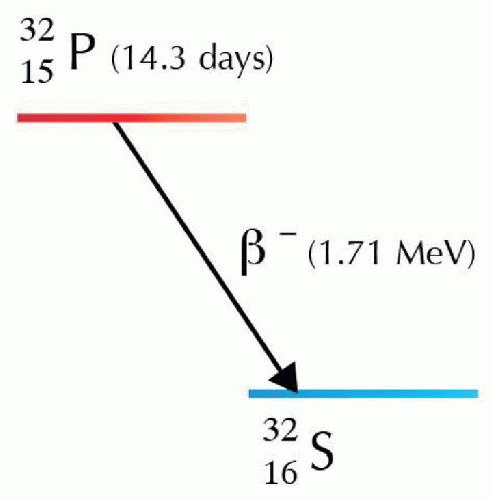 FIG 1.2 • The decay diagram is a graphical display of the series of events that occurs during the decay of a radionuclide. The atomic number Z increases from left to right in the horizontal axis, energy increases in the vertical axis. Each horizontal bar represents a nuclide. Reprinted with permission from Lee (5). |
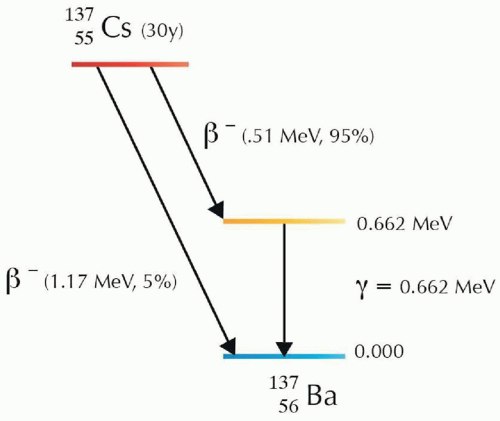 FIG 1.3 • The decay scheme of Cs-137. Reprinted with permission from Lee (5). |
In the decay scheme for F-18, the positron is emitted with Emax = 633 KeV and Eavg of about 250 KeV, with the neutrino representing the remaining kinetic energy (Fig. 1.5).
Positrons ejected from the nucleus lose their kinetic energy and collide with the electrons in the environment. The antimatter and matter annihilate each other, converting their masses to two 511 KeV annihilation photons emitted at approximately 180° from each other (Fig. 1.6). The mean free path is the average distance that is traveled by the positron from its origin before exhausting its kinetic energy and meeting an electron to annihilate with. The mean free path varies for different positron-emitting radionuclides. The mean free path for F-18 is about 1 mm, which is the theoretical resolution limit on imaging.
Electron capture
Electron capture is the mode of decay for radionuclides with low N/P ratios that do not have excess kinetic energy above 1.02 MeV. In electron capture, a neutron is generated by a proton capturing an electron from the atomic shell electron.
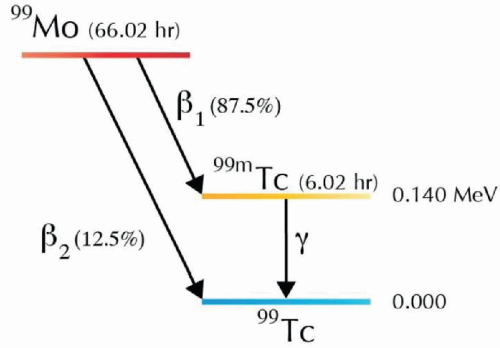 FIG 1.4 • Mo-99 in 87.5% of the beta decays goes to the metastable state Tc-99m. Tc-99m decays to Tc-99 in 6.02 h with emission of a 140 KeV photon. Reprinted with permission from Lee (5). |
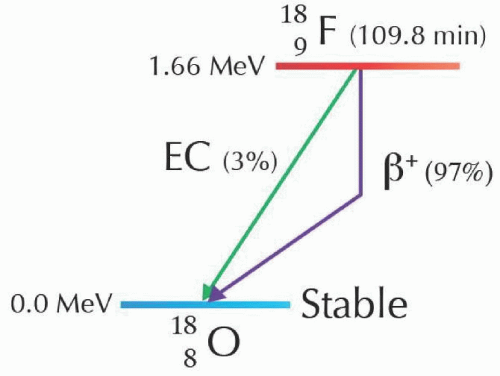 FIG 1.5 • F-18 decays either by positron emission or electron capture, 97% of the decays are by positron emission, and 3% by electron capture. Reprinted with permission from Lee (5). |
An example of electron capture decay is Iodine-123 (I-123) with the decay scheme shown in Figure 1.7. The decay of parent I-123 results in daughter Te-123 with a release of 159 KeV excess energy.
Characteristic X-rays
A characteristic x-ray (florescent x-ray) is released when an outer shell electron fills in an inner shell electron vacancy that occurs during electron capture by the nucleus. This released excess energy is due to the fact that the outer shells possess more energy than electrons in inner shell. This emitted x-ray is unique to a given atom therefore is called as characteristic x-ray. As an example, Tl-201 decay through electron capture emits characteristic x-rays spectrum of the daughter Hg-201 with a broad peak energy of 60 to 85 KeV (Fig. 1.8).
Radioactivity
The decay of a radionuclide is a random process and thus cannot be predicted in a moment of time, but a constant fraction of decay will occur over a specific unit of time at a decay rate called “radioactivity.” Radioactivity is defined as the product of this constant fraction decaying per unit time and the number of atoms present in the sample:

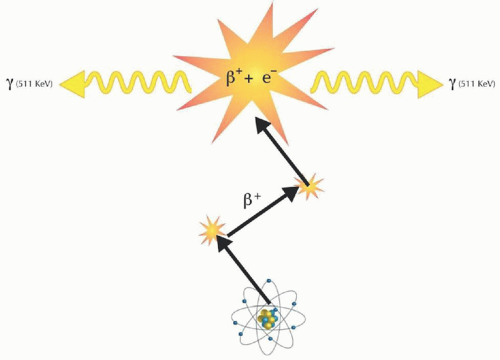 FIG 1.6 • The positron loses its kinetic energy after going through a series of interactions in a tortuous path and undergoes annihilation reaction with an electron. Reprinted with permission from Lee (5). |
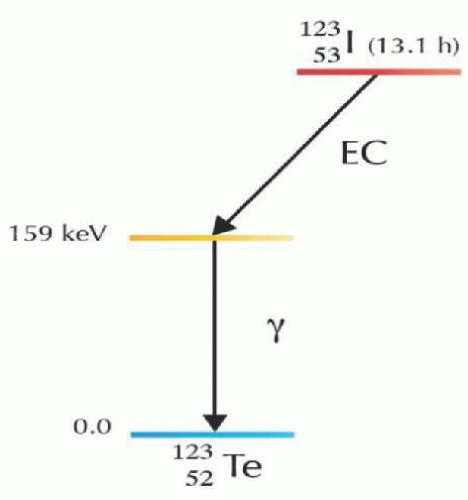 FIG 1.7 • The decay diagram of I-123. Notice that the arrow points to the left because the daughter Te-123 has one fewer proton than I-123. Reprinted with permission from Lee (5). |
where A is the symbol for radioactivity, or the rate of decay, λ is the decay constant, and N is the number of atoms in the sample. The fundamental unit for radioactivity is the number of atoms disintegrating per second (dps), which is the same as a Becquerel. The radioactivity unit Curie (Ci) is defined as follows:
1 Ci = 3.700 × 1010 dps = 3.7 × 1010 Bq
A millicurie (mCi) and a microcurie (uCi) are one-thousandth and one-millionth of a curie, respectively.
The decay constant λ, which is characteristic for a given radionuclide, is the fraction of the radioactive atoms in a sample decayed per unit time. The half-life of a radionuclide is the amount of time for 50% of the radioactive atoms in the sample to decay. Tc-99m has a half-life of 6.02 h, thus after 12.04 h, 25% remains, after 18.06 h 12.5%, and so on.
The relationship between the decay constant λ and T½ can be derived from the equation describing the amount of radioactivity remaining in the sample at a given time. The radioactivity At at time t in a sample of radionuclide behaves according to the exponential equation as follows:

In the previous equation, A0 is radioactivity in the sample initially. After one half-life t = T½, we get
At = 0.5 A0
Substituting the previous equation into Equation (1.2), and solving for λ the relationship between λ and T½ is
The half-life T½ of radionuclides are tabulated in references.
Universal decay table
The universal decay table is a table of the fractions that remain at selected time intervals since the time of calibration. The table is constructed using the equations in radioactivity calculations
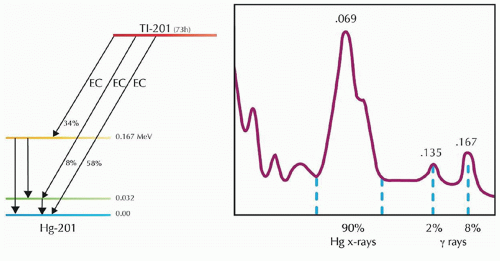 FIG 1.8 • Tl-201 decays by electron capture. The daughter is Hg-201 (left). The broad peak between 60 and 85 KeV are characteristic x-rays of Hg-201. The two small peaks at 135 and 169 KeV are gamma photons. Reprinted with permission from Lee (5).
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
 Get Clinical Tree app for offline access
Get Clinical Tree app for offline access

|