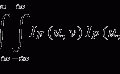For the distinction of clustered microcalcifications from normal tissues in mammograms, both NCs, such as microcalcifications, and LCs, such as blood vessels and mammary ducts, are important to be detected. To detect these components, we can employ the second derivative (Shimizu et al. 1994, 1995). The values of the second derivatives for nodular structure in all directions are negative. However, the value of the second derivative for the linear structure is zero along the direction of the axis of the linear structure, whereas it is negative along the direction perpendicular to the axis of the linear structure. Therefore, filters based on the second derivatives can be used for the detection or enhancement of nodular and linear structures. On the other hand, the minimal and maximal values of the second derivatives in all directions can be calculated using small eigenvalue λ ₁ and large eigenvalue λ ₂ of the Hessian matrix, because the second derivative of function f(x, y) in arbitrary direction θ is given by

Therefore, the following formulas indicate the conditions that must be satisfied by two eigenvalues λ ₁ and λ ₂ for nodular and linear structures, respectively:

For a nodular structure: λ ₁ ≅ λ ₂ < 0.

For a linear structure: λ ₁ < 0 , λ ₂ ≅ 0.

Figure 3.2 shows the filter bank based on the concept of the Hessian matrix for classifying nodular and linear structures. To obtain each element of the Hessian matrix using this filter bank, high-pass filter H _H (z), high-pass filter F _H (z), high-pass filter H _H (z)F _H (z), and smoothing filter H _L (z)F _L (z) at scale j are given by

By applying the smoothing filter H _L (z)F _L (z) to original image S ₀ f, smoothed subimage S ₁ f at the next scale, i.e., a scale of 1, is obtained. Horizontal subimage is obtained by applying high-pass filter H _H (z)F _H (z) at vertical direction, whereas vertical subimage is obtained by applying high-pass filter H _H (z)F _H (z) at horizontal direction. Diagonal subimage is obtained by applying high-pass filter H _H (z) at vertical direction followed by high-pass filter H _H (z) at horizontal direction.

In the filter bank shown in Fig. 3.2, NC _j (x, y) (the subimage for NC at scale j) was defined by the absolute value of large eigenvalue λ ₂ of the Hessian matrix at scale j. Here, if λ ₂ > 0, the pixels were zero because the eigenvalues for the nodular structure tend to become negative. NLC _j (x, y) (the subimage for NLC at the scale j) was defined by the absolute value of small eigenvalue λ ₁ of the Hessian matrix at the scale j. Here, if λ ₁ > 0, the pixels were zero.

We determined the eight features for distinguishing abnormal ROIs with clustered microcalcifications from two different types of normal ROIs without clustered microcalcifications (normal ROIs with blood vessels and normal ROIs without blood vessels). These eight features were extracted from the subimages for NC at scales from 1 to 4 and the subimages for NLC at scales from 1 to 4. Figure 3.3 shows the subimages for NC and for NLC, which were obtained from an abnormal ROI with clustered microcalcifications, normal ROI with blood vessels, and normal ROI without blood vessels. As shown in the subimages for NC, some pixel values for abnormal ROI were higher than those for two normal ROIs. As shown in the subimages for NLC, some pixel values for normal ROI without blood vessels were lower than those for abnormal ROI and normal ROI with blood vessels. The N features at each scale from 1 to 4 were determined using the average value of the pixel values higher than 97 % of the cumulative histograms of the subimage for NC at each scale from 1 to 4. The NL features at each scale from 1 to 4 were also determined using the average value of the pixel values higher than 97 % of the cumulative histograms of the subimage for NLC at each scale from 1 to 4.

To detect clustered microcalcifications, we employed the Bayes discriminant function (Duda et al. 2000) for distinguishing three classes ω _i  (i = 1, 2, 3). Classes ω ₁, ω ₂, and ω ₃ corresponded to abnormal ROI with clustered microcalcifications, normal ROI with blood vessels, and normal ROI without blood vessels, respectively. We divided our database into a training set and a test set. Each set included 600 mammograms obtained from 150 patients. We then trained the Bayes discriminant function using three different types of ROIs selected from the training set. The studied ROIs were 300 abnormal ROIs with clustered microcalcifications, 300 normal ROIs with blood vessels, and 300 normal ROIs without blood vessels. The normal ROIs were randomly selected from normal mammograms without clustered microcalcifications. In each of these three classes, the N and NL feature vector x at scales from 1 to 4 which were determined from each ROI were used for calculating mean vector m _i and covariance matrix V _i . Mean vector m _i and covariance matrix V _i are defined as

Here, n _i and Χ _i are the number of patterns and the pattern set in class ω _i , respectively. The Bayes discriminant function for distinguishing three classes ω _i  (i = 1, 2, 3) is given by
where |∙| is the determinant. Then we then selected the ROIs at intervals of approximately 1 mm in the test set. To distinguish the three types of ROIs, the eight features determined from the selected ROIs were inputted to the Bayes discriminant function as feature vector x. Bayes discriminant function g _i (x) outputted three values indicating the likelihood of each class. The class yielding the largest output value was considered as the result of the distinction of the three types of ROIs. Regions connecting the ROIs, which were classified as abnormal, were considered as regions with potential clustered microcalcifications.

A free-response receiver operating characteristic (FROC) curve (Metz 1989) is usually used to summarize the detection performance of a CADe scheme quantitatively. An FROC curve is a plot of the true-positive (TP) fraction achieved by a computerized scheme with respect to the average number of FPs per image varied over the continuum of a given threshold. In our case, the FROC curve is not easy to be calculated because the Bayes discriminant function output three values indicating the likelihood of each class. Therefore, first, we multiplied output value g ₁(x), indicating the likelihood of an ROI with clustered microcalcifications, by a coefficient before comparing g ₁(x), g ₂(x), and g ₃(x). Next, the ROI was considered abnormal when g ₁(x) was the highest value among the three output values. When the center of the region connecting the ROIs, which were classified as abnormal, was within a true cluster identified by an experienced radiologist, this region was considered “truly” detected. In this study, the coefficient was varied from 0.5 to 1.5.

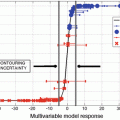
Figure 3.4 shows the relationship between the TP and the FPs obtained by applying the Bayes discriminant function with the eight features. For detecting clustered microcalcifications, many investigators have developed CADe schemes using the features related to the nodular structure only. Therefore, to investigate the usefulness of the NL features, the relationship between the TP and the FPs for the Bayes discriminant function with the four features, i.e., all features except for the NL feature, is also shown in Fig. 3.4. The detection performance of the Bayes discriminant function with the eight features is much higher than that of the Bayes discriminant function with the four features. The points, at which the blood vessels intersect, tended to become nodular in structure. Therefore, they were detected as FP candidates in many other algorithms for the detection of clustered microcalcifications. This result indicates that the number of these FP candidates is reduced by identifying the ROIs with blood vessels.

A CADe scheme based on the Bayes discriminant function with the eight features for distinguishing the three types of ROIs identifies 310 of the 310 clustered microcalcifications in the test set, yielding a sensitivity of 100.0 % and a false-positive rate of 0.98 per mammogram. Please refer to the paper (Nakayama et al. 2006a) for the details.

Freer and Ulissey (2001) prospectively assessed the effect of CADe on the interpretation of screening mammograms. In this study, 12,860 screening mammograms over a 12-month period were interpreted using a CADe system. The use of the CADe system resulted in the following: an increase in the recall rate from 6.5 to 7.7 %, no change in the positive predictive value for biopsy (38 %), an increase in the number of detected cancer incidents of 19.5 %, and an increase in the rate of detected early-stage cancer incidents from 73 to 78 %. Birdwell et al. (2005) studied prospectively 8682 women during a 19-month period. Approximately 10 % of 8682 patients were recalled using a CADe scheme. CAD-prompted recalls contributed to 8 % of total recalled findings and 7 % of detected cancer incidents. Ko et al. (2006) prospectively interpreted 5016 screening mammograms over a 26-month period without and with the use of a CADe system. With the CADe system, the recall rate increased from 12 to 14 %. The use of the CADe system had no significant effect on the positive predictive value for biopsy and could increase the cancer detection rate by at least 4.7 % and the sensitivity by at least 4 %. Gur et al. (2004) interpreted 115,571 screening mammograms with (n = 59,139) or without (n = 56,432) the use of a CADe system in an academic setting. They presented that the recall and breast cancer detection rates did not change significantly if the CADe system was used. Fenton et al. (2007) analyzed 429,345 mammograms for 222,135 women without and with the use of a CADe system. The use of the CADe system decreased the specificity from 90.2 to 87.2 %, increased the rate of biopsies by 19.7 %, and decreased the rate of the detection of invasive cancer by 12 %. They concluded that the CADe system reduces the accuracy of interpretation of screening mammograms. However, in this study, the use of the CADe system increased the sensitivity from 80.4 to 84 % (P = 0.32) and increased the rate of the detection of ductal carcinomas in situ by 34 %.

Even the same CADe schemes will demonstrate different sensitivities and specificities depending on the practice setting, number of the interpreted cases, experience of radiologists in mammogram interpretation, and experience of radiologists in the usage of the CADe scheme. These results are associated with an increase in sensitivity and with a decrease in specificity in screening mammography if a CADe scheme is used.

Most of the studies of CADx schemes focus on clustered microcalcifications and masses. There are few studies of CADx schemes for architectural distortions or bilateral asymmetries. Therefore, we only provide the information on CADx schemes for clustered microcalcifications and masses in this section. A CADx scheme consists of four main steps: image segmentation, feature extraction, feature selection, and classification.

Jiang et al. (1996) developed a method for differentiating malignant clustered microcalcifications from those benign. An ANN with eight computer-extracted features of clustered microcalcifications was employed to identify breast cancer. Computer analysis allowed to identify malignant clustered microcalcifications in 100 % cases and those benign in 82 % cases. The accuracy of computer analysis was statistically significantly better than that of five radiologists. Jiang et al. (1999) also extended this method of the classification of lesions as malignant or benign to multiple-view mammograms. Markopoulos et al. (2001) analyzed the malignancy of clustered microcalcifications using an ANN with eight features of the calcifications (density, number, area, brightness, diameter average, distance average, proximity average, and perimeter compacity average). They showed a statistically significant difference in the area under the ROC curve (AUC) values between the ANN (0.937) and the performance of physicians (0.810). Kallergi (2004) selected 13 classification features from descriptors of the morphology of the individual calcifications and the cluster distribution. The 13 features were combined with the age of patients and were given as inputs to an ANN. The classification performance reached a sensitivity of 100 % for a specificity of 85 %. Chan et al. (1998) developed computerized feature extraction of morphological features (size, contrast, and shape) and the texture features derived from the spatial gray-level dependence matrices. Linear discriminant classifiers with the features selected from the morphological features and the texture features were employed to evaluate the malignancy of clustered microcalcifications. They reported that the classifier could identify 50 % of the benign clusters at a sensitivity of 100 % for malignancy.

Huo et al. (1998, 2000) developed a computerized method for the classification of benign and malignant masses. The inputs to an ANN included four characteristics of masses (margin, sharpness, density, and texture) that were automatically extracted using an image-processing algorithm. The categorization of lesions as malignant or benign using the ANN achieved an AUC value of 0.90. Bilska-Wolak et al. (2003) compared the performance of a likelihood ratio-based algorithm (LRb) with respect to a case-based reasoning (CBR) classifier, which provided a solution to a new problem using past similar cases. The difference in the estimation of the probability density functions results in a very small difference in the performance. They reported that using both classifiers in approximately half of cases of benign mammographic masses, biopsy could be avoided at a sensitivity of 98 %. Brake et al. (2000) defined a number of features related to the image characteristics that radiologists use to distinguish real lesions from normal tissue. An ANN was used to map the computed features to a measure of suspiciousness of each region that was found suspicious using a mass detection method. Approximately 75 % of all cancer incidents were detected at a specificity level of 0.1 false positive per image. Floyd et al. (2000) proposed a case-based reasoning approach for the classification based on the ratio of the number of matched malignant cases to the number of total matches in the database. When 98 % of the malignancies would be biopsied, the number of benign biopsies would be decreased by 41 %.