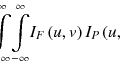Aristophanous et al. (2007) developed a pixel-clustering-based segmentation technique on selected PET tumor regions from non-small cell lung cancer patients. The general algorithm of the pixel-clustering-based segmentation approach with a Gaussian mixture model (GMM) to classify voxels into tumor and normal tissue voxels is described in this section. The clustering is referred to as “unsupervised learning” and does not require teacher signals (i.e., answers) as does “supervised learning” such as an artificial neural network. The basic idea of the pixel-clustering-based segmentation is to classify voxels into two classes, i.e., tumor and normal tissue voxels, by clustering the voxels according to the maximum a posteriori probability obtained by Bayes’ theorem (Aristophanous et al. 2007).

Let a region of interest (ROI) in an objective image be a vector x = (x ₁, x ₂,  … , x _N ), where x _i is the intensity at voxel i, and N is the number of voxels in the ROI. The voxel intensity is regarded as the random variable, which is assumed to be independent and identically distributed with a probability density function f(x _i ). Suppose that we have a set of K density functions, f _k (x _i | θ _k ), parameterized by θ _k , where k is the class number (k = 1 , 2 ,  …  , K; K, the number of classes), called component densities (or classes). Let the probability density function of the voxel intensity x _i given by θ _k be a Gaussian function, which can be expressed by
where μ _k and σ _k are the mean value and standard deviation in the kth class, respectively. Then, the probability density function of the voxel intensity x _i given by a parameter vector Ψ = (π ₁, π ₂,  … , π _K , θ ₁, θ ₂,  … , θ _K )(π _k , mixing proportions) is defined by
The mixing proportion π _k , which is regarded as the probability of belonging to a class k, satisfies the following conditions:
Let be a class random vector, where is defined as
The class random vector Z ⁽ⁱ⁾ follows a multinomial distribution. In accordance with Bayes’ theorem, the posterior probability that Z ⁽ⁱ⁾ = k when a voxel intensity x _i and a parameter vector Ψ are given is calculated by
This equation denotes the probability that the ith voxel belongs to the kth class. The final class of each voxel can be determined by the class, which has the maximum a posteriori probability among classes 1 to K. By using an expectation-maximization (EM) algorithm, from which the maximum likelihood parameters can be obtained, the parameter vector Ψ can be estimated by maximizing the following likelihood function:
At the Eth step, at first, the posterior probability P(Z ⁽ⁱ⁾ = k| x _i , Ψ) (Eq. 5.5) is calculated with the probability density function f _k (x _i | θ _k ) based on the initially clustered regions. Second, the expectation of a natural logarithm of the likelihood is obtained by using Eq. (5.6). At the Mth step, the parameter vector Ψ is updated based on new clustered regions. This iteration of E- and M-steps is stopped when the change in the logarithm of the likelihood is smaller than a threshold value.

The OCS method retrospectively determines a global optimum objective contour from multiple active delineations around a tumor. In addition, PET images are employed to determine the initial GTV regions to be used in the OCS method. First, the PET image is registered with the planning CT image through a diagnostic CT image of the PET/CT dataset by using an affine transformation (Jin et al. 2014). Initial GTV regions are obtained by thresholding the PET image at 80 % of the maximum standard uptake value (SUV_max) within a rectangular volume of interest (VOI), which has the same geometric position as the VOI in the planning CT image. Each initial GTV location is corrected in the VOI. Finally, the GTV region is segmented using the OCS method.

The SUV is employed for identification of the initial GTV regions, and is calculated as a ratio of the radioactivity concentration of tissue at a single time point to the injected dose of radioactivity concentration at that time point, divided by the body weight (Boellaard 2009):
where C represents the radioactivity concentration in kBq/ml obtained from the pixel value in the PET image multiplied by a cross calibration factor, D is the injected dose of 18-fluorodeoxyglucose (FDG) administered in MBq (decay corrected), and W is the body weight of the patient in kg.

The final GTVs are segmented by applying the OCS method to the initial regions, which are determined from the PET images. The basic concept of the OCS method is to retrospectively select a global optimum object contour from among multiple active delineations with a level set method around the tumors. In the OCS method, the level set method (LSM) (Sethian 1999) is employed for searching for the optimum object contour in the relationship between the average speed function value on an evolving curve and the evolution time.

An original level set equation of a partial differential equation (Sethian 1999) can be defined as
where ϕ(r(t), t) is the level set function, r(t) is the position vector at time t, and F is the speed function, which depends on circumstances on the evolution curve. The level set function is actually a distance image where the pixel values inside the initial curve are negative Euclidean distance values from each pixel to the closest pixel on the curve, but those outside the curve are positive distance values. The level set equation can be transformed into a Hamilton-Jacobi equation, which is equivalent to the Euler-Lagrange equation, as follows:
where H(F, ϕ(r(t), t), t)= F||∇ϕ(r(t), t)||, which is considered as a Hamiltonian. Solving (integration of a differential equation) a Hamilton-Jacobi equation of a contour involves the prediction of the contour with a minimum energy (possibly, a stable contour) from the analytical mechanics standpoint.

In the first step of the OCS method, the GTV contour and the speed function value obtained by the LSM are recorded at each evolution time from the initial GTV region until the evolution time reaches 10,000 or the evolving curve reaches the edge of the ROI in the planning CT image. The level set function φ(x, y, t) is updated from the initial GTV contour by using the following discrete partial differential equation:
where n is the evolution number, t is the evolution time, Δt is the evolution time interval, and F(x, y, t) is the speed function. The evolution time is the time of the contour deformation in updating the discrete partial differential equation. The zero level set of ϕ(x, y, t), which corresponds to the contour of the segmented region, moves according to the speed function F(x, y, t) in the three-dimensional level set function. The zero level set function, i.e., the evolving curve, moves according to the following speed function F(x, y, t):

where b(x, y) is the function of the edge indicator, G(x, y) is the Gaussian function, I(x, y) is the planning CT image to be processed, * denotes convolution, v is a constant, and κ(x, y, t) is the curvature. The edge indicator function b(x, y) and speed F (x, y, t) would be small around the edge, whereas the functions b(x, y) and F (x, y, t) would be large in relatively homogeneous regions.

In the second step, the GTV contour is determined from the optimum contour derived using the LSM by searching for the minimum point in the relationship between the evolution time and the average speed function value on an evolving curve, based on the steepest descent method (SDM). To avoid local minimum traps, the average speed function is smoothed by a median filter, and the smoothed function is resampled by a larger interval than the original one, before applying the SDM.

Figure 5.2a shows the relationship in the LSM between the evolution time and the average speed function value on an evolving curve. Figure 5.2b illustrates GTV contours, which were multiply delineated by the proposed method on the planning CT image of a lung cancer case. The average speed function as a function of the evolution time t converges to a global minimum of 4803. Therefore, the optimum contour can be determined by detecting the minimum point in the relationship between the average speed function and the evolution time.

The key idea of the machine-learning-based delineation (MLD) was to feed image features around GTV contours determined based on the knowledge or experiences of radiation oncologists into a machine learning classifier during the training step, after which the classifier produced the “degree of GTV” for each voxel in the testing step (Ikushima et al. 2016). The overall procedure of the MLD framework consists of the following four steps:

The SVM (Vapnik 1999) is one of machine learning techniques that can classify data into several (generally two) categories based on the output of a discriminant function. The SVM constructs a discriminant function in a linearly separable space by applying a nonlinear kernel function to a given training dataset. We consider a training dataset of training data and teacher signals, [x _i ,] (x _i  ∈ R ⁿ  , i , data number ; n , dimension ; i = 1 ,  …  , l , l , number of data, ), which we would like to classify. The discriminant function constructed by the SVM is expressed by (Vapnik 1999)
where x _i (i = 1 ,  …  , N , N, number of support vectors) is the support vector, b and α _i are parameters that determine the discriminant function, and K(x, x _i ) is the nonlinear kernel function, which can map a linearly non-separable dataset to a linearly separable dataset. The output was referred to as “degree of GTV” in this study.

The training procedure of construction of the SVM is shown as follows:

The efficacy of the proposed framework was evaluated in 14 lung cancer cases (solid, 6; ground glass opacity (GGO), 4; mixed GGO, 4) using the three-dimensional Dice similarity coefficient (DSC), which denotes the degree of region similarity between the GTVs contoured by radiation oncologists and those determined using the proposed framework. Figure 5.3 shows the planning CT, PET, and SVM-output images for three types of lung tumors. A tumor of the solid type has a high intensity with SUV_max of 7.75, but the GGO and mixed GGO types of tumors show low intensities with SUV_max of 1.09 and 1.62, respectively. On the other hand, the SVM enhanced not only the solid type of tumor but also the GGO and mixed GGO types of tumors in spite of low SUV_max. The proposed framework including the SVM and OCS method achieved an average DSC of 0.777 for 14 cases, whereas the OCS-based framework produced 0.507. The average DSCs for GGO and mixed GGO were 0.763 and 0.701, respectively, obtained by the proposed framework.

El Naqa et al. (2007) demonstrated the multimodality segmentation approach for delineating target regions by combining complementary information from different imaging modalities such as PET, CT, and MR systems and thus identifying GTV regions by simultaneously using anatomical and functional information. Their method was based on an active contour model without edges for vector-valued images (such as RGB or multispectral images) (Chan et al. 2000). The advantage of this model is to segment objects with different missing parts in different channels in a mutually complementary manner. El Naqa et al. took advantage of mutually complementary functions of the active contour model for vector-valued images such as medical multimodality images in a same coordinate system.

El Naqa et al. (2007) developed variational methods based on multivalued level set (MVLS) deformable models for simultaneous 2D or 3D segmentation of multimodality images consisting of combinations of coregistered PET, CT, or MR datasets. In their approach, a GTV region in an image I _i (x, y) for the ith imaging modality is segmented by minimizing the following energy function E with information of N images I _i (x, y) (i = 1 to N ; N, number of imaging modalities):