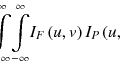In modern radiation therapy, the DRR technique is predominantly used in image-guidance systems to monitor the patient setup during clinical routines. The geometrical accuracy of the patient setup is guaranteed by superimposing a portal image of a megavoltage (MV) treatment beam or kV projection image acquired immediately prior to treatment onto the corresponding DRR created in the treatment planning. Thus, the common anatomical features on both images must be matched after the image registration. In this registration, various metrics, such as the least mean squares of the intensity difference, the normal cross correlation, and mutual information, can be employed. Each metric has advantages and disadvantages. Even if a metric is employed, the contrast mismatch between the portal image and the DRR affects the registration accuracy. Therefore, the generation of the DRR should be as realistic as possible, according to the fundamental physical process of the X-ray quanta (Staub and Murphy 2013).

The basic component of a DRR generation model is ray tracing with information on the linear attenuation coefficient from CT images. The observed projection in a detector element at a certain projection angle, y _i , is related to the corresponding photon count n _i as follows:
Here, M is the number of total projection elements given by the pixel number of the detector, and n ₀ is the constant photon number generated in the X-ray source. Assuming a monoenergetic spectrum in the X-ray beam, the relationship between the linear attenuation coefficient and the projection is linear, and the projection y _i can be evaluated by performing a line integral of the linear attenuation coefficient distribution μ(x) in 3D space vector x, along with a line between the X-ray source and the detector element i, as follows:
where the variable da is taken along with this line. The integration is approximately expressed by the summation of Δa _ij μ _j over j, which means the sampling point in the line, with the fact that Δa _ij is sufficiently small. The step size Δa _ij could be constant, but, with the use of CT voxels, it would be more efficient to calculate it analytically from the coordinates of X-ray source and detector element i. A schematic illustration is shown in Fig. 9.2, where μ _j and Δa _ij are the line attenuation coefficient and the length of the photon (which dives into the detector element i) trace in the voxel j, respectively. Although μ _j is converted from Hounsfield units (HUs) in CT, the X-ray energy in the IGRT system can differ from that in the treatment planning CT, and this conversion is possibly necessary. Here, the geometrical uncertainty of the X-ray source and detectors must be avoided. Uncertainty may arise with the use of an onboard FPD; therefore, the geometrical shift values should be measured in a QA/QC program and recorded for the correction for clinical imaging. This is one of the simplest ways to create a realistic DRR image.

The projection y _i can be influenced by additional physical effects. One such effect is the scattering, which is considerably large for FPDs in cone-beam projections. There are various methods for estimating the scattering, including experimental (e.g., beam stop arrays (Ning et al. 2004; Siewerdsen et al. 2004; Schörner et al. 2011; Zhu et al. 2009)), theoretical (e.g., scatter kernel methods (Yao and Leszczynski 2009a, b; Zhao et al. 2015), and Monte Carlo simulation (Zbijewski et al. 2006; Jarry et al. 2006) methods, as well as combinations of these. Another important effect influencing projections is beam hardening (Hsieh et al. 2000; Grimmer et al. 2009). In Eq. (9.2), a monoenergetic spectrum was assumed for an X-ray beam, but, the actual X-ray spectra are polyenergetic. As the X-ray passes deeply through the body of the patient, the spectrum becomes “hard” owing to the large cross sections for low X-ray energy. The scatter and beam-hardening corrections are discussed in the next subsection, where a simple correction method for CBCT reconstruction is introduced.

The other effects are relatively unimportant, but a rigorous reproduction requires them. One representative challenge for a realistic DRR is the consideration of the X-ray absorption due to the treatment couch, if a different couch is used in the treatment planning CT system. This attenuation is considered by inserting the virtual treatment couch. Other effects, such as veiling glare and signal leakage, can be considered in the DRR creation (Staub and Murphy 2013).

Since it was introduced by Jaffray et al., the CBCT system has taken on a very important role in IGRT (Jaffray et al. 2002; Dawson and Jaffray 2007; Létourneau et al. 2005; Boda-Heggemann et al. 2011). Figure 9.3 shows a typical cone-beam X-ray imaging system, which consists of a kV X-ray tube and an FPD unit perpendicular to the treatment MV beam, mounted on a LINAC gantry. Volumetric images can be reconstructed from 2D projection images on the FPD with a half rotation + fan angle range. Before the introduction of the CBCT imaging system, orthogonal pairs of portal images of the posterior–anterior and lateral directions using portal films or electric portal imaging devices (EPIDs) played the main role in the patient setup workflow (Mongioj et al. 2011; Birkner et al. 2007; Hawkins et al. 2011). In contrast, CBCT visualizes the anatomical information (shapes and locations) inside the body with a high contrast. After the in-room CBCT system was established, the accuracy of patient setup, i.e., the accuracy of dose delivery, drastically improved (Bujold et al. 2012).

In this subsection, the basic formalism of the CBCT reconstruction using an FPD is briefly introduced, but it can be easily extended to fan-beam CT and other geometrical cases. Further details are provided in the literature (Kak and Slaney 2001; Buzug 2008). First, we consider a parallel X-ray beam. As shown in Fig. 9.4, a projection P(θ, p) measured in the detectors aligned perpendicularly to the X-ray direction, p, in the projection angle θ, is expressed as
where δ(x) is the Dirac delta function, i.e., the line integral of the photon path, and f(x, y) is the 2D image of an object. The range of the integral for (x , y) is obvious—from the X-ray source to each detector element—and is therefore omitted throughout this chapter.

Equation (9.3) can be transformed as
where the integral range regarding projection angle θ is [0, π] and the kernel function h(x cos θ + y sin θ − p) is defined as

Equation (9.4) can be ascertained by multiplying both sides of Eq. (9.3) by h(x ^′ cos θ + y ^′ sin θ − p) and integrating them with respect to p, obtaining
Then, integrating the projection angle θ over the range of [0, π] yields Eq. (9.4), where the relation
is used (here, u = |ω| cos θ and v = |ω| sin θ).

The image f(x, y) is reconstructed by the convolution integral of the kernel h with the projection. Assuming a monoenergetic X-ray, the relation of the attenuation coefficient μ(x, y) in the object to observed photons is given as,
or
Here, n ₀ and n(θ, p) are the numbers of photon generated in the X-ray source and detected by the detector with (θ, p), respectively. A comparison with Eq. (9.3) reveals that the reconstructed image f(x, y) corresponds to μ(x, y) when y(θ, p) =  ln (n ₀/n(θ, p)) is used as P(θ, p).

The reconstruction formula for a parallel beam can be easily extended to a fan beam with a line-detector geometry. As exhibited by the geometry shown in Fig. 9.5, the projection of the off-axis beam SP is regarded as P(θ, p′) in the parallel-beam geometry. Therefore, the reconstruction formula can be represented as
where
By replacing the integrating variables θ and p′ with β and p, respectively, we obtain
where s =  − x sin β + y cos β, t = x cos β + y sin β, and the projection in the fan-beam geometry is expressed as .

Now, the formula for CBCT reconstruction with an FPD can be obtained by extending the aforementioned fan-beam CT reconstruction formula. The modifications are the distance from the source to the reconstruction points on the plane perpendicular to the s-axis (D ² + p ² → D ² + p ² + ζ ²), and the projection depends on the z-axis through ζ (see Fig. 9.6):
This is the final expression for the CBCT reconstruction. If ζ is fixed, the sinogram required in the reconstruction on the cone-beam projection is a line with v in the FPD corresponding to ζ. For instance, this formula reproduces the fan-beam reconstruction formula (Eq. (9.12) at ζ = 0, where the sinogram is constructed from the projection lines in the middle of the v-axis.

Well-known artifacts are observed in the LINAC-mounted CBCT reconstruction image. One of them is a “cupping artifact,” which is caused by several factors, the most dominant being the scattering of the X-ray for CBCT reconstruction using an FPD. Because of the photons scattered by the human body, the X-ray intensity measured in each pixel of the FPD becomes higher than that expected without scattering. This is more serious for the pixel in which the photon passes through the long range of highly dense materials. The CBCT formula described here does not consider any scattered photons. Therefore, when Eq. (9.13) is used in the reconstruction, the strategy of the correction is to remove the scattered photons in the measured projections. Although there are various methods for estimating the CBCT scattering, including beam stop aperture/moving blockers, scatter kernel models, and Monte Carlo simulation, one of the simplest methods is to multiply the detector count n(θ, p) by a factor κ  (0 < κ ≤ 1). Then, the corrected projection is obtained as
This means that the number of scattered photons in the detector decreases depending on the photon number. Thus, this factor can be used to correct the measured X-ray intensity, which is higher than that predicted with no photon scattering.

Figure 9.7 shows the effectiveness of this simple correction. Here, the cupping artifact shown in Fig. 9.7 (a) is visually corrected as shown in Fig. 9.7 (b). The center gray value profiles support this.

The beam-hardening effect may also yield a cupping artifact. The attenuation of an X-ray passing through the same tissue depends on the length of the path, owing to the change of the X-ray spectrum. Because a low-energy (soft) X-ray is attenuated more than a high-energy (hard) one, the magnitude of attenuation coefficient decreases as the path length increases. Thus, without beam-hardening correction, the measured X-ray intensity is always higher than the expected one. This also occurs in the case of scattering. The scattering and hardening of X-rays have similar influences on the projection image. Therefore, Eq. (9.14) can also be used for the correction of beam hardening. Of course, the physics differ between the two effects, and more quantitative corrections should be performed for both. There is a considerable amount of literature concerning beam hardening (Herman 1979; Nalcioglu and Lou 1979; Search et al. 1985; Hsieh et al. 2000; Ct et al. 2015).

Radar artifacts resulting from image lag are the other type of artifact commonly observed in CBCT. Image lag is defined as a residual signal present in image frames subsequent to the frame in which the residual signal is generated. The effect called “ghosting” (Mail et al. 2007) is similar to image lag and refers to the change in the detector pixel sensitivity as a long-term effect. Correction methods for image lag have been proposed in the literature. One of the practical methods is to subtract from the current projection frame previous frames weighted by a temporal response function (Mail et al. 2008). The reduction of the X-ray exposure on the detector using a “bow-tie filter” can be effective because the image lag depends on the X-ray intensity.

The geometrical uncertainty of the FPD, as well as the X-ray source during gantry rotation, causes the blurring of the reconstructed image. The distance between the center of the FPD and the projected point of the object pin located on the beam isocenter must be recorded for all projection angles, and it should be applied to correct the coordinates of the detector position or projection image. This is known as “flexmap correction” (Jaffray et al. 2002), and an example is shown in Fig. 9.8. Flexmap correction not only removes the blurring but also aligns the resulting image with the beam isocenter.

For periodic motions such as breathing or a heartbeat, motion-correlated CBCT images can be reconstructed by dividing projection images into several phase bins according to the motion signal (see Fig. 9.9). This technique is called “4D CBCT” and consists of four dimensions, including space (3D) as well as time. The 4D CBCT technique is widely utilized in IGRT, especially for SBRT requiring a more careful patient setup than the conventional treatment.

The acquisition time for the projection images in 4D CBCT is relatively long with a slow gantry rotation (typically 3–4 min) compared with normal 3D CBCT acquisition (1–2 min). This is because if the normal gantry rotation speed is used, the gantry-angle gap between the projection images becomes large in each phase bin, depending on the respiratory-cycle period, where the relationship between the gantry-angle gap (phase) Δθ [degrees] and the gantry rotation speed (angular velocity) v _gan [degree/s] is
Here, R _cycle [s] is the respiratory-cycle period. For example, in the condition of R _cycle = 3 s and 60 s for 360° rotation (v _gan = 6 [degree/s]), the gantry-angle gap Δθ is 18°. On the other hand, the typical gantry-angle gap for normal 3D CBCT is 0.5°–1.0°, assuming that the signal-acquisition interval of the FPD is 0.2 s. Such a large gantry-angle gap in acquiring projections for 4D CBCT yields a severe streak artifact in the reconstructed image. Thus, for the improvement of the image quality, the adaptation of slow gantry rotation is simple and effective.

Controlling the patient breathing can also reduce the artifacts. There are forced and unforced methods for this. Among the former, external breathing control is a representative example (Wong et al. 1999). This is performed with two pairs of flow monitors and scissor valves, by using one of each to control the inspiration and expiration paths to the patient through a mouthpiece. Among the latter methods, rhythmical sounds (e.g., metronome) or visual indications (e.g., Abches device) can be useful (Matsuo et al. 2013). Breath control is advantageous for 4D CBCT imaging, to reduce not only streak artifacts but also the blurring by stabilizing the breathing depth and cycle.

The 4D CBCT reconstruction method is based on the phase classification of acquired projections. Here, the knowledge of the respiratory phase during kV imaging plays a key role. There are several methods for measuring a respiratory signal synchronized with image acquisition, for example, external respiratory monitoring and real-time position management (Dietrich et al. 2006; Lu et al. 2007). Additionally, the utility of extracting respiratory signals using kV radiographs by monitoring the trajectory of a radio-opaque fiducial marker was reported (Li et al. 2006). Image-processing algorithms for projections obtained without external devices have been proposed by some groups. One such method is the “Amsterdam Shroud” (Fig. 9.10), which projects edge-enhanced projection images perpendicular to the axis of gantry rotation, leaving one-dimensional (1D) information in the cranio-caudal direction (Zijp et al. 2004). The advantage of the image-based recognition technique is that the respiratory signal can be detected with a high efficiency without an external system that synchronizes with projection images. The Amsterdam Shroud method was employed with the Elekta XVI system. Other methods are available, and respiratory-signal acquisition using the normal cross correlation with a limited area of projections was adapted to in-treatment 4D CBCT reconstruction performed during rotational treatment (Kida et al. 2012).

There are few methods for 4D CBCT reconstruction for nonperiodic motion. Nevertheless, a recent development of reconstruction methodology with compressive sensing (Donoho 2006) enables us to reconstruct images with a limited projection range. The prior image constrained compressive sensing (PICCS) method (Chen et al. 2008) and, more recently, a reconstruction method based on the chain-graph model (Nakano 2016) were proposed for slow-gantry-scan CBCT systems. An iterative reconstruction framework is needed for these methods, which requires a large computational cost. Therefore, the utility of this type of 4D CBCT is limited. It is suitable not for online patient registration but for post analysis, including margin analysis and dose verification.