Diffusion Magnetic Resonance Imaging in the Head and Neck

Diffusion weighting (DW) represents a magnetic resonance imaging contrast distinct from T1 and T2 in terms of imaging physics and its relationship to underlying physiology and pathophysiology. DW imaging has become a sine qua non of neuroimaging because of its exquisite sensitivity to the molecular motion of water that is altered in many pathologic conditions including acute ischemia. This article reviews the physical principles of DW imaging in the head and neck and describes how it can help to solve this and several other related problems.

Diffusion weighting (DW) represents a magnetic resonance (MR) imaging contrast distinct from T1 and T2 in terms of imaging physics and its relationship to underlying physiology and pathophysiology. Researchers have long been aware of DW imaging and although it is conceptually no more daunting than traditional MR imaging, it became practical only with the advent of higher performance field gradients. However, since its widespread deployment in the late 1990s, it has become a sine qua non of neuroimaging because of its exquisite sensitivity to the molecular motion of water that is altered in multiple pathologic conditions, including the classic example of impeded water motion in acute brain ischemia. More recently, because of the improvement in the spatial resolution and the postprocessing analytic tools of DW imaging, its utility as more than just a tool to evaluate for acute stroke has become apparent.

Continuous improvements in computed tomography (CT) and MR imaging have made the anatomic challenges of head and neck imaging less daunting. Now, the tumor size and extent can be reliably described, the macroscopic invasion of adjacent structures can be assessed, and the gross morphologic derangement of nodal architecture, including that of nodes in clinically inaccessible areas such as the retropharyngeal space, can be identified. Distinguishing normal physiology from more subtly disrupted diseased tissue and robustly characterizing the latter remain difficult. Often the radiologist is still forced to surrender the field to the surgeon and the pathologist, particularly in the posttreatment neck. Thus, there is an ongoing drive to develop more sophisticated, noninvasive biologic imaging techniques that evaluate tissue functional status (eg, cellularity, metabolic response to chemotherapy) to differentiate the areas of posttherapeutic ambiguous soft tissue that can be left alone (because they are nonneoplastic granulation tissue and are no-touch lesions) from those that need excision (because there is residual or recurrent neoplasm). This article reviews the physical principles of DW imaging in the head and neck and describes how it can help to solve this and several other related problems. Many excellent articles review the physical principles of DW imaging in greater detail.

Principles

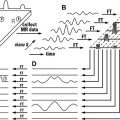
DW imaging measures the random motion of water protons by increasing the magnetic fields applied in opposite directions along a given axis. For example, consider a proton within a given voxel exposed to gradients such that if it moved along the x-axis in one direction from that voxel, it would experience increasingly positive field strength. Similarly, if it moved along the x-axis in the opposite direction, it would experience increasingly negative field strength. These gradients are symmetric such that the positive magnitude at a given distance in the x direction is equal to the negative magnitude at the same distance in the anti-x direction. In freely moving water, that is, water in which there are no impediments to diffusion, the same number of water protons (in a given voxel) move in the x and anti-x directions and for the same distance such that the positive and negative magnetic fields cancel each other out. Likewise, if there was a reason why water molecules within a voxel preferentially move in the x direction rather than the anti-x, then there would be a net positive magnetization from the increased number of protons moving along the x direction. Thus, DW is not based on inherent magnetization characteristics like T1 or T2 relaxation times but on a modification of local field strength by externally applied gradients. Therefore, the practical acquisition of DW images requires an underlying sequence (usually a T2-weighted echo planar sequence because of its speed) which is in turn modified by gradients applied not just in the x and anti-x directions but also in the y- and z-axes to assess for disruptions of free water flow in those directions as well. The need to piggyback the DW onto a spin echo sequence creates a problem in that the pure DW signal must then be extracted from the inherent T2 tissue contrast. The variety of methods of this disambiguation results, directly and indirectly, in the proliferation of DW images (DW imaging, apparent diffusion coefficient [ADC], exponential ADC, and so forth), which causes such consternation for radiology residents and neurologists.

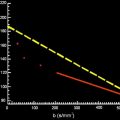
The signal intensity ( S ) measured in a DW voxel is calculated by the following formula:

<SPAN role=presentation tabIndex=0 id=MathJax-Element-1-Frame class=MathJax style="POSITION: relative" data-mathml='S=S0×exp(−b×D)’>S=S0×exp(−b×D)S=S0×exp(−b×D)
S = S 0 × exp ( − b × D )

where D is the diffusion coefficient, S ₀is the pure T2-weighted signal, and b is the diffusion sensitivity factor defined by the formula:

<SPAN role=presentation tabIndex=0 id=MathJax-Element-2-Frame class=MathJax style="POSITION: relative" data-mathml='b=γ2G2δ2(Δ−δ/3)’>b=γ2G2δ2(Δ−δ/3)b=γ2G2δ2(Δ−δ/3)
b = γ 2 G 2 δ 2 ( Δ − δ / 3 )

in which γ is the gyromagnetic ratio, G is the strength of the gradients applied along the given axes to assess for diffusion, δ is the width of those gradients, and Δ is their time. The true diffusion coefficient D cannot be controlled or measured directly by MR. Instead, an approximation, the ADC, must be calculated by measuring S with multiple b values and solving for the ADC algebraically.

In contrast to DW imaging, diffusion tensor imaging (DTI) not only generates the degree of freedom of diffusion (or diffusivity, a conceptualization akin to ADC) but also provides directionality to the diffusion characteristics within a voxel. It thus becomes possible to ascertain the direction of the diffusion vector in each voxel. Applying this principle, fiber tracts of a nerve or neural pathway can be delineated because the primary diffusion vector in a nerve or nerve bundle is oriented along the direction of its axon.

An alternative method, diffusion spectrum imaging (DSI), can evaluate multiple fiber orientations within a single voxel. Although DSI has promising applications within the complex white matter of the central nervous system, DTI is probably sufficient to identify the large peripheral nerves of the head and neck.

Protocols

Table 1 provides a sample neck diffusion protocol that is used at the authors’ institution at 3 T. This protocol is almost identical to that used for DW imaging of the brain and is based on a single-shot, spin echo, echo planar sequence with eddy current correction that can be performed rapidly, adding less than 2 minutes to the overall scan time. Images are acquired using the same 16-channel head and neck coil as for the rest of the scan, with the ADC images generated using the terminal hardware before transmission to the reading workstation.

Table 1

Only gold members can continue reading. Log In or Register to continue