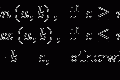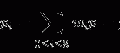Digital Images and Digital Myths

(1)

MGH Department of Radiology, Harvard Medical School, Newton, MA, USA

Abstract

Let’s begin with a short quiz.

Which of the following digital image transforms can be done without losing the original image quality?

Digital image zoom
Digital image rotation

Don’t rush, and think about this for a moment. Obviously, these two are the most essential image transformations. They give us the ability to handle digital images in the same way the pros from a bygone era used to work with old films—turning them around or looking at them through a magnifying glass. Clearly, the films were not altered. But what about the “soft copies”?

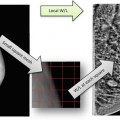
You might be surprised but both transforms, when applied to the digital images, will worsen their quality. The quality drop may not be visible, but this surely doesn’t mean that it doesn’t exist. Moreover, it’s cumulative: the more digital zooming and rotation you apply, the worse the images become (Fig. 2.1). Why?

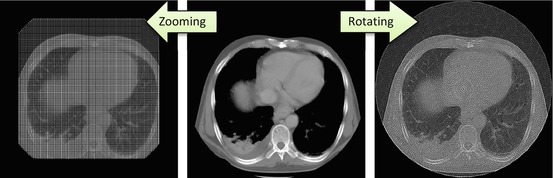
Fig. 2.1

Visualizing interpolation errors. The image in the center is the original; the image on the left is the result of 20 cumulative zooms by 20 % (in and out); the image on the right is the result of 20 cumulative rotations by 16 degrees (counter- and clockwise). In theory, left and right images should be identical to the original, as each transform was repeated to cancel itself. In reality however, each zoom or rotation has added invisible errors, accumulated into impossible-to-ignore distortion

The problem lies in the very nature of digital images. Unlike its analog film predecessor, a digital image is a very rigid structure; stored as a W × H matrix of integer¹ pixel values p _i, measured (sampled) at integer pixel locations (x _i,y _i): x _i = 1, … ,W (image width), and y _i = 1, … ,H (image height), as shown in Fig. 2.2. This grid of W × H integers p _i

Only gold members can continue reading. Log In or Register to continue