14.4. CHARACTERISTICS OF CLINICAL ELECTRON BEAMS
A. CENTRAL AXIS DEPTH DOSE
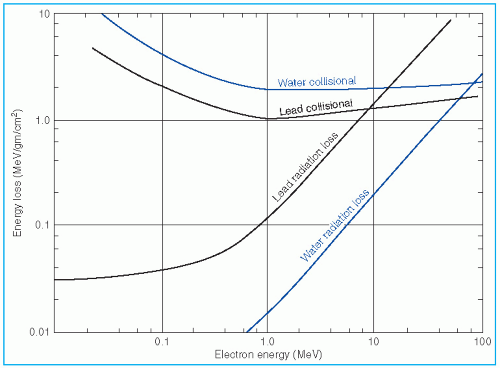
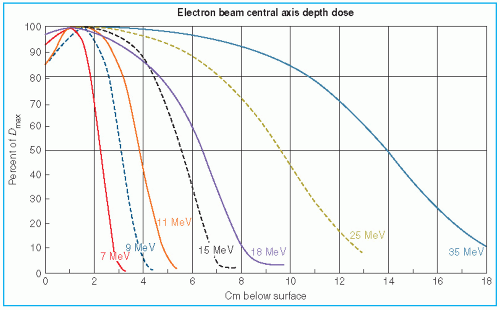
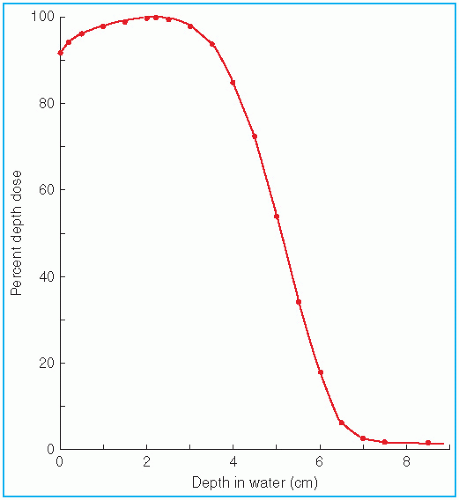
The major attraction of the electron beam irradiation is the shape of the depth dose curve, especially in the energy range of 6 to 15 MeV. A region of more or less uniform dose followed by a rapid dropoff of dose offers a distinct clinical advantage over the conventional x-ray modalities. This dose gradient, however, decreases with increasing energy.
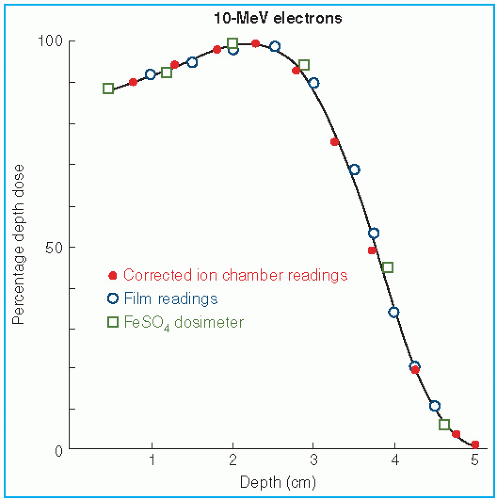
It was stated earlier that high-energy electrons lose energy at the rate of about 2 MeV/cm of water or soft tissue. Beyond the maximum range of electrons, the dose is contributed only by the x-ray contamination of the beam, indicated by the tail of the depth dose curve (
Fig. 14.8).
For a broad beam, the depth in centimeters at which electrons deliver a dose to the 80% to 90% isodose level is equal to approximately one-third to one-fourth of the electron energy in MeV. Thus, a 13-MeV electron beam is useful to a depth of about 3 to 4 cm, depending on the isodose level specified. As seen in
Figure 14.8, the depth dose curve falls off sharply beyond the useful depth and, therefore, the underlying tissues are spared.
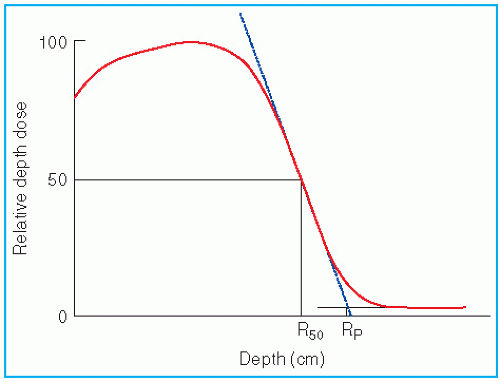
The most useful treatment depth, or therapeutic range, of electrons is given by the depth of the 90% depth dose. For modern accelerators with trimmer-type applicators this depth is approximately given by
E/3.2 cm, where
E is the most probable energy in MeV of the electron beam at the surface. The depth of the 80% depth dose occurs approximately at
E/2.8 cm. The depth of
Dmax does not follow a linear relationship with energy but it covers a broad region and its value may be approximated by 0.46 E
0.67 (
30).
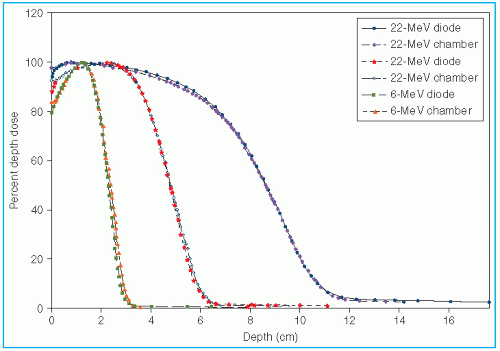
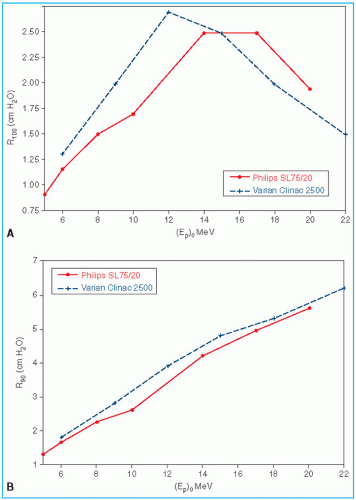
Figure 14.9 shows a comparison of depth of 90% dose (
R90) as a function of beam energy for two different linear accelerators. These differences can be clinically significant and, therefore, underscore the requirement of using beam data that have been measured specifically for the given machine.
The choice of beam energy is much more critical for electrons than for photons. Because the dose decreases abruptly beyond the 90% dose level, the treatment depth and the required electron energy must be chosen very carefully. The guiding principle is that, when in doubt, use higher electron energy to make sure that the target volume is well within the specified isodose curve.
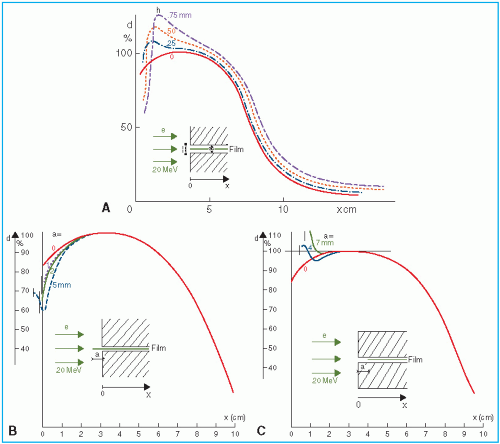
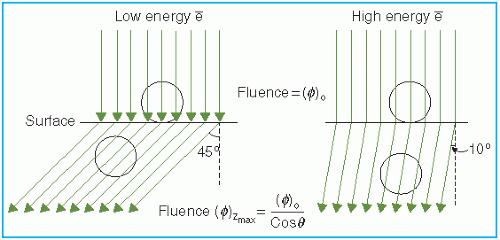
The skin-sparing effect with the clinical electron beams is only modest or nonexistent. Unlike the photon beams, the percent surface dose for electrons increases with energy. This effect can be explained by the nature of the electron scatter. At the lower energies, the electrons are scattered more easily and through larger angles. This causes the dose to build up more rapidly and over a shorter distance. The ratio of surface dose to maximum dose is, therefore, less for the lower-energy electrons than for the higher-energy electrons. A simple illustration of this effect is seen in
Figure 14.10. For the same incident electron fluence (
e−/cm
2), the lower-energy electrons build up to a larger fluence at the depth of maximum dose than the higher-energy electrons. The increase in fluence is given by 1/cos
θ, where
θ is the angle of scatter.
Because of differences in beam generation, beam bending, and collimation, the depth dose distribution and the surface dose can be significantly different for different machines.
Figure 14.11 illustrates this point by comparing central axis depth dose curves for the Sagittaire linear accelerator and the Siemen betatron for different beam energies. In clinical practice, therefore, it is not sufficient to specify just beam energy. Isodose distributions for an individual machine, cone, and/or field size are required.
B. ISODOSE CURVES
The scattering of electrons plays an important role in determining the shape of the isodose curves— the central axis distribution, flatness, and curvature near the field borders. Significant differences exist among the shapes of the isodose curves for different machines. These differences arise as a result of different collimation systems that the accelerators employ. The collimation system (e.g., scattering foil, monitor chambers, jaws, and cones) and the air column above the patient cause an angular dispersion of the beam as well as energy spread. Thus, two beams of the same energy, E0, can give rise to different dose distributions after passing through different collimation systems.
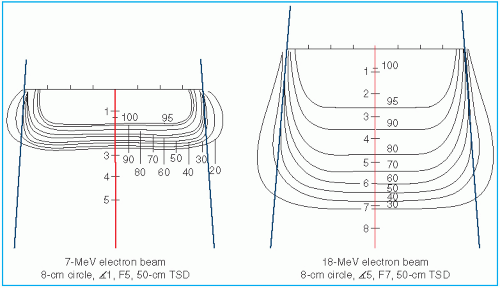
As the beam penetrates a medium, the beam expands rapidly below the surface due to scattering. However, individual spread of the isodose curves varies, depending on the isodose level, energy, field size, and collimation.
Figure 14.12 shows isodose patterns for two different energy beams. Whereas for the low-energy beams all the isodose curves show some expansion, for the higher energies only the low-value isodose levels bulge out. The higher isodose levels tend to show lateral constriction, which becomes worse with decreasing field size.
C. FIELD FLATNESS AND SYMMETRY
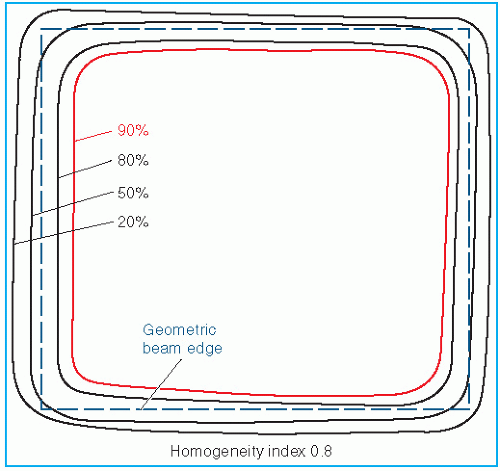
Uniformity of the electron beam is usually specified in a plane perpendicular to the beam axis and at a fixed depth. The ICRU (
31) specifies beam flatness in terms of a
uniformity index. This is defined in a reference plane and at a reference depth as the ratio of the area where the dose exceeds 90% of its value at the central axis to the geometric beam cross-sectional area at the phantom surface. The uniformity index should exceed a given fraction (e.g., 0.80 for a 10 × 10-cm field size and at depth of maximum dose). In addition, the dose at any arbitrary point in the reference plane should not exceed 103% of the central axis value.
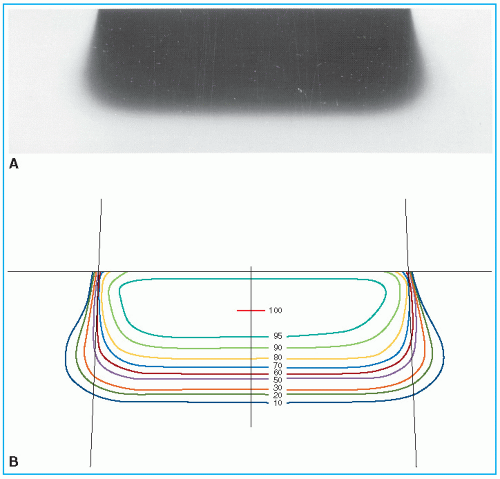
Figure 14.13 shows isodose curves obtained from a film exposed perpendicular to an electron beam at the depth of maximum dose. The dashed line is the boundary of the geometric beam at the surface. In this example, the homogeneity index is 0.8.
Because of the presence of lower-energy electrons in the beam, the flatness changes significantly with depth. Therefore, it has been recommended (
32) that the uniformity index be defined at the depth of half the therapeutic range (e.g., one-half the depth of 85% depth dose). Furthermore, it is defined as the ratio of the areas inside the 90% and 50% isodose lines at this depth. A uniformity index of 0.70 or higher is acceptable with field sizes larger than 100 cm
2. The peak value in this plane should be less than 103%.
The AAPM (
20) recommends that the flatness of an electron beam be specified in a reference plane perpendicular to the central axis, at the depth of the 95% isodose beyond the depth of dose maximum. The variation in dose relative to the dose at central axis should not exceed ±5% (optimally to be within ±3%) over an area confined within lines 2 cm inside the geometric edge of fields equal to or larger than 10 × 10 cm
2.
Beam symmetry compares a lateral dose profile on one side of the central axis to that on the other. The AAPM recommends that the cross-beam profile in the reference plane should not differ more than 2% at any pair of points located symmetrically on opposite sides of the central axis.
C.1. Beam Collimation
Acceptable field flatness and symmetry are obtained with a proper design of beam scatterers and beam-defining collimators. Accelerators with magnetically scanned beam do not require scattering foils. Others use one or more scattering foils, usually made up of lead, to widen the beam as well as give a uniform dose distribution across the treatment field.
The beam collimation has been significantly improved by the introduction of the dual-foil system (
33).
Figure 14.14 shows a typical arrangement for such a system. Whereas the first foil widens the beam by multiple scattering, the second foil is designed to make the beam uniform in cross section. The thickness of the second foil is differentially varied across the beam to produce
a desired degree of beam widening and flattening. Analysis by Werner et al. (
34) shows that the dual-foil systems compare well with the scanning beam systems in minimizing angular spread and, hence, the effect on dose distribution characteristics.
The beam-defining collimators are designed to provide a variety of field sizes and to maintain or improve the flatness of the beam. Basically, all collimators provide a primary collimation close to the source that defines the maximum field size and a secondary collimation close to the patient to define the treatment field. The latter can be in the form of trimmer bars or a series of different applicators. In the electron therapy mode, the x-ray collimator jaws are usually opened to a size larger than the applicator opening. Because the x-ray jaws give rise to extensive electron scatter, they are interlocked with the individual applicators to open automatically to a fixed predetermined size.
D. FIELD SIZE DEPENDENCE
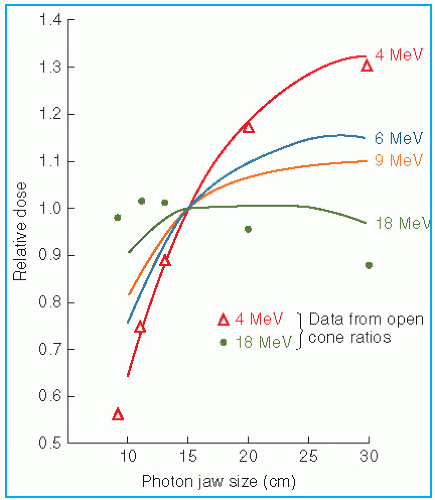
The output and the central axis depth dose distribution are field size dependent. The dose increases with field size because of the increased scatter from the collimator and the phantom. As stated previously, some electron collimators provide a fixed jaw opening, and the treatment field size is varied by various-size applicators (also called cones), inserts, or movable trimmer bars. Such an arrangement minimizes the variation of collimator scatter, and therefore, the output variation with field size is kept reasonably small. If the collimator aperture (x-ray jaw setting) were allowed to change with the treatment field, the output would vary too widely with field size, especially for lower-energy beams. This effect is shown in
Figure 14.15, where the applicator size is held fixed, while the x-ray jaws are varied (
35). Note that the dose rate varies by a factor of greater than 2 between small and large jaw openings at 4 MeV.
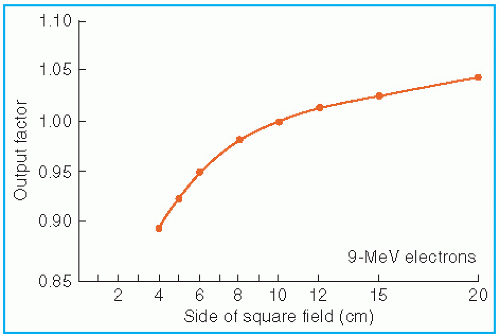
The effects of field size on output and the central axis depth dose curve due to phantom scatter is significant as long as the distance between the point of measurement and the edge of the field is shorter than the range of the laterally scattered electrons. After this distance is reached, there is no further increase in depth dose caused by phantom scatter. When the field size is reduced below that required for lateral scatter equilibrium (LSE), the dose rate decreases rapidly. This is shown in
Figure 14.16. In these measurements, the field size at the phantom was varied without changing the photon collimator opening. For small fields, the output factor as well as depth dose can be significantly reduced compared with the broad beam distribution.
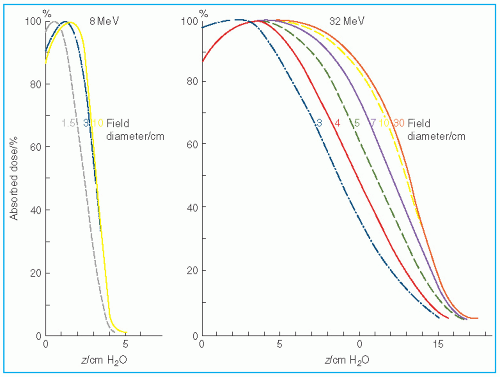
Figure 14.17 shows the change in central axis depth dose distribution with field size. As the field size is increased, the PDD initially increases but becomes constant beyond a certain field size when the LSE is reached. Furthermore, the depth
dmax shifts toward the surface for the smaller fields. Thus, in clinical practice, depth dose distribution for small fields should be measured individually in addition to the output calibration.
It has been shown (
36) that the minimum field radius for the establishment of LSE at all depths on central axis is given by the following approximate relationship:
where
Req is the field radius in cm and
Ep,o is the most probable energy at the surface in MeV. For example, the equilibrium fields for 8- and 32-MeV electrons have diameters of 5 and 10 cm, respectively, which agree with the data shown in
Figure 14.17. In clinical practice, the above relationship may be used to classify fields with radius less than
Req as small or narrow fields and radius greater than or equal to
Req as broad fields. Thus, as stated earlier, the depth dose distribution for small fields is field size dependent, while for broad fields it is independent of field size.
E. FIELD EQUIVALENCE
Exact field equivalence for electron beams of different shapes cannot be established. However, it has been shown (
36) that approximate equivalent circular or square fields can be determined for fields of any size, shape, and energy. The term
field equivalence means that for the same
incident fluence and cross-sectional beam uniformity, the equivalent fields have the same depth dose distribution along the central ray. Thus, field equivalence here is defined in terms of PDDs and not the output factors, which depend on particular jaw setting for the given applicator or other collimation conditions. According to this definition, all broad fields are equivalent because their depth dose distribution is the same irrespective of field size. For example, 10 × 10, 10 × 15, 10 × 20, and 20 × 20 are all broad fields for energies up to 30 MeV (see
Equation 14.11) and hence are equivalent in depth dose distribution. Field equivalence is therefore relevant only for small fields in which the LSE does not exist, and consequently, the depth dose distribution is field size dependent.
Harder et al. (
37) have shown that for a square field of dimensions (
a ×
a), the equivalent circular field has a diameter
Dequiv, given by
However, for small rectangular or irregularly shaped fields, field equivalence is not as straightforward. Khan and Higgins (
36) have applied Gaussian pencil beam theory to this problem and derived relationships that can be used to find approximate equivalent circular or square fields for fields of any size and shape. The reader is referred to their paper for further details on this subject.
F. SQUARE ROOT METHOD
Hogstrom et al. (
38) have shown that, if the change in collimator scatter with field size is not considered, the depth dose for rectangular field sizes can be extracted from square field data by the following relationship:
where D is the central axis depth dose and X and Y are the field dimensions. Thus, the depth dose for a rectangular field size can be determined from the square root of the two square field depth doses when the sides of the two square fields are equal respectively to the two sides of the rectangular field.
Referred to as the square root method, this concept has also been applied to the determination of output factors when the primary collimation is fixed and the secondary collimation close to the phantom is varied (
39). It may be restated that the collimator scatter is neglected in this model. Thus, the applicability of the square root method is not automatically valid for those machines in which collimator scatter varies significantly with field size.
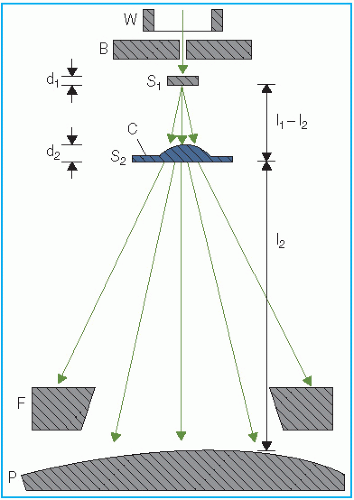
G. ELECTRON SOURCE
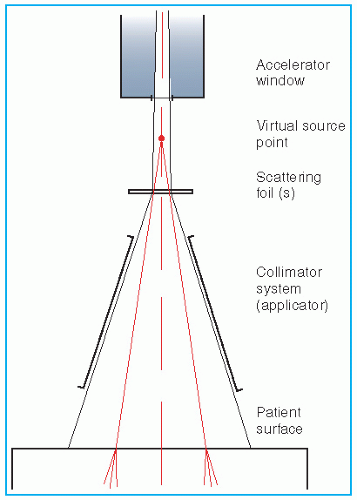
Unlike an x-ray beam, an electron beam does not emanate from a physical source in the accelerator head. A pencil electron beam, after passing through the vacuum window of the accelerator, bending magnetic field, scattering foils, monitor chambers, and the intervening air column, is spread into a broader beam that
appears to diverge from a point. This point is called the
virtual source (
40), which may be defined as an intersection point of the backprojections along the most probable directions of electron motion at the patient surface (
41). This is illustrated in
Figure 14.18.
A number of methods have been suggested for the determination of virtual source position. Pohlit’s (
40) method consists of taking electron radiographs of a grid of copper wires at different distances from the collimator and backprojecting the images to a point, the virtual source. A multipinhole technique (
41) uses double conical holes in a metal plate. Pinhole images are obtained on a film. Backprojection of the pinhole images gives the virtual source position. Meyer et al. (
42) have described the method of determining field size magnification on film with distance. The virtual source point is found by the backprojection of the 50% width of the beam profiles obtained at different distances. A broad beam (≥20 × 20 cm
2) is used for these measurements.
The use of virtual SSD does not give accurate inverse square law correction for output at extended SSDs under all clinical conditions. Measurements have shown that the virtual SSD gives correct inverse square law factor only for large field sizes (
43). For small field sizes, the inverse square law correction underestimates the change in output with virtual SSD. This deviation from the inverse square law is caused by an additional decrease in output because of a loss of side-scatter equilibrium in air and in phantom that is significant for small field sizes and low electron energies. Thus, the use of the virtual SSD to predict dose variation with distance requires correction factors, in addition to the inverse square law factor, as a function of field size and energy (
42).
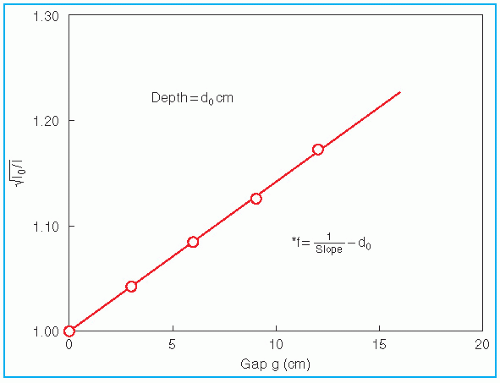
An alternative method of correcting dose output as a function of air gap between the electron applicator end and the patient is to determine a quantity known as the
effective SSD. The
effective SSD is defined as the distance from an effective source position to the standard phantom position (e.g., isocenter) which gives the correct inverse square law relationship for the change in output with distance. Khan et al. (
44) have recommended a method that simulates as closely as possible the clinical situation. In this method, doses are measured in a phantom at the depth of maximum dose (
dm), with the phantom first at the standard SSD (zero gap) and then at various distances, up to about 20 cm from the applicator end. Suppose
f = effective SSD,
I0 = dose with zero gap, and
Ig = dose with gap
g between the standard SSD point and the phantom surface. Then, if electrons obey inverse square law,
or
By plotting
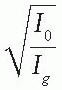
as a function of gap
g (
Fig. 14.19), a straight line is obtained, the slope of which is
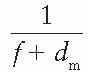
. Thus the effective SSD is given by
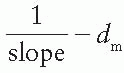
.
Although the effective SSD is obtained by making measurements at the depth
dm, its value does not change significantly with the depth of measurement (
44). However, the effective SSD does change with energy and field size, especially for small field sizes and low energies. A table of effective SSDs as a function of energy and field size may be made available as part of the beam data to meet clinical situations.
H. X-RAY CONTAMINATION
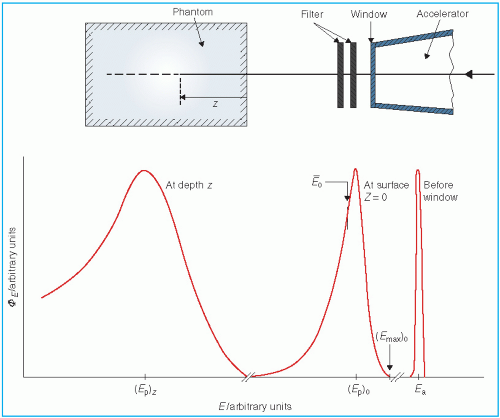
Dose due to x-ray contamination at the end of the electron range can be determined from the tail of the depth dose curve by reading off the dose value at the point where the tail becomes straight (
Fig. 14.3). This dose in a patient is contributed by bremsstrahlung interactions of electrons with the collimation system (scattering foils, chambers, collimator jaws, etc.) and the body tissues.
Table 14.2 gives the x-ray dose generated in water for monoenergetic electron beams, with no initial x-ray contamination. These values were extracted from the depth dose distributions in water calculated by Berger and Seltzer (
45), using a Monte Carlo program. The x-ray contamination dose from a medical accelerator, however, depends very much on its collimation system and is usually an order of two greater than the values given in
Table 14.2. In general, the x-ray contamination is least in the scanning beam type of accelerator, because the
scattering foils are not used. In a modern linear accelerator, typical x-ray contamination dose to a patient ranges from approximately 0.5% to 1% in the energy range of 6 to 12 MeV; 1% to 2%, from 12 to 15 MeV; and 2% to 5%, from 15 to 20 MeV.
For regular treatment field sizes used in electron beam therapy, the dose to the patient contributed by the x-ray contamination is not of much concern. However, even small amounts of x-ray contamination become critical for total skin electron irradiation such as in the treatment of mycosis fungoides (
Section 14.8).

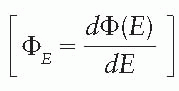 , the absorbed dose, D, is closely approximated by
, the absorbed dose, D, is closely approximated by
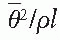 , where
, where 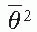 is the mean square scattering angle. Following the calculations of Rossi (13), mass scattering powers for various materials and electron energies have been tabulated (14).
is the mean square scattering angle. Following the calculations of Rossi (13), mass scattering powers for various materials and electron energies have been tabulated (14).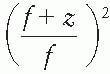 , where f is the effective source to surface distance (SSD); see Section 14.4E for details) and z is the depth. However, this correction in Rp is clinically not significant in terms of its impact on the ionization to dose conversion factor (20).
, where f is the effective source to surface distance (SSD); see Section 14.4E for details) and z is the depth. However, this correction in Rp is clinically not significant in terms of its impact on the ionization to dose conversion factor (20).

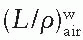 , as a function of mean electron energy at depth; and (b) chamber replacement correction, Prepl. This factor is dependent both on the air cavity diameter as well as well as the mean electron energy at the depth of measurement.
, as a function of mean electron energy at depth; and (b) chamber replacement correction, Prepl. This factor is dependent both on the air cavity diameter as well as well as the mean electron energy at the depth of measurement.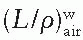 are provided in the Appendix (Table A.3) as a function of incident electron beam energy and depth. The factor Prepl accounts for three effects: (a) the in-scatter effect, which increases the electron fluence in the chamber cavity because of electron scattering out of the air cavity being less than that expected in the intact medium; (b) the obliquity effect, which decreases the fluence in the cavity because of electrons travelling relatively straight in the air cavity instead of taking oblique paths as they would without cavity owing to larger-angle scattering in the medium than air; and (c) the displacement in the effective point of measurement. The first two effects may be grouped into a fluence correction, while the third is called the gradient correction.
are provided in the Appendix (Table A.3) as a function of incident electron beam energy and depth. The factor Prepl accounts for three effects: (a) the in-scatter effect, which increases the electron fluence in the chamber cavity because of electron scattering out of the air cavity being less than that expected in the intact medium; (b) the obliquity effect, which decreases the fluence in the cavity because of electrons travelling relatively straight in the air cavity instead of taking oblique paths as they would without cavity owing to larger-angle scattering in the medium than air; and (c) the displacement in the effective point of measurement. The first two effects may be grouped into a fluence correction, while the third is called the gradient correction.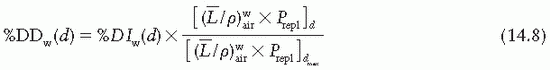
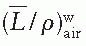 correction as a function of depth still needs to be applied.
correction as a function of depth still needs to be applied.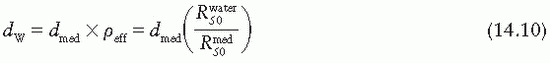


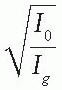 as a function of gap g (Fig. 14.19), a straight line is obtained, the slope of which is
as a function of gap g (Fig. 14.19), a straight line is obtained, the slope of which is 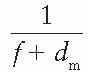 . Thus the effective SSD is given by
. Thus the effective SSD is given by 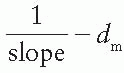 .
.