Field of View

Introduction

A pulse sequence diagram (PSD) provides a timing algorithm for the sequence of events that is carried out during an MR study. However, the operator must specify the dimensions of the desired part of the body under study. This is the subject of this chapter, namely, the field of view (FOV). As we shall see shortly, there is a limitation as to how small we can make the FOV, depending on the maximum strength of the gradients and the bandwidth of the received signals.

Field of View (FOV)

We’re going to discuss the relationship between the following entities:

FOV
Bandwidth
Gradients

Understanding these concepts is important because these features have definite clinical applications.

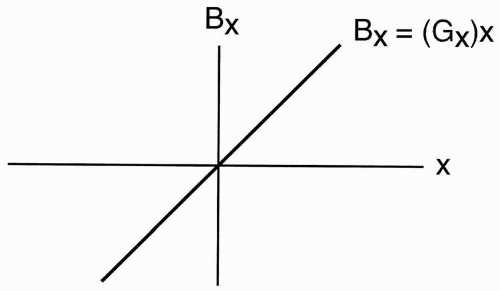
Let’s take an image with its x and y axes (Fig. 15-1). There is an FOV along the x-axis. Normally, we apply a gradient that increases as we move in the x direction (G_x). This means that we create magnetic inhomogeneities along the x-axis in a linear fashion. Consequently,

At the center point of the FOV, the magnetic field will be B₀.
On the right side of the FOV, the magnetic field will be greater than B₀.
On the left side of the FOV, the magnetic field will be less than B₀.

The magnetic field along the x-axis is B_x. The value of B_x is given by the linear equation: B_x = (G_x)x This equation shows that the value of the magnetic field at any point along the gradient (G_x) is the slope of the gradient (G_x) times the distance x along the x-axis (Fig. 15-2). Let’s multiply both sides of the equation by the gyromagnetic ratio γ: γ · B_x = γ(G_x)x
Recall that (γB_x) is the Larmor equation, which relates the magnetic field strength to the frequency: frequency_x = γB_x This equation states that the frequency of oscillation at any point along the x-axis is proportional to the magnetic field strength at that point, that is, f_x = γB_x or f_x = γ(G_x)x In other words, the frequency at any point along the x-axis is proportional to the slope of the gradient (G_x) multiplied by the position along the x-axis.

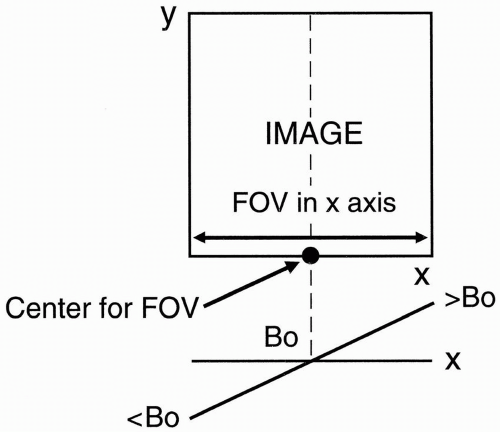Figure 15-1. An image with axes x and y. The frequencyencode gradient Gx causes the center of the field of view (FOV) to have magnetic field strength B0 and the right and left ends to have strengths greater and less than B0, respectively.

Figure 15-2. The gradient G_x describes a linear equation B_x = G_x · x. Therefore, at x = 0, no net magnetic field is added to the system, whereas at a positive value of x, a positive value of magnetic field is added to the main field.

Let’s see what happens at each end of the FOV (Fig. 15-3). At the right-side end of the FOV (i.e., at x = FOV/2), the frequency is maximum (call it f_max) because the Gx gradient, and therefore the magnetic field strength, is maximum.

The formula for frequency is f_x = γ(G_x)x Now, for f_max, the distance along the x-axis is ½ FOV. So, f_max = γ(G_x)FOV/2 Remember this is after we subtract the center frequency. Therefore, these measurements are centered around the zero frequency. At the opposite end of the gradient, we have −f_max: −f_max = −γ(G_x)FOV/2 What is the range of frequencies? The frequency range is from −f_max to +f_max, that is, Frequency range = −f_max → +f_max = ±f_max = 2f_max Another term for the range of frequencies is bandwidth (BW). Thus, BW = ±f_max = 2f_max

Only gold members can continue reading. Log In or Register to continue