History of Charged Particle Radiotherapy

Herman D. Suit

William Chu

Ernest Rutherford, Nobel laureate in 1908 in Chemistry, demonstrated the existence of the proton in 1919.¹,² Robert Wilson, Harvard University, made the first proposal that accelerated protons and heavier ions be considered for the radiation treatment of human patients. He published this proposal in the medical journal, Radiology.³ He wrote a personal account of his pioneering work in 1997.⁴ Figure 1.1 shows photographs of Rutherford and of Wilson.

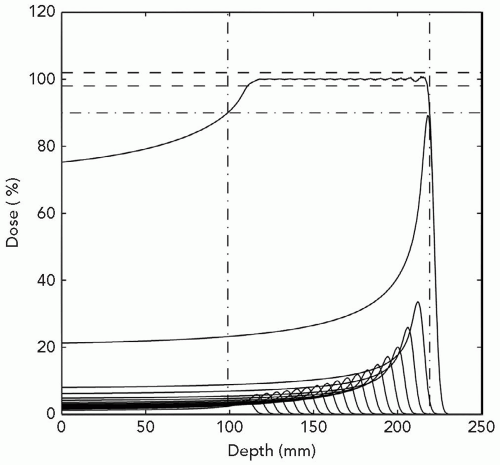
Wilson’s concept was that the dose versus depth graph is nearly flat to about the terminal 1 cm of the proton range, but then increases quite steeply and yields a distinct localized high-dose region that could be utilized to increase concentration of dose in the tumor. The peak at the end of the range in dose is referred to as the Bragg peak.⁵ Especially attractive is the fact that the dose is nearly zero deep to the distal aspect of the Bragg peak. For clinical application, the physicist merely needs to design a distribution of proton energies, that is, depths of the Bragg peaks, in order that there be a flat high-dose section just sufficient to cover the target. This is referred to as a spread-out Bragg peak, or SOBP. Examine Figure 1.2 for an illustration of the effect of layering of a graded series of proton energies. Further, examine Figure 1.3, a graphic display of depth-dose curves for a single proton and a photon beam. The excess dose for the photon beam relative to the proton is evident in the proximal region of the SOBP, the target volume where it shows a large gradient, and the distal region where it contributes a significant unwanted dose. This emphasizes the superiority of the proton relative to photon beams for external beam radiation therapy, namely, no dose deep to the target for each beam path and lesser dose proximal to the target, except for superficial lesions. These factors mean lower doses to normal tissues in the proton-treated patient. Accordingly, the tolerance of the patient should be increased and hence permit a higher dose to the target resulting in a higher tumor control probability (TCP) for a constant normal tissue complication probability (NTCP). Contrariwise, were the TCP by photon therapy considered acceptable, the dose to the target might be held constant but the reduced dose to adjacent normal tissues would lower NTCP for proton therapy. Importantly, technical options for proton therapy are equivalent to those for photon therapy. Specifically, proton therapy can employ as many beams, planar and non-coplanar, static or dynamic, conventional or intensity modulation as photon therapy.

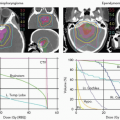
Figure 1.1 Ernest Rutherford (left) and Robert R. Wilson.

Figure 1.2 Individual pristine Bragg peaks of successively lower energies and intensities are combined to yield a spread-out Bragg peak whose dose distribution is characterized by an entrance dose region that builds up to a constant, near uniform (the horizontal lines indicated the 98%-100% interval) dose region, followed by a rapid fall-off in the distal region. The vertical lines define the distal range position (defined typically at the 90% value) and the proximal 90%; the width between the two vertical lines is referred to as the modulation width.

Experiments in laboratory animal systems permit employment of a range in dose levels that provide data for generation of complete dose-response curves, namely, response probabilities of <5% to >95%. This is, obviously, not feasible for any study of human normal tissue or tumor. Figure 1.4 is the dose-response curve on a logit linear dose plot, showing the logarithm of response probability versus dose, for local control of 8-mm mammary carcinoma of the C3H mouse growing as third-generation transplants in syngenic mice and treated by single-dose irradiation under conditions of local tissue hypoxia. The point is that any dose increment yields some increment in TCP; hence, the drive to utilize techniques that permit higher doses to the target. This shape of the dose-response curve is typical of findings on spontaneous tumors in the laboratory mouse and would almost surely apply to very narrow strata of human tumors (pathologic type, grade, and size) treated in a highly uniform manner and outcome scored accurately.

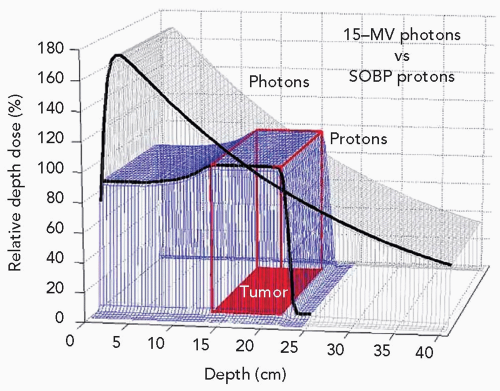Figure 1.3 Depth-dose distributions for a single field of 15-MV photons and an spread-out Bragg peak (SOBP) of 23-cm range and 12-cm modulation.

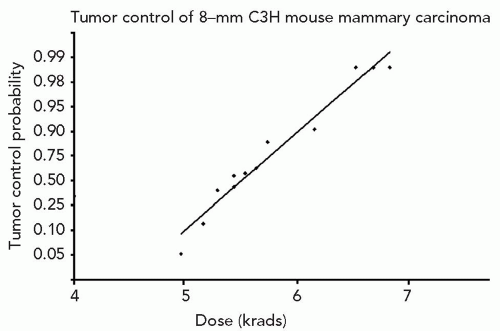Figure 1.4 Dose-response curve for local control of 8-mm C3H mouse mammary carcinoma as syngenic transplants treated by single-radiation doses under conditions of local tissue hypoxia.

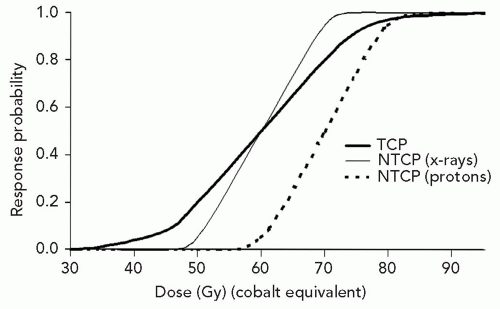
The rationale for pushing for higher doses is made clear by inspecting Figure 1.5, which presents dose-response curves for tumor control and NTCPs in a model system. The thick solid line is the dose-response curve for TCP by proton or photon irradiation with dose specified in relative biological effectiveness (RBE)-corrected dose units Gy (RBE). The TCP curve would be the same for photon
or proton irradiation. This curve is less steep than the two curves for NTCP. The solid thin line is designed to represent a large volume x-ray treatment and the dotted line for a smaller proton treatment volume (PTV). As shown, for NTCP of 0.05, the TCP for x-ray treatment is 20%, but for the proton treatment it is 50%. This is the result of the increased tolerance in the patient due entirely to the smaller volume of normal tissues receiving a high dose.

Figure 1.5 Dose-response curves for tumor control probability (TCP) (thick solid line) and for normal tissue complication probability (NTCP) (a thin solid line for large volume treatment and a dotted line for a reduced volume of irradiated normal tissues.)

THE PROTON

Protons are subatomic particles that, with neutrons and electrons, are the principal constituents of atoms since their formation not long after the Big Bang at ˜1.4 × 10¹⁰ years ago. Protons have a unit mass and a unit positive charge. Protons, themselves, are not primary particles in that they are comprised of three quarks (two up and one down) and gluons. In atoms of helium and greater mass, protons are approximately paired with neutrons. Neutrons have no charge and have approximately the same, though slightly higher, mass as protons. Their composition is also three quarks (one up and two down). There have been proposals that protons are not stable but on theoretic analyses have been predicted to have a finite half-life, which is in excess of 1032 years. A proton in a nucleus may decay into a neutron, a positron, and a neutrino.

DISCOVERY OF THE PROTON

In 1899, Rutherford discovered α and β “rays” from uranium. He later demonstrated that α rays are the nuclei of helium atoms.⁶,⁷ Rutherford discovered in 1911 that the nucleus of an atom constituted an extremely dense but small fraction of the volume of an atom and that this nucleus was positive in charge.⁸,⁹ This formed the basis of the model of the atom. Then after World War I, he demonstrated that irradiation of nitrogen gas by an α particle produced oxygen atoms and the nuclei of hydrogen atoms, namely protons.¹,² That is, the nucleus of the hydrogen atom was a single particle and had a positive charge of 1. He judged that this was a primary particle and gave it the name proton.¹⁰ This experiment showed that an atom of nitrogen was composed of a number of protons and electrons and that nitrogen could be artificially transmutated into oxygen and a nucleus of a free hydrogen atom.

Just 6 years later, James Chadwick discovered neutrons in 1932,¹¹ Robert Stone began clinical trials of fast neutron radiation therapy at Lawrence Berkeley Laboratory (LBL). Unfortunately, analysis of normal tissue reaction was assessed as indicating a significant frequency of severe late tissue injury.¹² Fast neutron therapywas later investigated at Hammersmith Hospital by Mary Catterall and her team.¹³ Many centers then commenced study of fast neutron therapy.

INITIAL PROTON RADIATION BIOLOGICAL STUDIES

Shortly after the end of World War II, E. Lawrence and associates constructed the “184-inch Synchrocyclotron” that could produce 340 MeV protons. E. Lawrence originally conceived the idea of the cyclotron early in 1929 after reading an article by Wideröe¹⁴ on high-energy accelerators. In the spring of 1930 he and one of his students, Edlefsen, constructed a cyclotron.¹⁵ Later in the fall of the same year, another student, M. Livingston, constructed a 13-cm diameter model that had all the features of early cyclotrons, accelerating protons to an energy of 80,000 eV (electron Volts) using <1,000 V on a semicircular accelerating electrode, now called the dee¹⁶,¹⁷ (see Fig. 1.6).

The first investigation of the biological effects of protons and deuterons were performed by Tobias et al.,¹⁸,¹⁹ on the 184-in. synchrocyclotron at the LBL. In 1952, they reported that the RBE for LD50 of “white mice” was approximately 1 for whole-body irradiation by 315 ± 15 MeV protons relative to 180 kVp x-rays. They further showed that highly localized deuteron irradiation of the rat pituitary by single doses of 190 to 250 Gy eliminated pituitary function. Figure 1.7 is a photograph of C. Tobias.

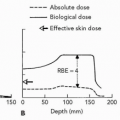
Injury of the central nervous system (CNS) (brain and spinal cord) by small-diameter proton beams was investigated by Larsson et al.,²⁰,²¹ Leksell et al.,²² and Rexed et al.,²³ in Sweden. At the Harvard Cyclotron Laboratory (HCL), Robertson et al.²⁴ conducted an intensive set of RBE determinations using the H4 mammalian cell line in vitro. For these experiments, the end point was loss of colonyforming ability and cell survival curves were determined. Measurements were made across a 5-cm SOBP and several
millimeters distal to the SOBP of a 160-MeV proton beam. The RBE was 1.0 for all positions except along the declining edge of the most distal Bragg peak. The RBE went to a maximum of 1.4 just distal to the peak of the most distal Bragg peak. The effect of these higher RBE values was to extend the biologically effective range of the beam by 1 to 2 mm. These points are illustrated by Figure 1.8A and B from Robertson et al.²⁴ This result is the effect of a reciprocal increase in RBE versus decrease in dose on that declining edge of the distal Bragg peak.

Only gold members can continue reading. Log In or Register to continue