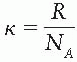Intensity-Modulated Radiation Therapy
20.1. INTRODUCTION
In the traditional external beam photon radiation therapy, most treatments are delivered with radiation beams that are of uniform intensity across the field (within the flatness specification limits). Occasionally, wedges or compensators are used to modify the intensity profile to offset contour irregularities and/or produce more uniform composite dose distributions. This process of changing beam intensity profiles to meet the goals of a composite plan is called intensity modulation. Thus, the compensators and wedges may be called intensity modulators, albeit much simpler than the modern computer-controlled intensity modulation systems such as dynamic multileaf collimators.
The term intensity-modulated radiation therapy (IMRT) refers to a radiation therapy technique in which a nonuniform fluence is delivered to the patient from any given position of the treatment beam to optimize the composite dose distribution. The treatment criteria for plan optimization are specified by the planner and the optimal fluence profiles for a given set of beam directions are determined through “inverse planning.” The fluence files thus generated are electronically transmitted to the linear accelerator, which is computer controlled, that is, equipped with the required software and hardware to deliver the intensity-modulated beams (IMBs) as calculated.
The clinical implementation of IMRT requires at least two systems: (a) a treatment-planning computer system that can calculate nonuniform fluence maps for multiple beams directed from different directions to maximize dose to the target volume while minimizing dose to the critical normal structures, and (b) a system of delivering the nonuniform fluences as planned. Each of these systems must be appropriately tested and commissioned before actual clinical use.
20.2. INTENSITY-MODULATED RADIATION THERAPY PLANNING
The principle of IMRT is to treat a patient from a number of different directions (or continuous arcs) with beams of nonuniform fluences, which have been optimized to deliver a high dose to the target volume and an acceptably low dose to the surrounding normal structures. The treatment-planning program divides each beam into a large number of beamlets and determines optimum setting of their fluences or weights. The optimization process involves inverse planning in which beamlet weights or intensities are adjusted to satisfy predefined dose criteria for the composite plan.
A number of computer methods have been devised to calculate optimum intensity profiles (1, 2, 3, 4, 5, 6, 7, 8, 9, 10). These methods, which are based on inverse planning, can be divided into two broad categories:
1. Analytic methods. These involve mathematical techniques in which the desired dose distribution is inverted by using a back projection algorithm. In effect, this is a reverse of a computed tomography (CT) reconstruction algorithm in which two-dimensional images are reconstructed from one-dimensional intensity functions. If one assumes that the dose distribution is the result of convolutions of a point-dose kernel and kernel density, then the reverse is also possible, namely by deconvolving a dose kernel from the desired dose distribution, one can obtain kernel density or fluence distribution in the patient. These fluences can then be projected onto the beam geometry to create incident beam intensity profiles.
One problem with analytical methods is that, unlike CT reconstruction, exact analytical solutions do not exist for determining incident fluences that would produce the desired dose distribution without allowing negative beam weights. The problem can be circumvented by setting negative weights to zero but not without penalty in terms of unwanted deviations from the desired goal. So some algorithms have been devised to involve both analytical and iterative procedures.
2. Iterative methods. Optimization techniques have been devised in which beamlet weights for a given number of beams are iteratively adjusted to minimize the value of a cost function, which quantitatively represents deviation from the desired goal. For example, the cost function may be a least square function of the form:
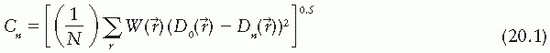
where Cn is the cost at the nth iteration, D0(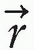 ) is the desired dose at some point
) is the desired dose at some point 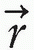 in the patient, Dn(
in the patient, Dn(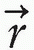 ) is the computed dose at the same point, W(
) is the computed dose at the same point, W(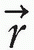 ) is the weight (relative importance) factor in terms of contribution to the cost from different structures, and the sum is taken over a large N number of dose points. Thus, for targets the cost is the root mean squared difference between the desired (prescribed) dose and the realized dose. For the designated critical normal structures, the cost is the root mean squared difference between zero dose (or an acceptable low dose value) and the realized dose. The overall cost is the sum of the costs for the targets and the normal structures, based on their respective weights.
) is the weight (relative importance) factor in terms of contribution to the cost from different structures, and the sum is taken over a large N number of dose points. Thus, for targets the cost is the root mean squared difference between the desired (prescribed) dose and the realized dose. For the designated critical normal structures, the cost is the root mean squared difference between zero dose (or an acceptable low dose value) and the realized dose. The overall cost is the sum of the costs for the targets and the normal structures, based on their respective weights.
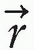 ) is the desired dose at some point
) is the desired dose at some point 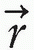 in the patient, Dn(
in the patient, Dn(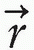 ) is the computed dose at the same point, W(
) is the computed dose at the same point, W(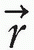 ) is the weight (relative importance) factor in terms of contribution to the cost from different structures, and the sum is taken over a large N number of dose points. Thus, for targets the cost is the root mean squared difference between the desired (prescribed) dose and the realized dose. For the designated critical normal structures, the cost is the root mean squared difference between zero dose (or an acceptable low dose value) and the realized dose. The overall cost is the sum of the costs for the targets and the normal structures, based on their respective weights.
) is the weight (relative importance) factor in terms of contribution to the cost from different structures, and the sum is taken over a large N number of dose points. Thus, for targets the cost is the root mean squared difference between the desired (prescribed) dose and the realized dose. For the designated critical normal structures, the cost is the root mean squared difference between zero dose (or an acceptable low dose value) and the realized dose. The overall cost is the sum of the costs for the targets and the normal structures, based on their respective weights.The optimization algorithm attempts to minimize the overall cost at each iteration until the desired goal (close to a predefined dose distribution) is achieved. A quadratic cost function such as that given by Equation 20.1 has only one minimum. However, when optimizing beam weights for all the beams from different directions to reach a global minimum, the same cost function may exhibit multiple local minima. Therefore, in the iteration process occasionally it is necessary to accept a higher cost to avoid “trapping” in local minima. An optimization process, called simulated annealing (3,10), has been devised that allows the system to accept some higher costs in pursuit of a global minimum.
Simulated annealing takes its name from the process by which metals are annealed. The annealing process for metals involves a controlled process of slow cooling to avoid amorphous states, which can develop if the temperature is allowed to decrease too fast. In the analogous process of simulated annealing, the decision to accept a change in cost is controlled by a probability function. In other words, if ΔCn <0, the change in the variables is always accepted. But if ΔCn >0, the change is accepted with an acceptance probability, Pacc, given by
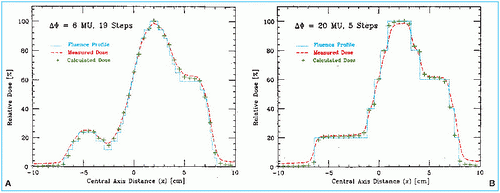
where ΔCn = Cn – Cn-1, κTn is analogous to thermal energy at iteration n (it has the same dimensions as ΔCn), Tn may be thought of as temperature, and κ is Boltzmann constant.1 At the start of simulated annealing, the “thermal energy” is large, resulting in a larger probability of accepting a change in variables that gives rise to a higher cost. As the optimization process proceeds, the acceptance probability decreases exponentially in accordance with Equation 20.2 and thus drives the system to an optimal solution. The process is described by Web (10) as being analogous to a skier descending from a hilltop to the lowest point in a valley.
The patient input data for the inverse planning algorithm are the same as that needed for forward planning, as discussed in Chapter 19. Three-dimensional image data, image registration, and segmentation are all required when planning for IMRT. For each target [planning target volume (PTV)], the user enters the plan criteria. These may include maximum dose, minimum dose, and/or dose volume objective(s). For the critical structures, the user may enter the desired maximum dose and/or dose volume objective(s). Depending on the IMRT software, the user may be required to provide other data such as beam energy, beam directions, number of iterations, etc., before proceeding to optimizing intensity profiles and calculating the resulting dose distribution. The evaluation of an IMRT treatment plan also requires the same considerations as the “conventional” three-dimensional conventional radiotherapy (3-D CRT) plans, namely viewing isodose curves in orthogonal planes, individual slices, or 3-D volume surfaces. The isodose distributions are usually supplemented by dose volume histograms.
After an acceptable IMRT plan has been generated, the intensity profiles (or fluence maps) for each beam are electronically transmitted to the treatment accelerator fitted with appropriate
hardware and software to deliver the planned IMBs. The treatment-planning and delivery systems must be integrated to ensure accurate and efficient delivery of the planned treatment. Because of the “black box” nature of the entire process, rigorous verification and quality assurance procedures are required to implement IMRT.
hardware and software to deliver the planned IMBs. The treatment-planning and delivery systems must be integrated to ensure accurate and efficient delivery of the planned treatment. Because of the “black box” nature of the entire process, rigorous verification and quality assurance procedures are required to implement IMRT.
20.3. INTENSITY-MODULATED RADIATION THERAPY DELIVERY
Radiation therapy accelerators normally generate x-ray beams that are flattened (made uniform by the use of flattening filters) and collimated by four moveable jaws to produce rectangular fields. Precollimation dose rate can be changed uniformly within the beam but not spatially, although the scanning beam accelerators (e.g., Microtron) have the capability of modulating the intensity of elementary scanning beams. To produce intensity-modulated fluence profiles, precalculated by a treatment plan, the accelerator must be equipped with a system that can change the given beam profile into a profile of arbitrary shape.
Many classes of intensity-modulated systems have been devised. An ASTRO-AAPM Collab-orative Working Group (11) has classified IMRT delivery techniques into a number of categories. These include scanned photon and electron beams, tomotherapy IMRT, conventional MLC IMRT, physical modulator IMRT (i.e., compensators), and robotic linear accelerators. For linear accelerators, it seems that the computer-controlled MLC is the most practical device for delivering IMBs, and is by far the most frequently used delivery mechanism. IMRT delivery with MLCs may be classified into three groups: Delivery systems that use fixed gantry angles, rotating fan beams (tomotherapy), and rotating cone beams (12). We will discuss each of these MLC-based delivery systems in the following sections.
A. IMRT WITH FIXED GANTRY ANGLES
For a given gantry angle, a computer-controlled multileaf collimator is not only useful in shaping beam apertures for conventional radiotherapy, but it can also be programmed to deliver IMRT. This has been done in two different ways.
A.1. Segmental MLC Delivery
In segmental MLC (SMLC) delivery, the patient is treated by multiple fields and each field is subdivided into a set of subfields irradiated with uniform beam intensity levels. The subfields are created by the MLC and delivered in a stack arrangement one at a time in sequence without operator intervention. The accelerator is turned off while the leaves move to create the next subfield. The composite of dose increments delivered to each subfield creates the IMB as planned by the treatment-planning system (TPS). This method of IMRT delivery is also called “step-and-shoot” or “stop-and-shoot.” The theory of creating subfields and a leaf-setting sequence to generate the desired intensity modulation has been discussed by Bortfeld et al. (13). The method is illustrated in Figure 20.1 for one-dimensional intensity modulation in which a leaf pair takes
up a number of static locations and the radiation from each static field thus defined is delivered at discrete intervals of fluence (shown by dotted lines). In this example, 10 separate fields have been stacked in a leaf-setting arrangement known as the “close-in” technique (Fig. 20.2A). Another arrangement called the “leaf sweep” is also shown (Fig. 20.2B). The two arrangements are equivalent and take the same number of cumulative monitor units (MUs). In fact, if N is the number of subfields stacked, it has been shown that there are (N!)2 possible equivalent arrangements (14). The two-dimensional intensity modulation is realized as a combination of multiple subfields of different sizes and shapes created by the entire MLC.
up a number of static locations and the radiation from each static field thus defined is delivered at discrete intervals of fluence (shown by dotted lines). In this example, 10 separate fields have been stacked in a leaf-setting arrangement known as the “close-in” technique (Fig. 20.2A). Another arrangement called the “leaf sweep” is also shown (Fig. 20.2B). The two arrangements are equivalent and take the same number of cumulative monitor units (MUs). In fact, if N is the number of subfields stacked, it has been shown that there are (N!)2 possible equivalent arrangements (14). The two-dimensional intensity modulation is realized as a combination of multiple subfields of different sizes and shapes created by the entire MLC.
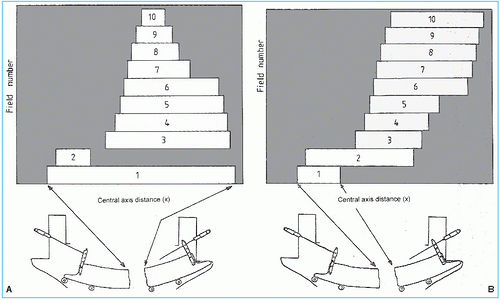 Figure 20.2. Ten separate fields are stacked to generate the beam profile shown in Figure 20.1. Multileaf collimator leaves are shown schematically below the fields: A: leaf setting as “close-in” technique; B: leaf settings as “leaf-sweep” technique. (From Web S. The Physics of Conformal Radiotherapy. Bristol, UK: Institute of Physics Publishing; 1997:132, with permission.) |
The advantage of the step-and-shoot method is the ease of implementation from the engineering and safety points of view. A possible disadvantage is the instability of some accelerators when the beam is switched “off” (to reset the leaves) and “on” within a fraction of a second. The use of a gridded pentode gun could overcome this problem as it allows monitoring and termination of dose within about one-hundredth of a MU. However, not all manufacturers have this type of electron gun on their linear accelerators.
A mixed mode of IMB delivery, called “dynamic-step-and-shoot,” has also been used. In this method the radiation is “on” all the time, even when the leaves are moving from one static subfield position to the next. This technique has the advantage of blurring the incremental steps in the delivery of static subfields (15).
Bortfeld et al. (13) have demonstrated that a relatively small number of steps (10-30 to cover a 20-cm wide field) can be used to deliver an intensity-modulated profile with an accuracy of 2% to 5%. A nine-field plan could be delivered in less than 20 minutes, including extra time allowed for gantry rotation (13). Figure 20.3 is an example of an intensity-modulated fluence profile generated by the step-and-shoot method and compared with calculated and measured dose.
A.2. Dynamic MLC Delivery
In this technique the corresponding (opposing) leaves sweep simultaneously and unidirectionally, each with a different velocity as a function of time. Unlike SMLC delivery, the accelerator beam is on while the leaves are moving. The period that the aperture between leaves remains open (dwell time) allows the delivery of variable intensity to different points in the field. The method is known as dynamic MLC (DMLC), and is sometimes called “sliding window.”
The leaves of a DMLC are motor driven and are capable of moving with a speed of greater than 2 cm/sec. The motion is under the control of a computer, which also accurately monitors
the leaf positions. The problem of determining leaf velocity profiles has been solved by several investigators (16,17). The solution is not unique but rather consists of an optimization algorithm to accurately deliver the planned intensity-modulated profiles under the constraints of maximum possible leaf velocity and minimum possible treatment time.
the leaf positions. The problem of determining leaf velocity profiles has been solved by several investigators (16,17). The solution is not unique but rather consists of an optimization algorithm to accurately deliver the planned intensity-modulated profiles under the constraints of maximum possible leaf velocity and minimum possible treatment time.
The basic principle of dynamic collimation is illustrated in Figure 20.4. A pair of leaves defines an aperture with the leading leaf 2 moving with velocity V2(x) and the trailing leaf 1 with velocity V1(x). Assuming that the beam output is constant with no transmission through the leaves, penumbra, or scattering, the profile intensity I(x) as a function of position x is given by the cumulative beam-on times, t1(x) and t2(x), in terms of cumulative MUs that the inside edges of leaves 1 and 2, respectively, reach point x; that is,
Differentiating Equation 20.3 with respect to x gives

or

To minimize the total treatment time, the optimal solution is to move the faster of the two leaves at the maximum allowed speed, Vmax, and modulate the intensity with the slower leaf. If the gradient of the profile dI(x)/dx is zero, then according to Equation 20.5, the two speeds are equal
and should be set to Vmax. If the gradient is positive, then the speed of leaf 2 is higher than that of leaf 1 and therefore it is set equal to Vmax; and if the gradient is negative, then the speed of leaf 1 is set equal to Vmax. Once the speed of the faster leaf is set to Vmax, the speed of the slower leaf can be uniquely determined from Equation 20.5; that is,
and should be set to Vmax. If the gradient is positive, then the speed of leaf 2 is higher than that of leaf 1 and therefore it is set equal to Vmax; and if the gradient is negative, then the speed of leaf 1 is set equal to Vmax. Once the speed of the faster leaf is set to Vmax, the speed of the slower leaf can be uniquely determined from Equation 20.5; that is,
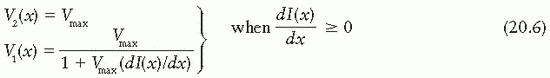
and
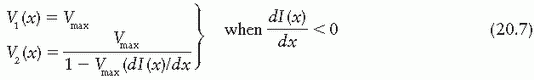
In summary, the DMLC algorithm is based on the following principles:
If the gradient of the intensity profile is positive (increasing fluence), the leading leaf should move at the maximum speed and the trailing leaf should provide the required intensity modulation.
If the spatial gradient of the intensity profile is negative (decreasing fluence), the trailing leaf should move at the maximum speed and the leading leaf should provide the required intensity modulation.
B. IMRT WITH ROTATING FAN BEAMS: TOMOTHERAPY
Tomotherapy is an IMRT technique in which the patient is treated slice by slice by IMBs in a manner analogous to CT imaging. A special collimator is designed to generate the IMBs as the gantry rotates around the longitudinal axis of the patient. In one device, the couch is indexed one to two slices at a time, and in the other, the couch moves continuously as in a helical CT. The former was developed by the NOMOS Corporation2 and the latter by the medical physics group at the University of Wisconsin.3
B.1. The Peacock System
The NOMOS collimator device is called the MIMiC and is used in conjunction with a TPS, PEACOCKPLAN. The MIMiC and the PEACOCKPLAN together are known as the PEACOCK system. Other important accessories include a special indexing table called the CRANE, a patient fixation device called the TALON, and an ultrasound-based target localization system called the BAT (all NOMOS products are named after birds).
MULTILEAF INTENSITY-MODULATING COLLIMATOR. The MIMiC collimator consists of a long transverse slit aperture provided with two banks of 20 leaves each (Fig. 20.5). Each leaf can be moved independently and can provide an opening (at isocenter) of either (1 cm × 1 cm) or (1 cm × 2 cm). Each bank can therefore treat 1- or 2-cm-thick slices of tissue 20 cm in diameter; because there are two such banks, a 2- or 4-cm slice of tissue can be treated at one time. For extending the length of treatment volume beyond 4 cm, the couch is moved to treat the adjacent slices. This gives rise to field junctions, which is of concern in MIMiC-based IMRT.
The MIMiC leaves are made of tungsten and are approximately 8 cm thick in the direction of the beam. The transmitted intensity through a leaf is approximately 1% for 10-MV x-rays. The leaf interfaces are multistepped to limit interleaf leakage to within 1%. Each leaf can be switched in 100 to 150 milliseconds, thus allowing a rapid change in beam apertures as the gantry rotates. Considering the number of possible field apertures at each gantry angle and the number of intensity steps that can be delivered at each gantry position, it is possible to create more than 1013 beam configurations for each arc (18). Thus, the intensity modulation of beams can be finely controlled by the MIMiC technology.
A potential problem with MIMiC-based IMRT is the possibility of mismatch between adjacent slice pairs needed to treat a long target volume. Carol et al. (19) have studied the problem and shown that perfectly matched slices gave rise to 2% to 3% dose inhomogeneity across the junction. However, even a 2-mm error in indexing the couch resulted in dose inhomogeneity of the order of 40%. NOMOS solved this problem by designing accurate table indexing and patient fixation devices.
CRANE. Because of the potential field-matching problems in the use of MIMiC for treating adjacent slice pairs along the length of the patient, it is imperative to move the couch with extreme accuracy. A special indexing table called the CRANE has been designed by NOMOS, which is capable of moving the couch longitudinally with a 300-lb weight to distances of 0.1 to 0.2 mm. With such accuracy, it is possible to reduce the junctional dose inhomogeneity to within ±3% (20).
TALON. Because of the stringent matchline requirements, NOMOS supplies an invasive head fixation system called the TALON. The device is attachable to the CT or the treatment unit couch and fixes the head position by the insertion of two bone screws into the inner table of the skull. Once the bone screws have been inserted, the TALON can be removed or reattached quickly as needed. An evacuated headrest can also be used to assist in repositioning at each treatment session.
For further details on the PEACOCK system of IMRT, the reader is referred to reference (19).
B.2. Helical Tomotherapy
Mackie et al. (20) proposed a method of IMRT delivery in which the linac head and gantry rotate while the patient is translated through the doughnut-shaped aperture in a manner analogous to a helical CT scanner. In this form of tomotherapy, the problem of interslice matchlines is minimized because of the continuous helical motion of the beam around the longitudinal axis of the patient.
A schematic diagram of the tomotherapy unit proposed by Mackie et al. is shown in Figure 20.6A and B. Figure 20.6C




Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree