Interaction of Radiation with Matter
This chapter introduces the concepts and principles that govern x- and γ-ray photon interactions with matter and the energetic electrons those interactions set into motion. It considers the fate of these electrons as they subsequently transfer and distribute their kinetic energy in the material they traverse. These electrons transfer their kinetic energy to the surrounding medium by interacting with surrounding atoms via excitation, ionization, and radiative emissions. The photon interactions to be discussed include Rayleigh and Compton scattering and photoelectric absorption. The metrics commonly used to describe the change in intensity and quality of x- and γ-rays by attenuation as they traverse matter are presented. Energy deposited from radiation per unit mass is the definition of the quantity Absorbed Dose. There are many “dose” terms used in medical imaging, radiation biology, and radiation protection, each with its own specific meaning and application. Unfortunately, absorbed dose and many other doserelated terms (including KERMA, Equivalent Dose, Imparted Energy, Effective Dose, and others) are often used incorrectly. The definitions of these terms, their intended applications, and related concepts are discussed below and throughout the book.
3.1 PARTICLE INTERACTIONS
Particles of ionizing radiation include charged particles, such as alpha particles (α+2), protons (p+), beta particles (β–), positrons (β+), and energetic extranuclear electrons (e–), and uncharged particles, such as neutrons. The behavior of heavy charged particles (e.g., alpha particles and protons) is different from that of lighter charged particles such as electrons and positrons.
3.1.1 Excitation, Ionization, and Radiative Losses
Energetic charged particles interact with matter by electrical (i.e., coulombic) forces and lose kinetic energy via excitation, ionization, and radiative losses. Excitation and ionization occur when charged particles lose energy by interacting with orbital electrons in the medium. These interactional, or collisional, losses occur due to the coulombic forces exerted on charged particles when they pass in proximity to the electric field generated by the atom’s electrons and protons. Excitation is the transfer of some of the incident particles’ energy to electrons in the absorbing material, promoting them to a different orbital with a higher energy level. The main difference between orbitals and energy levels is that orbitals show the most probable pathway of an electron that is in motion around the nucleus whereas energy levels show the relative locations of orbitals according to the amount of energy they possess. In excitation, the energy transferred to an electron does not exceed its binding energy. Following excitation, the electron will return to a lower energy level, with the emission of the excitation energy in the form of electromagnetic radiation or Auger electrons. This process is referred to as de-excitation (Fig. 3-1A). If the transferred energy exceeds
the binding energy of the electron, ionization occurs, whereby the electron is ejected from the atom (Fig. 3-1B). The result of ionization is an ion pair consisting of the ejected electron and the positively charged atom. Sometimes, the ejected electrons possess sufficient energy to produce further ionizations called secondary ionization. These electrons are called delta rays.
the binding energy of the electron, ionization occurs, whereby the electron is ejected from the atom (Fig. 3-1B). The result of ionization is an ion pair consisting of the ejected electron and the positively charged atom. Sometimes, the ejected electrons possess sufficient energy to produce further ionizations called secondary ionization. These electrons are called delta rays.
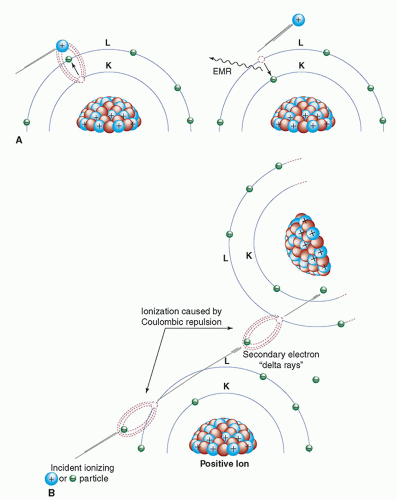 ▪ FIGURE 3-1 A. Excitation (left) and de-excitation (right) with the subsequent release of electromagnetic radiation. B. Ionization and the production of delta rays. |
Approximately 70% of the energy deposition of energetic electrons in soft tissue occurs via ionization. However, as electron energy decreases the probability of energy loss via excitation increases. For a very low energy electron (˜40 eV) the probabilities of excitation and ionization are equal and with further reductions in electron energy, the probability of ionization rapidly diminishes becoming zero (in tissue) below the
first ionization state of liquid water at approximately 11.2 eV. So, while the smallest binding energies for electrons in carbon, nitrogen, and oxygen are less than 10 eV, the average energy deposited per ion pair produced in air (mostly nitrogen and oxygen) and soft tissue (mostly hydrogen, carbon, and oxygen) is approximately 34 and 22 eV, respectively. The energy difference is the result of the excitation process. Medical imaging with x-rays and γ-rays results in the production of energetic electrons by mechanisms discussed later in this chapter. It should be appreciated that, owing to the relatively modest amount of energy necessary to produce a secondary electron, each of these energetic electrons will result in an abundance of secondary electrons as it deposit its energy in tissue. For example, a 10 keV electron will result in the production of over 450 secondary electrons, most with energies between 10 and 70 eV.
first ionization state of liquid water at approximately 11.2 eV. So, while the smallest binding energies for electrons in carbon, nitrogen, and oxygen are less than 10 eV, the average energy deposited per ion pair produced in air (mostly nitrogen and oxygen) and soft tissue (mostly hydrogen, carbon, and oxygen) is approximately 34 and 22 eV, respectively. The energy difference is the result of the excitation process. Medical imaging with x-rays and γ-rays results in the production of energetic electrons by mechanisms discussed later in this chapter. It should be appreciated that, owing to the relatively modest amount of energy necessary to produce a secondary electron, each of these energetic electrons will result in an abundance of secondary electrons as it deposit its energy in tissue. For example, a 10 keV electron will result in the production of over 450 secondary electrons, most with energies between 10 and 70 eV.
Specific Ionization
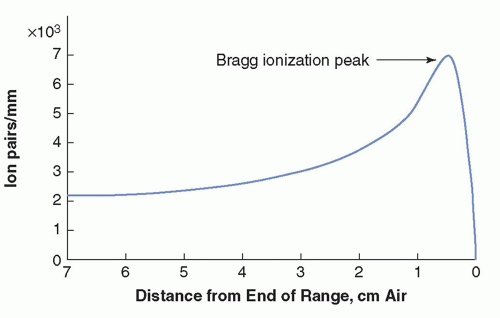
The average number of primary and secondary ion pairs produced per unit length of a charged particle’s path is called the specific ionization, expressed in ion pairs (IP)/mm. Specific ionization increases with the square of the electrical charge (Q) of the particle and decreases with the square of the incident particle velocity (v); thus, specific ionization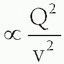 
. A larger charge produces a greater coulombic field; as the particle loses kinetic energy, it slows down, allowing the coulombic field to interact at a given location for a longer period of time. The kinetic energies of alpha particles emitted by naturally occurring radionuclides extend from a minimum of about 4.05 MeV (Th-232) to a maximum of about 10.53 MeV (Po-212). The ranges of alpha particles in matter are quite limited and, for the alpha particle energies mentioned above, their ranges in air are 2.49 and 11.6 cm, respectively. In tissue, the alpha particle range is reduced to less than the diameters of a dozen or so cells (˜30 to 130 µm). The specific ionization of an alpha particle can be as high as approximately 7,000 IP/mm in air and about 10 million IP/mm in soft tissue. The specific ionization as a function of the particle’s path is shown for a 7.69-MeV alpha particle from 214Po in air (Fig. 3-2). As the alpha particle slows, the specific ionization increases to a maximum (called the Bragg peak), beyond which it decreases rapidly as the alpha particle acquires electrons and becomes electrically neutral, thus losing its capacity for further ionization. The large Bragg peak associated with heavy charged particles produced by specialized accelerators is used at some medical facilities to provide this treatment in lieu of surgical excision or conventional radiation therapy. For example, there are about 30 proton centers currently in the United States, many more in the around the world as well as at least 8 carbon ion therapy centers. By adjusting the kinetic energy of heavy charged particles, a large radiation dose can be delivered at a
particular depth and over a fairly narrow range of tissue containing a lesion. On either side of the Bragg peak, the dose to tissue is substantially lower. Compared to heavy charged particles, the specific ionization of electrons is much lower (in the range of 5 to 10 IP/mm of air).
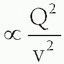. A larger charge produces a greater coulombic field; as the particle loses kinetic energy, it slows down, allowing the coulombic field to interact at a given location for a longer period of time. The kinetic energies of alpha particles emitted by naturally occurring radionuclides extend from a minimum of about 4.05 MeV (Th-232) to a maximum of about 10.53 MeV (Po-212). The ranges of alpha particles in matter are quite limited and, for the alpha particle energies mentioned above, their ranges in air are 2.49 and 11.6 cm, respectively. In tissue, the alpha particle range is reduced to less than the diameters of a dozen or so cells (˜30 to 130 µm). The specific ionization of an alpha particle can be as high as approximately 7,000 IP/mm in air and about 10 million IP/mm in soft tissue. The specific ionization as a function of the particle’s path is shown for a 7.69-MeV alpha particle from 214Po in air (Fig. 3-2). As the alpha particle slows, the specific ionization increases to a maximum (called the Bragg peak), beyond which it decreases rapidly as the alpha particle acquires electrons and becomes electrically neutral, thus losing its capacity for further ionization. The large Bragg peak associated with heavy charged particles produced by specialized accelerators is used at some medical facilities to provide this treatment in lieu of surgical excision or conventional radiation therapy. For example, there are about 30 proton centers currently in the United States, many more in the around the world as well as at least 8 carbon ion therapy centers. By adjusting the kinetic energy of heavy charged particles, a large radiation dose can be delivered at a particular depth and over a fairly narrow range of tissue containing a lesion. On either side of the Bragg peak, the dose to tissue is substantially lower. Compared to heavy charged particles, the specific ionization of electrons is much lower (in the range of 5 to 10 IP/mm of air).
 ▪ FIGURE 3-2 Specific ionization (ion pairs/mm) in air of a 7.69-MeV alpha particle from 214Po as a function of distance from the end of its range. The rapid increase in specific ionization reaches a maximum (Bragg peak) and then drops off sharply as the particle kinetic energy is exhausted and the charged particle is neutralized. |
Charged Particle Tracks
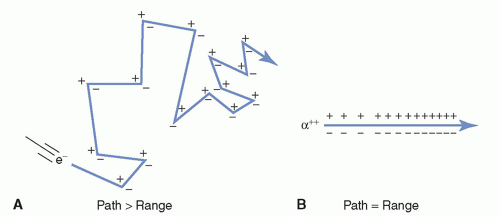
Another important distinction between heavy charged particles and electrons is their paths in matter. Electrons follow tortuous paths in matter as the result of multiple scattering events caused by coulombic deflections (repulsion and/or attraction). The sparse tortuous ionization track of an electron is illustrated in Figure 3-3A. On the other hand, the larger mass of a heavy charged particle results in a dense and usually linear ionization track (Fig. 3-3B). The path length of a particle is defined as the distance the particle travels. The range of a particle is defined as the depth of penetration of the particle in matter. As illustrated in Figure 3-3, the path length of the electron almost always exceeds its range, whereas the typically straight ionization track of a heavy charged particle results in the path length and range being nearly equal. Additional information on the pattern of energy deposition of charged particles at the cellular level and their radiobiological significance is presented in Chapter 20.
Linear Energy Transfer
While specific ionization reflects all energy losses that occur before an ion pair is produced, the linear energy transfer (LET) is a measure of the average amount of energy deposited locally (near the incident particle track) in the absorber per unit path length. LET is often expressed in units of keV or eV per µm. The LET of a charged particle is proportional to the square of the charge and inversely proportional to the particle’s kinetic energy (i.e., LET 
Q2/Ek). The LET of a particular type of radiation describes the local energy deposition density, which can have a substantial impact on the biologic consequences of radiation exposure. In general, for a given absorbed dose, the dense ionization tracks of “high LET” radiations (alpha particles, protons, etc.) deposit their energy over a much shorter range and are much more damaging to cells than the sparse ionization pattern associated with “low LET” radiations. Low LET radiation includes energetic electrons (e.g., β– and β+) and ionizing electromagnetic radiation (γ- and x-rays, whose interactions set electrons into motion). By way of perspective, the exposure of patients to diagnostic x-rays results in the production of energetic electrons with an average LET of approximately 3 keV/µm in soft tissue, whereas the average LET of 5-MeV alpha particles in soft tissue is approximately
100 keV/µm. Despite their typically much higher initial kinetic energies, the range of high LET radiation is much less than that of low LET radiation. For example at the point where an alpha particle and electron traversing tissue have the same kinetic energy, say 100 keV, their ranges from that point will be 1.4 and 200 µm, respectively.
Q2/Ek). The LET of a particular type of radiation describes the local energy deposition density, which can have a substantial impact on the biologic consequences of radiation exposure. In general, for a given absorbed dose, the dense ionization tracks of “high LET” radiations (alpha particles, protons, etc.) deposit their energy over a much shorter range and are much more damaging to cells than the sparse ionization pattern associated with “low LET” radiations. Low LET radiation includes energetic electrons (e.g., β– and β+) and ionizing electromagnetic radiation (γ- and x-rays, whose interactions set electrons into motion). By way of perspective, the exposure of patients to diagnostic x-rays results in the production of energetic electrons with an average LET of approximately 3 keV/µm in soft tissue, whereas the average LET of 5-MeV alpha particles in soft tissue is approximately 100 keV/µm. Despite their typically much higher initial kinetic energies, the range of high LET radiation is much less than that of low LET radiation. For example at the point where an alpha particle and electron traversing tissue have the same kinetic energy, say 100 keV, their ranges from that point will be 1.4 and 200 µm, respectively.
 ▪ FIGURE 3-3 A. Electron scattering results in the path length of the electron being greater than its range. B. Heavily charged particles, like alpha particles, produce a dense, nearly linear ionization track, resulting in the path and range being essentially equal. |
Scattering
Scattering refers to an interaction that deflects a particle or photon from its original trajectory. A scattering event in which the total kinetic energy of the colliding particles is unchanged is called elastic. Billiard ball collisions, for example, are elastic (disregarding frictional losses). When scattering occurs with a loss of kinetic energy (i.e., the total kinetic energy of the scattered particles is less than that of the particles before the interaction), the interaction is said to be inelastic. For example, the process of ionization can be considered an elastic interaction if the binding energy of the electron is negligible compared to the kinetic energy of the incident electron (i.e., the kinetic energy of the ejected electron is equal to the kinetic energy lost by the incident electron). If the binding energy that must be overcome to ionize the atom is not insignificant compared to the kinetic energy of the incident electron (i.e., the kinetic energy of the ejected electron is less than the kinetic energy lost by the incident electron), the process is said to be inelastic.
Radiative Interactions—Bremsstrahlung
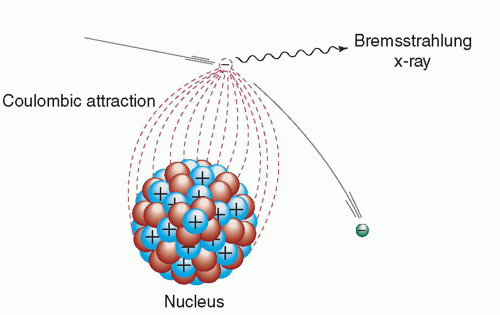
While most electron interactions with the atomic nuclei are elastic, electrons can undergo inelastic interactions in which the path of the electron is deflected by the positively charged nucleus, with a loss of kinetic energy. This energy is instantaneously emitted as electromagnetic radiation (i.e., x-rays). Energy is conserved, as the energy of the radiation is equal to the kinetic energy lost by the electron.
The radiation emission accompanying electron deceleration is called bremsstrahlung, a German word meaning “braking radiation” (Fig. 3-4). The deceleration of the high-speed electrons in an x-ray tube produces the bremsstrahlung x-rays used in diagnostic imaging.
Total bremsstrahlung emission per atom is proportional to Z2, where Z is the atomic number of the absorber, and inversely proportional to the square of the mass of the incident particle, that is, Z2/m2. Due to the strong influence of the particle’s mass, bremsstrahlung production by heavier charged particles such as protons and alpha particles will be less than one-millionth of that produced by electrons.
The energy of a bremsstrahlung x-ray photon can be any value up to and including the entire kinetic energy of the deflected electron. Thus, when many
electrons undergo bremsstrahlung interactions, the result is a continuous spectrum of x-ray energies. This radiative energy loss is responsible for the majority of the x-rays produced by x-ray tubes and is discussed in greater detail in Chapter 6.
electrons undergo bremsstrahlung interactions, the result is a continuous spectrum of x-ray energies. This radiative energy loss is responsible for the majority of the x-rays produced by x-ray tubes and is discussed in greater detail in Chapter 6.
 ▪ FIGURE 3-4 Radiative energy loss via bremsstrahlung (braking radiation). |
Positron Annihilation
The fate of positrons (β+) is unlike that of negatively charged electrons (e– and β–) that ultimately become bound to atoms. As mentioned above, all energetic electrons (positively and negatively charged) lose their kinetic energy by excitation, ionization, and radiative interactions. When a positron (a form of antimatter) reaches the end of its range, it interacts with a negatively charged electron, resulting in the annihilation of the electron-positron pair and the complete conversion of their rest mass to energy in the form of two oppositely directed 0.511-MeV annihilation photons. This process occurs following radionuclide decay by positron emission (see Chapter 15). Imaging of the distribution of positron-emitting radiopharmaceuticals in patients is accomplished by the detection of the annihilation photon pairs during positron emission tomography (PET) (see Chapter 19). The annihilation photons are not often emitted at exactly 180° apart because there is often a small amount of residual momentum in the positron when it interacts with the oppositely charged electron. This noncolinearity is not severe (˜0.5°), and its blurring effect in the typical PET imaging system is not clinically significant.
3.1.2 Neutron Interactions
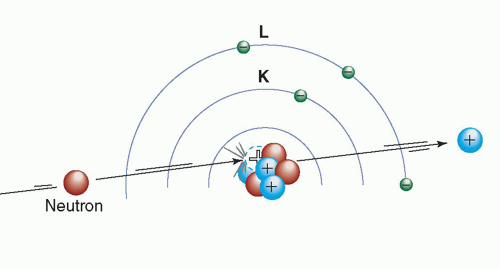
Unlike protons and electrons, neutrons, being uncharged particles, cannot cause excitation and ionization via coulombic interactions with orbital electrons. They can, however, interact with atomic nuclei, sometimes liberating charged particles or nuclear fragments that can directly cause excitation and ionization (Fig. 3-5). Neutrons often interact with atomic nuclei of light elements (e.g., H, C, O) by scattering in “billiard ball”-like collisions, producing recoil nuclei that lose their energy via excitation and ionization. In tissue, energetic neutrons interact primarily with the hydrogen in water, producing recoil protons (hydrogen nuclei). Neutrons may also be captured by atomic nuclei. Neutron capture results in a large energy release (typically 2 to 7 MeV) due to the large binding energy of the neutron. In some cases, one or more neutrons are reemitted; in other cases, the neutron is retained, converting the atom into a different isotope. For example, the capture of a neutron by a hydrogen atom (1H) results in deuterium (2H) and the emission of a 2.22-MeV γ-ray, reflecting the increase in the binding energy of the nucleus:
1H + 1n → 2H + γ γ-ray energy (Eγ) = 2.22 MeV.
Some nuclides produced by neutron absorption are stable, and others are radioactive (i.e., unstable). As discussed in Chapter 2, neutron absorption in some very
heavy nuclides such as 235U can cause nuclear fission, producing very energetic fission fragments, neutrons, and γ-rays. Neutron interactions important to the production of radiopharmaceuticals are described in greater detail in Chapter 16.
heavy nuclides such as 235U can cause nuclear fission, producing very energetic fission fragments, neutrons, and γ-rays. Neutron interactions important to the production of radiopharmaceuticals are described in greater detail in Chapter 16.
 ▪ FIGURE 3-5 Schematic example of collisional energy loss. An uncharged particle (neutron) interacts with the atomic nucleus of an atom resulting in the ejection of a proton. This interaction results in the transformation of the atom into a new element with an atomic number (Z) reduced by 1. |
3.2 X-RAY AND GAMMA (γ)-RAY INTERACTIONS
When traversing matter, photons will penetrate without interaction, scatter, or be absorbed. There are four major types of interactions of x-ray and γ-ray photons with matter, the first three of which play a role in diagnostic radiology and nuclear medicine: (1) Rayleigh scattering, (2) Compton scattering, (3) photoelectric absorption, and (4) pair production.
3.2.1 Rayleigh Scattering
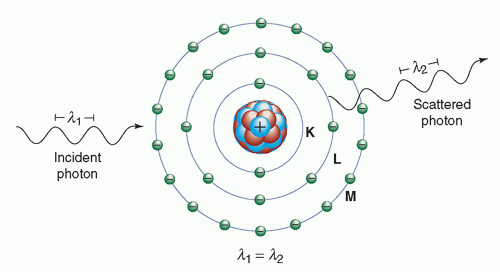
In Rayleigh scattering, the incident photon interacts with and excites the total atom, as opposed to individual electrons as in Compton scattering or the photoelectric effect (discussed later). This interaction occurs mainly with very low energy x-rays, such as those used in mammography (15 to 30 keV). During the Rayleigh scattering event, the electric field of the incident photon’s electromagnetic wave expends energy, causing all of the electrons in the scattering atom to oscillate in phase. The atom’s electron cloud immediately radiates this energy, emitting a photon of the same energy but in a slightly different direction (Fig. 3-6). In this interaction, electrons are not ejected, and thus, ionization does not occur. In general, the average scattering angle decreases as the x-ray energy increases. In medical imaging, detection of the scattered x-ray will have a deleterious effect on image quality. However, this type of interaction has a low probability of occurrence in the diagnostic energy range. In soft tissue, Rayleigh scattering accounts for less than 5% of x-ray interactions above 70 keV and at most only accounts for about 10% of interactions at 30 keV. Rayleigh interactions are also referred to as “coherent” or “classical” scattering.
3.2.2 Compton Scattering
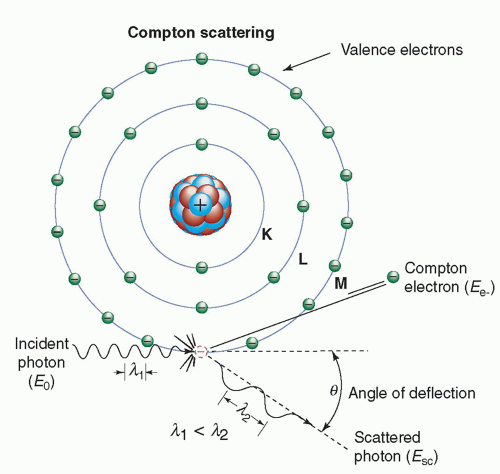
Compton scattering (also called inelastic or nonclassical scattering) is the predominant interaction of x-ray and γ-ray photons in the diagnostic energy range with soft
tissue. In fact, Compton scattering not only predominates in the diagnostic energy range above 26 keV in soft tissue but also continues to predominate well beyond diagnostic energies to approximately 30 MeV. This interaction is most likely to occur between photons and outer (“valence”)-shell electrons (Fig. 3-7). The electron is ejected from the atom, and the scattered photon is emitted with some reduction in energy relative to the incident photon. As with all types of interactions, both energy and momentum must be conserved. Thus, the energy of the incident photon (Eo) is equal to the sum of the energy of the scattered photon (Esc) and the kinetic energy of the ejected electron (Ee-), as shown in Equation 3-1. The binding energy of the electron that was ejected is comparatively small and can be ignored.
tissue. In fact, Compton scattering not only predominates in the diagnostic energy range above 26 keV in soft tissue but also continues to predominate well beyond diagnostic energies to approximately 30 MeV. This interaction is most likely to occur between photons and outer (“valence”)-shell electrons (Fig. 3-7). The electron is ejected from the atom, and the scattered photon is emitted with some reduction in energy relative to the incident photon. As with all types of interactions, both energy and momentum must be conserved. Thus, the energy of the incident photon (Eo) is equal to the sum of the energy of the scattered photon (Esc) and the kinetic energy of the ejected electron (Ee-), as shown in Equation 3-1. The binding energy of the electron that was ejected is comparatively small and can be ignored.
 ▪ FIGURE 3-6 Rayleigh scattering. The diagram shows that the incident photon λ1, interacts with an atom and the scattered photon λ2 is being emitted with the same wavelength and energy. Rayleigh scattered photons are typically emitted in the forward direction fairly close to the trajectory of the incident photon. K, L, and M are electron shells. |
Compton scattering results in the ionization of the atom and a division of the incident photon’s energy between the scattered photon and the ejected electron. The ejected electron will lose its kinetic energy via excitation and ionization of atoms in the surrounding material. The Compton scattered photon may traverse the medium without interaction or may undergo subsequent interactions such as Compton scattering, photoelectric absorption (to be discussed shortly), or Rayleigh scattering.
The energy of the scattered photon can be calculated from the energy of the incident photon and the angle (with respect to the incident trajectory) of the scattered photon:
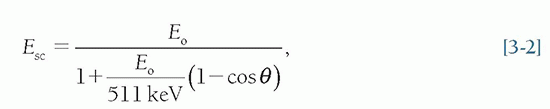
where Esc = the energy of the scattered photon, Eo = the incident photon energy, and θ = the angle of the scattered photon.
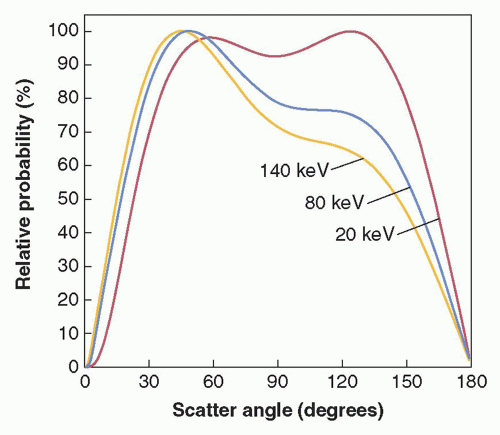
As the incident photon energy increases, both scattered photons and electrons are scattered more toward the forward direction (Fig. 3-8). In x-ray transmission imaging, these photons are much more likely to be detected by the image receptor.
In addition, for a given scattering angle, the fraction of energy transferred to the scattered photon decreases with increasing incident photon energy. Thus, for higher energy incident photons, the majority of the energy is transferred to the scattered electron. For example, for a 60° scattering angle, the scattered photon energy (Esc) is 90% of the incident photon energy (Eo) at 100 keV but only 17% at 5 MeV. When Compton scattering occurs at the lower x-ray energies used in diagnostic imaging (15 to 150 keV), the majority of the incident photon energy is transferred to the scattered photon. For example, following the Compton interaction of an 80-keV photon, the minimum energy of the scattered photon is 61 keV. Thus, even with maximal energy loss, the scattered photons have relatively high energies and tissue penetrability. In x-ray transmission imaging and nuclear emission imaging, the detection of scattered photons by the image receptors results in a degradation of image contrast and an increase in random noise. These concepts, and many others related to image quality, will be discussed in Chapter 4.
In addition, for a given scattering angle, the fraction of energy transferred to the scattered photon decreases with increasing incident photon energy. Thus, for higher energy incident photons, the majority of the energy is transferred to the scattered electron. For example, for a 60° scattering angle, the scattered photon energy (Esc) is 90% of the incident photon energy (Eo) at 100 keV but only 17% at 5 MeV. When Compton scattering occurs at the lower x-ray energies used in diagnostic imaging (15 to 150 keV), the majority of the incident photon energy is transferred to the scattered photon. For example, following the Compton interaction of an 80-keV photon, the minimum energy of the scattered photon is 61 keV. Thus, even with maximal energy loss, the scattered photons have relatively high energies and tissue penetrability. In x-ray transmission imaging and nuclear emission imaging, the detection of scattered photons by the image receptors results in a degradation of image contrast and an increase in random noise. These concepts, and many others related to image quality, will be discussed in Chapter 4.
 ▪ FIGURE 3-7 Compton scattering. The diagram shows the incident photon with energy Eo, interacting with a valence-shell electron that results in the ejection of the Compton electron (Ee) and the simultaneous emission of a Compton scattered photon Esc emerging at an angle θ relative to the trajectory of the incident photon. K, L, and M are electron shells. |
 ▪ FIGURE 3-8 Graph illustrates relative Compton scatter probability as a function of scattering angle for 20-, 80-, and 140-keV photons in tissue. Each curve is normalized to 100%. (Courtesy of John M. Boone, PhD, Department of Radiology, School of Medicine, University of California, Davis.) |
The laws of conservation of energy and momentum place limits on both scattering angle and energy transfer. For example, the maximal energy transfer to the Compton electron (and thus, the maximum reduction in photon energy) occurs with a 180° photon scatter (backscatter). In fact, the maximal energy of the scattered photon is limited to 511 keV at 90° scattering and 255 keV for a 180° scattering event. These limits on scattered photon energy hold even for extremely high-energy photons (e.g., therapeutic energy range). The scattering angle of the ejected electron cannot exceed 90°, whereas that of the scattered photon can be any value including a 180° backscatter. In contrast to the scattered photon, the energy of the ejected electron is usually absorbed near the scattering site.
The incident photon energy must be substantially greater than the electron’s binding energy before a Compton interaction is likely to take place. Thus, the relative probability of a Compton interaction increases, compared to Rayleigh scattering or photoelectric absorption, as the incident photon energy increases. The probability of Compton interaction also depends on the electron density (number of electrons/g × density). Except for hydrogen, the total number of electrons/g is fairly constant in tissue; thus, the probability of Compton scattering per unit mass is nearly independent of Z, and the probability of Compton scattering per unit volume is approximately proportional to the density of the material. Compared to other elements, the absence of neutrons in the hydrogen atom results in an approximate doubling of electron density. Thus, hydrogenous materials have a higher probability of Compton scattering than anhydrogenous material of equal mass.
3.2.3 The Photoelectric Effect
In the photoelectric effect, all of the incident photon energy is transferred to an electron, which is ejected from the atom. The kinetic energy of the ejected photoelectron (Epe) is equal to the incident photon energy (Eo) minus the binding energy of the orbital electron (Eb) (Fig. 3-9, left).
In order for photoelectric absorption to occur, the incident photon energy must be greater than or equal to the binding energy of the electron that is ejected. A table of electron binding energies and other data important to medical imaging for elements 1-100 is listed in Appendix C. The ejected electron is most likely one whose binding energy is closest to, but less than, the incident photon energy. For example, for photons whose energies exceed the K-shell binding energy, photoelectric interactions with K-shell electrons are most probable. Following a photoelectric interaction, the atom is ionized, with an inner-shell electron vacancy. This vacancy will be filled by an electron from a shell with lower binding energy. This creates another vacancy, which, in turn, is filled by an electron from an even lower binding energy shell. Thus, an electron cascade from outer to inner shells occurs. The difference in binding energy is released as either characteristic x-rays or Auger electrons (see Chapter 2). The probability of characteristic x-ray emission decreases as the atomic number of the absorber decreases, and thus, characteristic x-ray emission does not occur frequently for diagnostic energy photon interactions in soft tissue. The photoelectric effect can and does occur with valence shell electrons such as when light photons strike the high Z materials that comprise the photocathode (e.g., cesium, rubidium, and antimony) of a photomultiplier tube. These materials are specially selected to provide weakly bound electrons (i.e., electrons with a low work function), so when illuminated the photocathode readily releases electrons (see Chapter 17). In this case, no inner shell electron cascade occurs and thus no characteristic x-rays are produced.
 ▪ FIGURE 3-9 Photoelectric absorption. Left: The diagram shows that a 100-keV photon is undergoing photoelectric absorption with an iodine atom. A. In this case, the K-shell electron is ejected with a kinetic energy equal to the difference between the incident photon energy and the K-shell binding energy (100 keV – 33 keV = 67 keV). B. The vacancy created in the K shell results in the transition of an electron from the L shell to the K shell. The difference in their binding energies (i.e., 33 keV – 5 keV) results in a 28-keV Kα characteristic x-ray. This electron cascade will continue, resulting in the production of other characteristic x-rays of lower energies. Note that the sum of the characteristic x-ray energies equals the binding energy of the ejected photoelectron (33 keV). C. An alternative (competing) process that can occur is the transfer of the difference in binding energy (transition energy), that would otherwise have been emitted as a characteristic x-ray (in this case the 28 keV) to an electron in the same atom whose binding energy is less than the transition energy. The figure shows the 28-keV Kα transition energy being transferred to an “M” shell electron that is ejected from the atom as an Auger electron with a kinetic energy equal to the transition energy minus its binding energy (28 keV – 1 keV = 27 keV). The probability of Auger electron emission increases relative to characteristic x-ray emission as the transition energy decreases. |
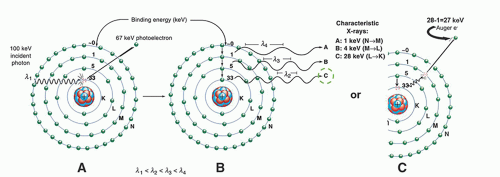
EXAMPLE: The K– and L-shell electron binding energies of iodine are 33 and 5 keV, respectively. If a 100-keV photon is absorbed by a K-shell electron in a photoelectric interaction, the photoelectron is ejected with a kinetic energy equal to Eo – Eb = 100 – 33 = 67 keV. A characteristic x-ray or Auger electron is emitted as an outer-shell electron fills the K-shell vacancy (e.g., L to K transition is 33 – 5 = 28 keV). The remaining energy is released by subsequent cascading events in the outer shells of the atom (i.e., M to L and N to M transitions). Note that the total of all the characteristic x-ray emissions in this example equals the binding energy of the K-shell photoelectron (Fig. 3-9, right).
Thus, photoelectric absorption results in the production of
A photoelectron
A positive ion (ionized atom)
Characteristic x-rays or Auger electrons
The probability of photoelectric absorption per unit mass is approximately proportional to Z3/E3, where Z is the atomic number, and E is the energy of the incident photon. For example, the photoelectric interaction probability in iodine (Z = 53) is (53/20)3 or 18.6 times greater than in calcium (Z = 20) for a photon of a particular energy.
The benefit of photoelectric absorption in x-ray transmission imaging is that there are no scattered photons to degrade the image. The fact that the probability of photoelectric interaction is proportional to 1/E3 explains, in part, why image contrast decreases when higher x-ray energies are used in the imaging process (see Chapters 4 and 7). If the photon energies are doubled, the probability of photoelectric interaction is decreased eightfold: (½)3 = 1/8.
Although the probability of the photoelectric effect decreases, in general, with increasing photon energy, there are exceptions. For every element, the probability of the photoelectric effect, as a function of photon energy, exhibits sharp discontinuities called absorption edges (see Fig. 3-10). The probability of interaction for photons of energy just above an absorption edge is much greater than that of photons of energy slightly below the edge. For example, a 33.2-keV x-ray photon is about six times as likely to have a photoelectric interaction with an iodine atom as a 33.1-keV photon.
As mentioned above, a photon cannot undergo a photoelectric interaction with an electron in a particular atomic shell or subshell if the photon’s energy is less than the binding energy of that shell or subshell. This causes a dramatic decrease in the probability of photoelectric absorption for photons whose energies are just below the
binding energy of a shell. Thus, the photon energy corresponding to an absorption edge is the binding energy of the electrons in that particular shell or subshell. An absorption edge is designated by a letter, representing the atomic shell of the electrons, followed by a roman numeral subscript denoting the subshell (e.g., K, LI, LII, LIII). The photon energy corresponding to a particular absorption edge increases with the atomic number (Z) of the element. For example, the primary elements comprising soft tissue (H, C, N, and O) have absorption edges below 1 keV. The element iodine (Z = 53), commonly used in radiographic contrast agents to provide enhanced x-ray attenuation, has a K-absorption edge of 33.2 keV (Fig. 3-10). The K-edge energy of the target material in most x-ray tubes (tungsten, Z = 74) is 69.5 keV. The K- and L-shell binding energies for elements with atomic numbers 1 to 100 are provided in Appendix C, Table C-3.
binding energy of a shell. Thus, the photon energy corresponding to an absorption edge is the binding energy of the electrons in that particular shell or subshell. An absorption edge is designated by a letter, representing the atomic shell of the electrons, followed by a roman numeral subscript denoting the subshell (e.g., K, LI, LII, LIII). The photon energy corresponding to a particular absorption edge increases with the atomic number (Z) of the element. For example, the primary elements comprising soft tissue (H, C, N, and O) have absorption edges below 1 keV. The element iodine (Z = 53), commonly used in radiographic contrast agents to provide enhanced x-ray attenuation, has a K-absorption edge of 33.2 keV (Fig. 3-10). The K-edge energy of the target material in most x-ray tubes (tungsten, Z = 74) is 69.5 keV. The K- and L-shell binding energies for elements with atomic numbers 1 to 100 are provided in Appendix C, Table C-3.
Related posts:
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
