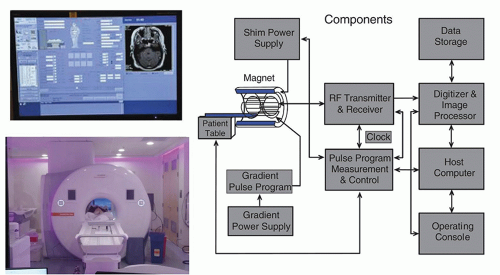
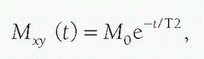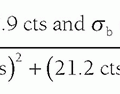The MR system is composed of several components including a magnet, magnetic field gradient coil, and radiofrequency (RF) coils, orchestrated by many processors and control subsystems, as shown in
Figure 12-5. Details of the individual components, methods of acquiring the MR signals, and reconstruction of images are described in the following sections.
12.2.1 Magnets
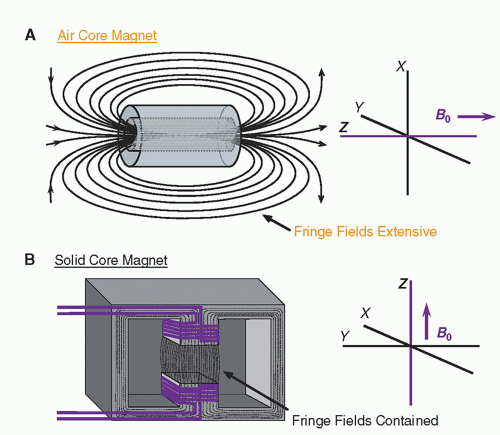
The magnet is the heart of the MR system. For any magnet type, performance criteria include field strength, temporal stability, and field homogeneity. These parameters are affected by the magnet design. Air core magnets are made of wire-wrapped cylinders of approximately 1-m diameter and greater, over a cylindrical length of 2 to 3 m, where the magnetic field is produced by an electric current in the wires. When the wires are energized, the magnetic field produced is parallel to the long axis of the cylinder. In most clinically designed systems, the magnetic field is horizontal and runs along the cranial-caudal axis of the patient lying supine (
Fig. 12-6A). Solid core magnets are constructed from permanent magnets, a wire-wrapped iron core “electromagnet,” or a hybrid combination. In these solid core designs, the magnetic field runs between the poles of the magnet, most often in a vertical direction (
Fig. 12-6B). Magnetic fringe fields extend well beyond the volume of the cylinder in air core designs. Fringe fields are a potential hazard and are discussed further in
Chapter 13.
To achieve a high magnetic field strength (greater than 1 T) requires the electromagnet core wires to be superconductive. Superconductivity is a characteristic of certain metals (
e.g., niobium-titanium alloys) that when maintained at extremely low temperatures (liquid helium; less than 4 K) exhibit no resistance to electric current. Superconductivity allows the closed-circuit electromagnet to be energized and
ramped up to the desired current and magnetic field strength by an external electric source. Replenishment of the liquid helium must occur continuously, because if the temperature rises above a critical value, the loss of superconductivity will occur and resistance heating of the wires will boil the helium, resulting in a “quench.” Superconductive magnets with field strengths of 1.5 to 3 T are common for clinical systems.
12.2.2 Magnetic Field Gradients
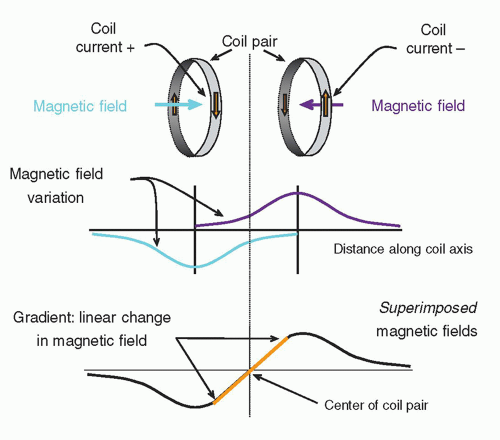
A magnetic field gradient is obtained by superimposing the magnetic fields of two or more coils carrying a direct current of specific amplitude and direction with a precisely defined geometry (
Fig. 12-7). The bipolar gradient field varies over a predefined field of view (FOV), and when superimposed upon
B0, a small, continuous variation in the field strength occurs from the center to the periphery with distance from the center point (the “null”). Interacting with the much, much stronger main magnetic field, the subtle linear variations are on the order of 0.004 T/m (4 mT/m) and are essential for localizing signals generated during the operation of the MR system.
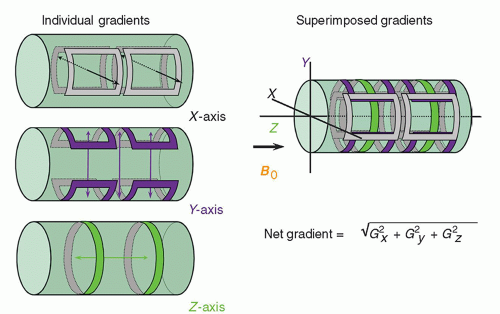
Inside the magnet bore, three sets of gradients reside along the logical coordinate axes—
x,
y, and
z—and produce a magnetic field variation determined by the magnitude of the applied current in each coil set (
Fig. 12-8). When independently energized, the three coils (
x,
y,
z) can produce a linearly variable magnetic field in any arbitrary direction, where the net gradient is equal to

. Gradient polarity reversals (positive to negative and negative to positive changes in magnetic field strength) are achieved by reversing the current direction in the gradient coils. Two important properties of magnetic gradients are as follows: (1) The
gradient field strength is determined by its peak amplitude and slope (change over distance), and typically ranges from 1 to 50 mT/m. (2) The
slew rate is the time to achieve the peak magnetic field amplitude. Typical slew rates of gradient fields are from 5 to 250 mT/m/ms. As the gradient field is turned on,
eddy currents are induced in nearby conductors such as adjacent RF coils and the patient, which produce magnetic fields that oppose the gradient field and limit the achievable slew rate. Actively shielded gradient coils and compensation circuits can reduce problems caused by eddy currents.
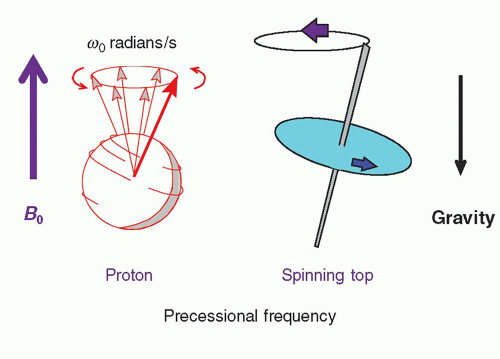
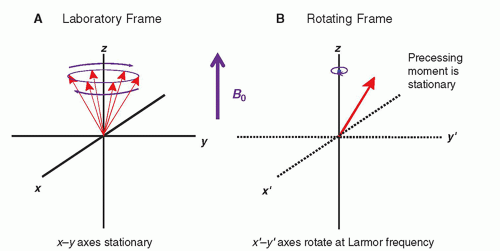
In a gradient magnetic field, protons maintain precessional frequencies corresponding to local magnetic field strength. At the middle of the gradient, called the gradient isocenter, there is no change in the field strength or precessional frequency. With a linear gradient, the magnetic field increases and decreases linearly in addition to the static magnetic field, as does the precessional frequency. The angular precessional frequency at a location within a linear gradient, ω, is
ω=γ(B0 + Gnet · d),
where Gnet is the net gradient and d is the distance from the gradient isocenter.
EXAMPLE: What is the precession frequency of proton placed 20 cm from the gradient isocenter if the net gradient is 2 G/cm and the field strength is 1.5 T?
The B0 field strength is 1.5 T and the gradient adds a magnetic field of 40 G or 0.004 T (2 G/cm × 20 cm). The effective magnetic field strength at the location is 1.504 T. The Larmor frequency of proton at 1.504 T is 64.04 MHz (42.58 × 1.504). The Larmor frequency of proton increases by 0.17 MHz due to the gradient field.
12.2.3 Radiofrequency Coils
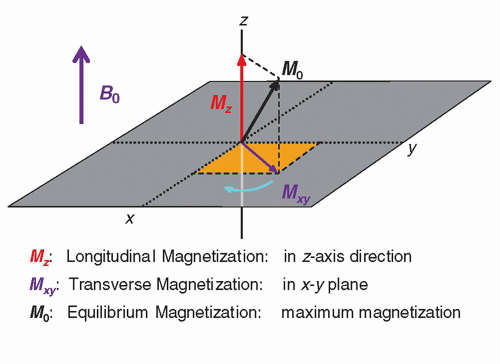
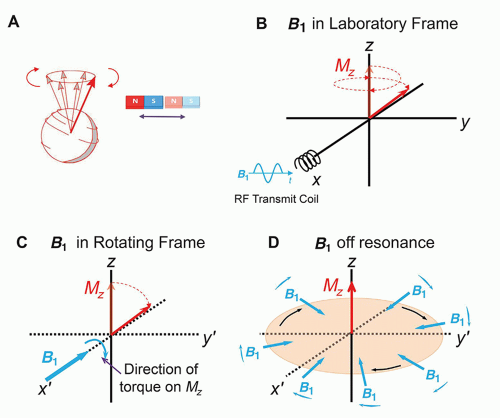
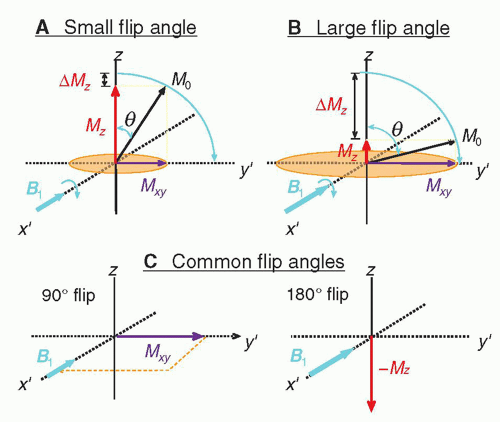
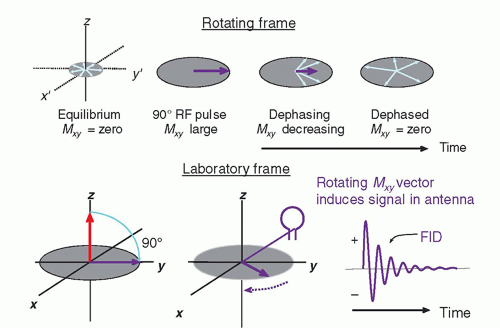
RF transmitter coils create an oscillating secondary magnetic field formed by passing an alternating current through a loop of wire. Irradiating the sample with an electromagnetic RF energy pulse tuned to the Larmor frequency induces the resonance of the magnetization within the sample. The magnetization along the direction of the static magnetic field, B0, shrinks with a simultaneous phase coherence that creates a perpendicular magnetization rotating at the Larmor frequency. This phenomenon is called excitation. To accomplish excitation and resonance, the created secondary field, called B1, must be arranged at right angles to the main magnetic field, B0. In an air core design with a horizontal field, the RF coil secondary field should be in the transverse or vertical axes, as the B1 field is created perpendicular to the transmit coils themselves. RF transmitter coils are therefore oriented above, below, or at the sides of the patient, and are usually cylindrical. In most systems, the body coil contained within the bore of the magnet is most frequently used, but also transmitter coils for the head, extremity, and some breast coils are coupled to a receiver coil.
The transverse magnetization within the sample returns to equilibrium conditions and releases detectable RF energy at the same frequency. While in phase coherence, the rotating magnetization vector generates a signal that is detected by highly sensitive antennas (RF receiver coils) to capture the basic MR signal. All RF receiver coils must resonate and efficiently store energy at the Larmor frequency. This is determined by the inductance and capacitance properties of the coil. RF transmit and receive coils need to be tuned prior to each acquisition and matched to accommodate the different magnetic inductance of each patient. Receiver coils must be properly placed to adequately detect the MR signal.
Very often, transmit and receive functions are separated to handle the variety of imaging situations that arise, and to maximize the SNR for an imaging sequence. Proximity RF coils include volume or bird-cage coils, the design of choice for brain imaging, the single-turn solenoid for imaging the extremities and the breasts, and the saddle coil. These coils are typically operated as both a transmitter and receiver of RF energy (
Fig. 12-9A).
Volume coils encompass the total area of the anatomy of interest and yield uniform excitation and SNR over the entire imaging volume. However, because of their relatively large size, images are produced with lower SNR than other types of coils. Enhanced performance is obtained with a process known as quadrature excitation and detection, which enables the energy to be transmitted and the signals to be received by two pairs of coils oriented at right angles, either electronically or physically. This detector manages two simultaneous channels known as the real (records MR information in phase with a reference signal) and the imaginary (records MR information 90° out of phase with the reference signal) channels, and increases
the SNR up to a factor of
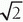
. If imbalances in the offset or gain of these detectors occur, then artifacts will be manifested, such as a “center point” artifact.
Phased array coils consisting of multiple coils and receivers are made of several overlapping loops, which extend the imaging FOV in one direction (
Fig. 12-9B-D). The small FOV of each individual coil provides excellent SNR and resolution, and each is combined to produce a composite image with the advantages of the local surface coil, so that all data can be acquired in a single sequence. Phased array coils for the spine, pelvis, breast, cardiac, and temporomandibular joint applications are commonly purchased with an MR system for optimal image quality.
Surface coils are used to achieve high SNR and high resolution when imaging anatomy near the surface of the patient. They are typically receive-only designs and are usually small and shaped for a specific imaging exam and for patient comfort. The received signal sensitivity, however, is limited to the volume located around the coil at a depth into the patient equal to the radius of the coil, which causes a loss of signal with depth. There are now intracavitary coils for endorectal, endovascular, endovaginal, esophageal, and urethral local imaging, and they can be used to receive signals from deep within the patient. In general, a body coil is used to transmit the RF energy and the local coil is used to receive the MR signal.
12.2.4 MR System Subcomponents
The control interfaces, RF source, detector, and amplifier, analog to digital converter (digitizer), pulse programmer, computer system, gradient power supplies, and image display are crucial components of the MR system. They integrate and synchronize the tasks necessary to produce the MR image (
Fig. 12-5).
The operator interface and computer systems vary with the manufacturer, but most consist of a computer system, dedicated processor for Fourier transformation, image processor to form the image, disk drives for storage of raw data and pulse sequence parameters, and a power distribution system to distribute and filter the direct and alternating current. The operator’s console is located outside of the scan room and provides the interface to the hardware and software for data acquisition (DAQ).
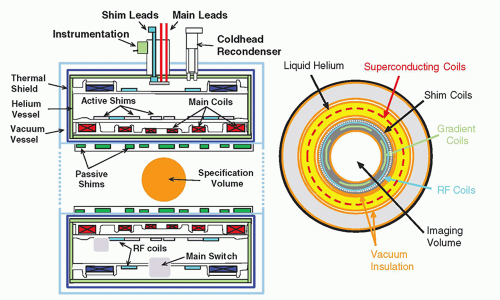
A cross section of the internal superconducting magnet components shows integral parts of the magnet system including the wire coils and cryogenic liquid containment vessel (
Fig. 12-10). In addition to the main magnet system, other components are also necessary. Shim coils interact with the main magnetic field to improve homogeneity (minimal variation of the magnetic flux density) over the volume used for patient imaging. RF coils exist within the main bore of the magnet to transmit energy to the patient as well as to receive returning signals. Gradient coils are contained within the main bore to produce a linear variation of magnetic field strength across the useful magnet volume.
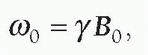
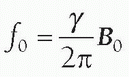
 . Gradient polarity reversals (positive to negative and negative to positive changes in magnetic field strength) are achieved by reversing the current direction in the gradient coils. Two important properties of magnetic gradients are as follows: (1) The gradient field strength is determined by its peak amplitude and slope (change over distance), and typically ranges from 1 to 50 mT/m. (2) The slew rate is the time to achieve the peak magnetic field amplitude. Typical slew rates of gradient fields are from 5 to 250 mT/m/ms. As the gradient field is turned on, eddy currents are induced in nearby conductors such as adjacent RF coils and the patient, which produce magnetic fields that oppose the gradient field and limit the achievable slew rate. Actively shielded gradient coils and compensation circuits can reduce problems caused by eddy currents.
. Gradient polarity reversals (positive to negative and negative to positive changes in magnetic field strength) are achieved by reversing the current direction in the gradient coils. Two important properties of magnetic gradients are as follows: (1) The gradient field strength is determined by its peak amplitude and slope (change over distance), and typically ranges from 1 to 50 mT/m. (2) The slew rate is the time to achieve the peak magnetic field amplitude. Typical slew rates of gradient fields are from 5 to 250 mT/m/ms. As the gradient field is turned on, eddy currents are induced in nearby conductors such as adjacent RF coils and the patient, which produce magnetic fields that oppose the gradient field and limit the achievable slew rate. Actively shielded gradient coils and compensation circuits can reduce problems caused by eddy currents.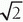 . If imbalances in the offset or gain of these detectors occur, then artifacts will be manifested, such as a “center point” artifact.
. If imbalances in the offset or gain of these detectors occur, then artifacts will be manifested, such as a “center point” artifact.