Fig. 1
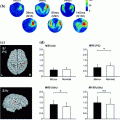
a Schematic showing the physical mechanisms of volume conduction for EEG and MEG. b Sensor space representation of left and right motor cortex envelope correlation. Seed sensor selected over right motor cortex
Sensor space measurement of connectivity is further complicated by interference measured at multiple sensors. MEG is susceptible to many sources of interference including external environmental noise sources such as computers or 50/60 Hz mains frequency interference as well as biological interference from, for example, the heart or muscles. If such interference sources impact on multiple MEG sensors, then this is likely to generate a spurious increase in sensor space connectivity values. An example (Brookes et al. 2011a) of this is given in Fig. 2: Fig. 2a, shows the measured electrocardiogram (ECG) from a single subject plotted alongside the MEG signal from a single sensor; Fig. 2b shows the spatial topography of Pearson correlation between the frequency filtered ECG and the frequency filtered sensor space MEG signals. Note not only the large (>0.5) correlation between MEG and ECG measurements, but also that the cardiac interference affects a large number of MEG sensors and unless adequately dealt with this could lead to spurious connectivity measurement, particularly when using sensor space measurement.
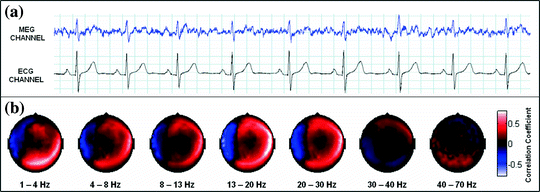

Fig. 2
Cardiac interference in sensor space. a The measured ECG and the magnetic field from a single MEG sensor. b The sensor space topography of cardiac interference plotted for each frequency band of interest adapted from Brookes et al. (2011a)
2.2 Projection to Brain Space and Source Leakage
The most useful mechanism to limit confounds associated with field spread is source space projection (Schoffelen and Gross 2009); this means reconstructing timecourses of electrical activity at a set of locations (voxels) in brain space via projection of the MEG/EEG field measurements. The spatial accuracy of such projections is limited since the reconstruction problem (the inverse problem) is mathematically ill-posed; field cancellation means that a single field pattern could result from an infinite number of different current density distributions and so no unique solution exists. However, a rich literature on source space reconstruction shows that, using specific assumption sets, reconstruction is possible with reasonable accuracy (5–8 mm) (Brookes et al. 2010). Figure 3 shows the principal advantage of applying source space projection to MEG data. The left hand panel shows inter-hemispheric functional connectivity measured in sensor space (equivalent to that shown in Fig. 1b) whilst the right hand panel shows interhemispheric connectivity, measured using the same data, in source space. Here projection from sensor to source space has been achieved via application of a beamformer spatial filtering approach (Gross et al. 2001; Robinson and Vrba 1998; Sekihara et al. 2006, 2001; van Veen et al. 1997) and the image shows functional connectivity, measured using correlation between band limited power envelopes (Brookes et al. 2011a), between a seed voxel (at the cross hairs) and all other locations in the brain. Note that unlike its sensor space equivalent, source space connectivity measurement facilitates direct interpretation of the image with respect to anatomy. In this example, functional connectivity in the resting state between the left and right sensorimotor areas is shown.


Fig. 3
The effect of projecting MEG data from sensor space to source space of functional connectivity measurement
In addition to the advantages summarised by Fig. 3, source space projection offers a second, less obvious advantage over sensor space measurement, specifically a marked improvement in signal to noise ratio. In projecting data from sensor to source space, an estimate of electrical source strength 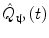 , is made at time t and at a predetermined location and orientation in the brain (ψ) using a weighted sum of MEG sensor measurements:
, is made at time t and at a predetermined location and orientation in the brain (ψ) using a weighted sum of MEG sensor measurements:
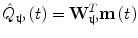
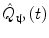 , is made at time t and at a predetermined location and orientation in the brain (ψ) using a weighted sum of MEG sensor measurements:
, is made at time t and at a predetermined location and orientation in the brain (ψ) using a weighted sum of MEG sensor measurements: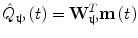
(1)
Here, m(t) is a (Nsens × 1) vector of magnetic field measurements made at time t, and W ψ is a (Nsens × 1) vector of weighting parameters tuned to a specific source space location and current orientation (Nsens represents the number of MEG sensors). Superscript T indicates a matrix transpose. Mathematically speaking, most of the commonly used MEG inverse solutions can be formulated in this way, and importantly the weighting parameters can be tuned not only to maintain signals originating at ψ, but also to suppress any unwanted interference signals. A good example of such an algorithm is beamforming (Gross et al. 2001; Robinson and Vrba 1998; Sekihara et al. 2006, 2001; van Veen et al. 1997), in which the weighting parameters (W ψ ) are derived based on power minimisation: the overall power in 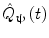 is minimised with a linear constraint that power originating from location/orientation
is minimised with a linear constraint that power originating from location/orientation 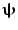 remains. Mathematically:
remains. Mathematically:
![$$ \min_{{{\mathbf{W}}_{{\varvec{\uppsi}}} }} \left[ {\varepsilon \left( {\hat{Q}_{{\varvec{\uppsi}}}^{2} } \right)} \right]\quad subject\;to\quad {\mathbf{W}}_{{\varvec{\uppsi}}}^{T} {\mathbf{L}}_{{\varvec{\uppsi}}} = 1 $$](/wp-content/uploads/2016/04/A272390_1_En_16_Chapter_Equ2.gif)
where L ψ is the lead field vector (containing the magnetic fields that would be measured at each of the MEG sensors in response to a dipole source of unit amplitude with location and orientation 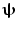 ). Note that the minimisation term ensures that any signal variance not originating from
). Note that the minimisation term ensures that any signal variance not originating from 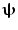 is minimised. An analytical solution to this problem is:
is minimised. An analytical solution to this problem is:
![$$ {\mathbf{W}}_{{\varvec{\uppsi}}}^{T} = \left[ {{\mathbf{L}}_{{\varvec{\uppsi}}}^{T} \left\{ {{\mathbf{C}} + \mu {\varvec{\Sigma}}} \right\}^{ - 1} {\mathbf{L}}_{{\varvec{\uppsi}}} } \right]^{ - 1} {\mathbf{L}}_{{\varvec{\uppsi}}}^{T} \left\{ {{\mathbf{C}} + \mu {\varvec{\Sigma}}} \right\}^{ - 1} $$](/wp-content/uploads/2016/04/A272390_1_En_16_Chapter_Equ3.gif)
where C represents the data covariance matrix calculated over a time-frequency window of interest,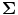 is a diagonal matrix representing the white noise at each of the MEG channels, and μ is a regularisation parameter. In this way, the weights W ψ are derived specifically to reject interference, including that which is correlated across multiple MEG sensors and which might otherwise generate spurious functional connectivity.
is a diagonal matrix representing the white noise at each of the MEG channels, and μ is a regularisation parameter. In this way, the weights W ψ are derived specifically to reject interference, including that which is correlated across multiple MEG sensors and which might otherwise generate spurious functional connectivity.
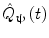 is minimised with a linear constraint that power originating from location/orientation
is minimised with a linear constraint that power originating from location/orientation 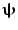 remains. Mathematically:
remains. Mathematically:![$$ \min_{{{\mathbf{W}}_{{\varvec{\uppsi}}} }} \left[ {\varepsilon \left( {\hat{Q}_{{\varvec{\uppsi}}}^{2} } \right)} \right]\quad subject\;to\quad {\mathbf{W}}_{{\varvec{\uppsi}}}^{T} {\mathbf{L}}_{{\varvec{\uppsi}}} = 1 $$](/wp-content/uploads/2016/04/A272390_1_En_16_Chapter_Equ2.gif)
(2)
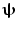 ). Note that the minimisation term ensures that any signal variance not originating from
). Note that the minimisation term ensures that any signal variance not originating from 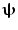 is minimised. An analytical solution to this problem is:
is minimised. An analytical solution to this problem is:![$$ {\mathbf{W}}_{{\varvec{\uppsi}}}^{T} = \left[ {{\mathbf{L}}_{{\varvec{\uppsi}}}^{T} \left\{ {{\mathbf{C}} + \mu {\varvec{\Sigma}}} \right\}^{ - 1} {\mathbf{L}}_{{\varvec{\uppsi}}} } \right]^{ - 1} {\mathbf{L}}_{{\varvec{\uppsi}}}^{T} \left\{ {{\mathbf{C}} + \mu {\varvec{\Sigma}}} \right\}^{ - 1} $$](/wp-content/uploads/2016/04/A272390_1_En_16_Chapter_Equ3.gif)
(3)
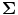 is a diagonal matrix representing the white noise at each of the MEG channels, and μ is a regularisation parameter. In this way, the weights W ψ are derived specifically to reject interference, including that which is correlated across multiple MEG sensors and which might otherwise generate spurious functional connectivity.
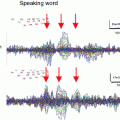
is a diagonal matrix representing the white noise at each of the MEG channels, and μ is a regularisation parameter. In this way, the weights W ψ are derived specifically to reject interference, including that which is correlated across multiple MEG sensors and which might otherwise generate spurious functional connectivity.Rejection of interference by beamforming is highlighted in Fig. 4 (Brookes et al. 2011a). As shown above in Fig. 2, MEG is highly susceptible to interference generated by the magnetocardiogram. In Fig. 4a, b the blue line shows Pearson correlation between the ECG and the MEG sensors most affected by sources in left (A) and right (B) sensorimotor cortices. In contrast, the green line shows correlation between the ECG and the beamformer reconstructed timecourses from the peak voxel of interest in the left (A) and right (B) sensorimotor cortices. Notice that for sensor space data, high correlation with the ECG is observed, and further that correlation is inhomogeneous with respect to frequency, peaking in the low beta band. However, following application of the beamformer, correlation is significantly reduced across all bands. (Note this example uses the same data as that in Fig. 2.) It is clear that, had sensor space functional connectivity been assessed in these data, it is likely that correlations between left and right hemisphere would have been spuriously increased by the common mode cardiac artifact, particularly in the beta band. However this confound has been reduced by beamforming.
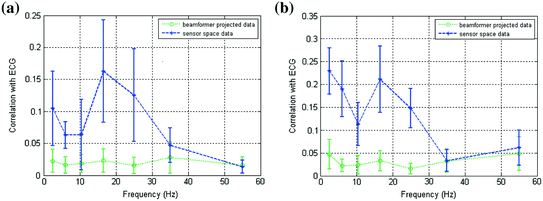

Fig. 4
a Correlation between MEG and ECG plotted as a function of frequency; the blue line shows correlation with sensors most affected by a source in left primary motor cortex; the green line shows correlation with a beamformer reconstructed timecourse for the same source in left motor cortex. b Equivalent to (a) but shown for the right motor cortex. Notice the significant drop in ECG correlation with application of the spatial filter adapted from Brookes et al. (2011a)
2.3 Source Leakage and Desirable Properties of Inverse Solutions
Despite the advantages of source space projection in measurement of functional connectivity, there remain significant problems which, if not controlled, can lead directly to spurious connectivity measurement. The ill-posed nature of the inverse problem causes a degree of spatial blurring (i.e. a single point dipolar source will be spread across a finite volume). In addition, sources can be mislocalised, for example due to inaccuracies in the MEG forward solution (e.g. representing an extended source as a point dipole) or due to incorrect assumptions made by the inverse localisation algorithm used (e.g. suppression of temporally correlated sources using beamforming). These effects combined mean that MEG assessment of electrical activity made at spatially separate brain sites are not necessarily independent. This means that signals originating from a single brain location can “leak” into the estimated signals from other spatial locations. This manifests as apparent ‘signal leakage’ between voxels which can lead to spurious functional connectivity measurement. For this reason, it can be instructive to measure the likely effects of signal leakage prior to functional connectivity assessment.
Signal leakage differs depending on the inverse solution employed and brain area studied; for example leakage tends to be worse for deeper sources where the generated field patterns are more spatially diffuse. Furthermore when using adaptive techniques the leakage profile for any given voxel will change depending on the signal to noise ratio of the MEG data. This makes leakage assessment non-trivial. There are many ways to estimate the extent of source leakage and each has its own advantages and disadvantages. In cases where connectivity assessment involves a priori selection of a seed location, a simple but instructive technique is to measure correlation between the source reconstruction weighting parameters, W ψ, derived for the seed location, and the equivalent weighting parameters for all other voxels in the brain. In an ideal world, the weights for any one voxel would be a unique combination of MEG sensors, however the underdetermined nature of the inverse problem prevents this and there will necessarily be some correlation between weights for voxels in close proximity. Equation 1 shows that if the weights for two spatially separate voxels are correlated (as is likely to be the case for nearby voxels) then the projected signals will also be correlated and this may appear as spurious functional connectivity in source space. If, however, the weights for two voxels are completely independent, but the timecourses from those voxels are highly correlated, it is more likely that genuine FC exists between those two brain locations.
An example of leakage assessment via weights correlation is given in Fig. 5 (Brookes et al. 2011a). Here we compare the case for a spatial matched filter in which the weighting parameters are simply a scaled version of the lead fields, and two instances of weighting parameters derived using regularised beamforming (Eq. 3; μ = 4). Figure 5a shows a volumetric image of Pearson correlation between lead fields at the seed location (placed at the cross hairs) and lead fields at all other source space voxels. This is shown for a single subject (with the source orientation for each voxel derived as the orientation of maximum signal to noise ratio). Pearson correlation coefficients are thresholded at 0.5 for visualisation. Figure 5b, c show volumetric images of correlation between beamformer weights at the seed location and at all other voxels in the brain. (Weights correlation images are computed using 13–20 Hz filtered data.) Figure 5b shows weights correlation in a case where the covariance matrix (C) is based on all available MEG data (25 min for this example experiment); Fig. 5c shows weights correlation in a case where covariance is based on the first 5 min of data only. Notice here that weights correlation is far less widespread than lead field correlation, an effect of the adaptive nature of beamforming which shows that, even if lead fields are correlated, beamformer weights can remain independent. Figure 5d, e show lead field correlation and weights correlation as a function of Euclidean distance from the seed location, respectively. Note the improved spatial resolution of beamformer weights correlation with respect to lead field correlation, that is also apparent in Fig. 5a, b. (Separate lead field correlations for different frequency bands appear because the source orientation is computed independently for each frequency band. Lead fields themselves do not change with frequency.)
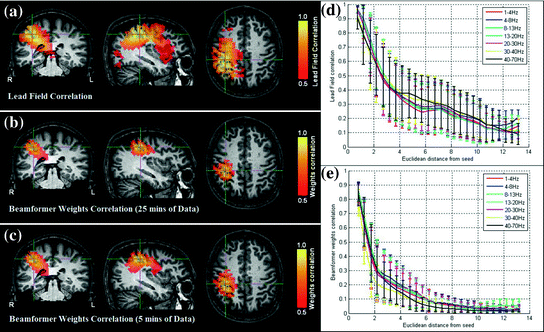

Fig. 5
Signal leakage in beamformer spatial filtering: a Correlation between lead fields at the seed location (cross hairs) and all other brain voxels. b–c Volumetric images of correlation between beamformer weights at a seed location (cross hairs) and all other test voxels in the brain. b Weights computed using 25 min of data (μ = 4; 13–20 Hz band; single subject); c Weights computed using 5 min of data only (μ = 4; 13–20 Hz band; single subject); d Lead field correlation plotted as a function of Euclidean distance from the seed location. e Beamformer weights correlation (Weights computed using 25 min data; μ = 4) plotted as a function of distance from the seed location adapted from Brookes et al. (2011a)
This simple example highlights some of the desirable properties of inverse problem solutions for functional connectivity measurement. Firstly, the spatial extent of weights correlation should be as small as possible. In this example we show that the adaptive nature of beamforming limits the spatial extent of weights correlation compared to a spatial matched filter. Note also that for beamforming, data duration has an effect. In this example the total volume of cortex with weights correlated at 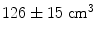 when using 25 min of data; this was compared to
when using 25 min of data; this was compared to 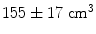 when weights were computed using only the first 5 min (Brookes et al. 2011a). This highlights the importance of judicious experimental design (Brookes et al. 2008), meaning that researchers aiming to assess MEG connectivity based only on 5 min data segments are necessarily going to be more affected by source leakage than those basing measurements on much longer experiments (assuming stationary sources). This is the case for beamforming, however it is not the case for non-adaptive techniques such as certain forms of minimum norm estimation in which weights are based only on system geometry and not the MEG data. Finally, note the inhomogeneous nature of weights correlation. This is particularly notable in Fig. 5a where weights correlation extends asymmetrically from the seed location. For example, here one might spuriously estimate connectivity between the seed in right motor cortex (the cross hairs) and the right insula cortex; however this would be based only on leakage.
when weights were computed using only the first 5 min (Brookes et al. 2011a). This highlights the importance of judicious experimental design (Brookes et al. 2008), meaning that researchers aiming to assess MEG connectivity based only on 5 min data segments are necessarily going to be more affected by source leakage than those basing measurements on much longer experiments (assuming stationary sources). This is the case for beamforming, however it is not the case for non-adaptive techniques such as certain forms of minimum norm estimation in which weights are based only on system geometry and not the MEG data. Finally, note the inhomogeneous nature of weights correlation. This is particularly notable in Fig. 5a where weights correlation extends asymmetrically from the seed location. For example, here one might spuriously estimate connectivity between the seed in right motor cortex (the cross hairs) and the right insula cortex; however this would be based only on leakage.
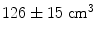 when using 25 min of data; this was compared to
when using 25 min of data; this was compared to 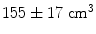 when weights were computed using only the first 5 min (Brookes et al. 2011a). This highlights the importance of judicious experimental design (Brookes et al. 2008), meaning that researchers aiming to assess MEG connectivity based only on 5 min data segments are necessarily going to be more affected by source leakage than those basing measurements on much longer experiments (assuming stationary sources). This is the case for beamforming, however it is not the case for non-adaptive techniques such as certain forms of minimum norm estimation in which weights are based only on system geometry and not the MEG data. Finally, note the inhomogeneous nature of weights correlation. This is particularly notable in Fig. 5a where weights correlation extends asymmetrically from the seed location. For example, here one might spuriously estimate connectivity between the seed in right motor cortex (the cross hairs) and the right insula cortex; however this would be based only on leakage.
when weights were computed using only the first 5 min (Brookes et al. 2011a). This highlights the importance of judicious experimental design (Brookes et al. 2008), meaning that researchers aiming to assess MEG connectivity based only on 5 min data segments are necessarily going to be more affected by source leakage than those basing measurements on much longer experiments (assuming stationary sources). This is the case for beamforming, however it is not the case for non-adaptive techniques such as certain forms of minimum norm estimation in which weights are based only on system geometry and not the MEG data. Finally, note the inhomogeneous nature of weights correlation. This is particularly notable in Fig. 5a where weights correlation extends asymmetrically from the seed location. For example, here one might spuriously estimate connectivity between the seed in right motor cortex (the cross hairs) and the right insula cortex; however this would be based only on leakage.In summary, there are significant advantages in measurement of connectivity in source space over sensor space (Schoffelen and Gross 2009) including increased interpretability with respect to anatomy (Fig. 3) and also improved rejection of non-neuronal artifacts (Fig. 4). However, even if connectivity is measured in source space, it is important to note that electrical activity estimated at spatially separate source space locations are not necessarily independent due to signal leakage and care must be taken to ensure that this effect does not impact on measurements. The leakage problem will be further discussed in Sect. 3.3.5.
3 Measuring Functional Connectivity in MEG
Following projection of MEG data from sensor space to source space, which may be achieved using any inverse projection algorithm whose underlying assumptions are reasonable given the experimental design, one aims to assess connectivity between projected signals. To achieve this there are a variety of linear and non-linear methods available. In this section we describe a number of these techniques.
3.1 The Definition of Functional Connectivity
Functional connectivity is based on quantifying statistical dependencies directly from the data (Friston 2011). These statistical measures typically characterize the similarity between a pair of signals (or more) in terms of quantities such as their amplitude or phase in particular frequency bands. This is in contrast to effective connectivity measures, which are based on generative models of the data, such as Dynamic Causal Modelling (DCM). In fMRI, the term “functional connectivity” has become synonymous with temporal correlation between BOLD signals from spatially separate voxels. However, a number of measures of functional connectivity have also been applied to M/EEG data, with varying levels of success. These include power correlations, mutual information, coherence and phase locking. Unless explicitly stated otherwise, we will assume throughout this chapter that these measures are applied on the timecourses in brain (source) space.
At the outset we should be aware that there are potential problems with the use, and in particular in the interpretation, of functional connectivity. One particularly important issue is well exemplified by the increasingly popular approach of using functional connectivity (in fMRI and M/EEG) as a feature to predict or classify the group from which a particular subject was sampled (Craddock et al. 2009). The problem is that changes in functional connectivity, e.g. between conditions or between two population groups, can occur simply due to changes in the signal-to-noise ratio, or due to changes in other parts of a wider network (sometimes known as the “missing node” problem); even when there is no change in the actual neuronal connectivity. This issue has been well documented elsewhere (Friston 2011).
False positive connectivity can also be inferred if correlations caused by the measurement process itself are not accounted for. In particular, as described in Sect. 2.3, artefactual zero-lag correlations are readily caused due to source leakage (Schoffelen and Gross 2009). These phenomena will tend to contaminate all functional connectivity measures unless accounted for.1 Different ways for accounting for this particular problem will be presented at various points throughout this section, and in particular in Sect. 3.3.5.
Functional connectivity also provides limited insight into the mechanisms of the dynamics that underlie brain activity, and does not directly provide biologically relevant information. In theory, the best way to overcome these limitations is to turn to effective connectivity. However effective connectivity approaches arguably still need substantial development and validation before they can be used in earnest on MEG data. Effective connectivity will be discussed further in the “Future Directions” section in this chapter. Until effective connectivity is indeed rendered “effective”, functional connectivity will remain the dominant approach in use, with the caveat that considerable care must be taken when interpreting the results.
3.2 Linear Metrics
In this section we will consider linear metrics of statistical dependency, or functional connectivity, between brain areas. Clearly the most straightforward of these would be correlation on the raw time series in brain space. However, this is impotent in MEG due to the fact that we do not expect there to be zero lag correlations between distal brain areas. Instead we need turn to more sophisticated measures such as coherence and phase locking.
3.2.1 Coherence and Dynamic Imaging of Coherent Sources
Coherence is a widely used measure of functional connectivity that provides information about the degree of coupling between two signals at a particular frequency. In essence it quantifies linear correlations in the frequency domain. The coherence 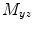 between a dipole timecourse
between a dipole timecourse 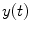 and a reference signal
and a reference signal 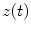 is defined as the magnitude squared cross spectral density of the two signals divided by the autospectral density of each signal:
is defined as the magnitude squared cross spectral density of the two signals divided by the autospectral density of each signal:
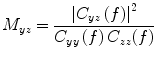
where 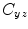 is the cross-spectral density between signals y and z, and
is the cross-spectral density between signals y and z, and 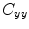 and
and 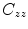 are the autospectral densities of signals y and z respectively. The calculation of coherence is a function of frequency, f, and depends on the frequency band over which the cross-spectral density is computed. The cross-spectral density between the two signals may be calculated in the frequency domain as the complex conjugate product of the Fourier transformed data
are the autospectral densities of signals y and z respectively. The calculation of coherence is a function of frequency, f, and depends on the frequency band over which the cross-spectral density is computed. The cross-spectral density between the two signals may be calculated in the frequency domain as the complex conjugate product of the Fourier transformed data 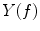 and
and 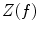 :
:
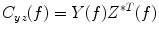
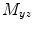 between a dipole timecourse
between a dipole timecourse  and a reference signal
and a reference signal  is defined as the magnitude squared cross spectral density of the two signals divided by the autospectral density of each signal:
is defined as the magnitude squared cross spectral density of the two signals divided by the autospectral density of each signal: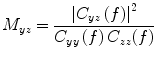
(4)
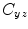 is the cross-spectral density between signals y and z, and
is the cross-spectral density between signals y and z, and 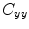 and
and 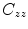 are the autospectral densities of signals y and z respectively. The calculation of coherence is a function of frequency, f, and depends on the frequency band over which the cross-spectral density is computed. The cross-spectral density between the two signals may be calculated in the frequency domain as the complex conjugate product of the Fourier transformed data
are the autospectral densities of signals y and z respectively. The calculation of coherence is a function of frequency, f, and depends on the frequency band over which the cross-spectral density is computed. The cross-spectral density between the two signals may be calculated in the frequency domain as the complex conjugate product of the Fourier transformed data 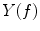 and
and 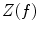 :
: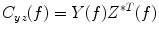
(5)
Coherence values lie in the range 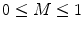 , with a value of 1 indicating that the signals are perfectly coupled in frequency. At a given frequency, if the phase of one signal is fixed relative to the other then the signals can have a high coherence at that frequency.
, with a value of 1 indicating that the signals are perfectly coupled in frequency. At a given frequency, if the phase of one signal is fixed relative to the other then the signals can have a high coherence at that frequency.
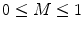 , with a value of 1 indicating that the signals are perfectly coupled in frequency. At a given frequency, if the phase of one signal is fixed relative to the other then the signals can have a high coherence at that frequency.
, with a value of 1 indicating that the signals are perfectly coupled in frequency. At a given frequency, if the phase of one signal is fixed relative to the other then the signals can have a high coherence at that frequency.Coherence has been widely used for measuring connectivity in MEG, largely thanks to the popular dynamic imaging of coherent sources (DICS) method (Gross et al. 2001), which uses a frequency domain beamformer to localise sources coherent with a reference signal. The reference signal may be from a cortical location, or an externally measured device (e.g. electrode). This has been shown to work particularly well between cortical sources in MEG and EMG hand movement measurements in motor experiments (Gross et al. 2001), but also between brain regions during a task (Kujala et al. 2007). It should be noted that while DICS computes the cross-spectral density matrix in sensor space, and then applies an adaptive spatial filter (beamformer) to reconstruct source power and coherence for a given frequency bin or band; it can be shown that this is equivalent to using a time-domain beamformer (Woolrich et al. 2011) followed by computation of coherence in source space.
As discussed above, vanilla coherence will be susceptible to false positives due to artefactual zero-lag correlations due to the source leakage problem. A modification to coherence that can overcome this problem is to use imaginary coherence (Nolte et al. 2004), which works by only using the imaginary terms. These terms cannot be influenced by zero lagged correlations, and so necessarily represent true interactions between brain areas occurring with a certain time (phase) lag:
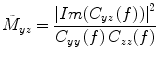
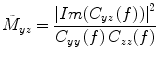
(6)
Measures like imaginary coherence have been used to investigate functional connectivity in patients with brain lesions using resting state MEG (Guggisberg et al. 2008). However, in some resting state MEG studies it is has been shown to be less effective for estimating cortico-cortical interactions than power correlation methods, such as when looking for inter hemispheric connectivity between the left and right motor cortex (Brookes et al. 2011a).
3.2.2 Phase Locking
It has been argued that one of the problems with coherence is that it is not a pure measure of the phase relationship. In other words, it also increases with amplitude covariance, and the relative importance of amplitude and phase covariance in the coherence value is not clear (Lachaux et al. 1999). An alternative is to use a measure that specifically identifies when there is frequency specific transient phase locking. The phase-locking value (PLV) is one example of such a measure.
To estimate PLV, we start by extracting the timecourse of the instantaneous phase of two signals x and y (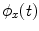 and
and 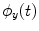 , respectively) at the frequency of interest, f. Typically, this is done by band-pass filtering the data, and then computing a time-frequency transform (e.g. Wavelet or Stockwell). We can then compute the phase difference at each time point,
, respectively) at the frequency of interest, f. Typically, this is done by band-pass filtering the data, and then computing a time-frequency transform (e.g. Wavelet or Stockwell). We can then compute the phase difference at each time point, 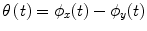 . The phase locking value (PLV) is then given by:
. The phase locking value (PLV) is then given by:
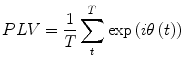
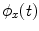 and
and 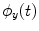 , respectively) at the frequency of interest, f. Typically, this is done by band-pass filtering the data, and then computing a time-frequency transform (e.g. Wavelet or Stockwell). We can then compute the phase difference at each time point,
, respectively) at the frequency of interest, f. Typically, this is done by band-pass filtering the data, and then computing a time-frequency transform (e.g. Wavelet or Stockwell). We can then compute the phase difference at each time point, 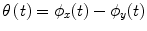 . The phase locking value (PLV) is then given by:
. The phase locking value (PLV) is then given by: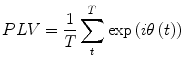
(7)
We can look also for phase locking with regards to finding consistent phase difference over repeats of a stimulus in multi-trial (epoched) data at the same time point, t, within trial. In this case we have (Lachaux et al. 1999):
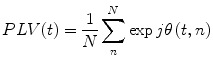
where n indexes the N repeated trials. Note that this is related to the Inter-trial Coherence (ITC), which is a univariate measure looking for consistent phase locking over trials in a single brain area at a time. When interpreting multi-trial PLV, it is important to be aware that if the two brain areas in question are both separately responding in a stimulus-locked manner (as in an event related field) to the underlying stimulus, then a significant PLV could result even though the two areas are not necessarily directly interacting. Note that this issue of interpretation in the face of what corresponds to the “missing nodes” problem is not specific to PLV, but is a problem inherent to all functional connectivity measures.
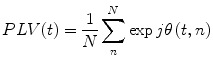
(8)
One important consideration in the measurement of phase locking is how to choose an appropriate bandwidth. This is a trade-off; the bandwidth needs to be sufficiently specific for the concept of phase to be meaningful, but not too narrow as to make estimation excessively noisy. Like coherence, PLV is a symmetric measure and so does not allow direct inference about directionality between areas. Nonetheless, phase locking measures have been successfully used in task MEG data, notably to detect distributed visuo-motor networks, including structures of the frontoparietal circuit and the cerebello-thalamo-cortical pathway (Jerbi et al. 2007).
Phase lag index (PLI) can be thought of as being the same to PLV as imaginary coherence is to coherence (Stam et al. 2007). In other words PLI is a modification of the PLV measure such that it is protected from contamination due to artifactual zero-lag correlations caused by source leakage. PLI works by defining an asymmetry index for the distribution of phase differences. If no phase coupling exists between two time series, then this distribution is expected to be flat. Any deviation from this flat distribution indicates phase synchronization. Pure zero lag phase locking due to field spread will manifest as a symmetric distribution around zero phase lag, and so will not adversely influence PLI.
3.3 Nonlinear Metrics
3.3.1 Band Limited Power Correlations
Perhaps the simplest non-linear methodology for measurement of functional connectivity is to assess correlations between either the amplitude or power envelope of band limited oscillations. These envelopes have been shown to exhibit temporal variation over time scales of seconds and in some cases even minutes. Invasive measurements have shown that correlations between band limited power envelopes fall off with distance, yet much more gradually than the correlations in the raw high-frequency local field potentials from which envelopes are derived (Leopold et al. 2003). Spontaneous gamma band limited power fluctuations recorded from depth electrodes in epileptic patients (Nir et al. 2008) revealed correlations between bilateral homotopic brain regions, which is consistent with numerous fMRI functional connectivity studies. Furthermore a large amount of work has shown a relationship between the BOLD response and changes in MEG oscillatory power during a task (Brookes et al. 2005; Singh et al. 2002; Winterer et al. 2007; Zumer et al. 2009) and this implies that if the haemodynamic networks observed using fMRI are visible to MEG, then assessment of band limited power correlation should be informative.
There are numerous techniques by which to compute either band limited amplitude envelope, or band limited power envelope; here we describe a popular approach based on a Hilbert Transform. In source space, having computed the timecourse of electrical activity in some band of interest, 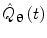 , for each voxel, the analytic signal
, for each voxel, the analytic signal 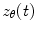 is given by:
is given by:
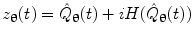
where 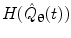 represents the Hilbert transform of
represents the Hilbert transform of 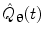 and is given by:
and is given by:
![$$ H[\hat{Q}_{{\varvec{\uptheta}}} (t)] = P\left[ {\frac{1}{\pi }\int_{ - \infty }^{\infty } {\frac{{\hat{Q}_{{\varvec{\uptheta}}} (u)}}{t - u}du} } \right] $$](/wp-content/uploads/2016/04/A272390_1_En_16_Chapter_Equ10.gif)
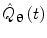 , for each voxel, the analytic signal
, for each voxel, the analytic signal 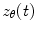 is given by:
is given by: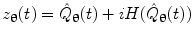
(9)
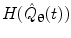 represents the Hilbert transform of
represents the Hilbert transform of 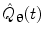 and is given by:
and is given by:![$$ H[\hat{Q}_{{\varvec{\uptheta}}} (t)] = P\left[ {\frac{1}{\pi }\int_{ - \infty }^{\infty } {\frac{{\hat{Q}_{{\varvec{\uptheta}}} (u)}}{t - u}du} } \right] $$](/wp-content/uploads/2016/04/A272390_1_En_16_Chapter_Equ10.gif)
(10)
P denotes the Cauchy principal value of the integral and is used to take account of the singularity at 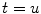 . The magnitude of the analytic signal yields the envelope of the measured oscillatory activity thus:
. The magnitude of the analytic signal yields the envelope of the measured oscillatory activity thus:
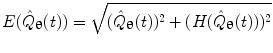
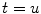 . The magnitude of the analytic signal yields the envelope of the measured oscillatory activity thus:
. The magnitude of the analytic signal yields the envelope of the measured oscillatory activity thus: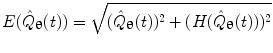
(11)
Hilbert envelopes, 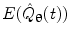 can be computed for every voxel in the source space.
can be computed for every voxel in the source space.
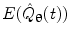 can be computed for every voxel in the source space.
can be computed for every voxel in the source space.Following computation of the band limited amplitude envelopes at all locations in the brain, a metric of connectivity between two voxels can be formulated via computation of a Pearson correlation coefficient between Hilbert envelopes at a seed voxel of interest, and some other test voxel (Brookes et al. 2011a). Mathematically, the Pearson product moment correlation coefficient is given by:
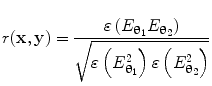
where θ 1 and θ 2




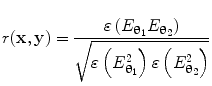
(12)
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree