Introductory Math
Introduction
In this chapter, we review some of the basic mathematical concepts that are used in MR imaging. We don’t want to scare you away so we keep things as simple as possible. An understanding of these basic concepts will help the reader a great deal to comprehend the subtleties of MR imaging and obtain the necessary tools for manipulating the scan parameters to improve the quality of the images.
It is not that important to memorize these mathematical formulas; what’s crucial is the understanding of the concepts behind these formulas. In this chapter, we hope to emphasize the most important mathematical concepts of MRI physics.
Sinusoidals
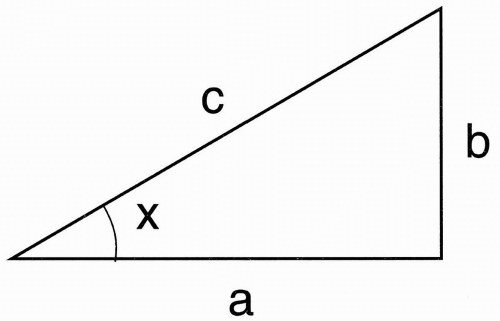
Consider a right triangle (having a right angle) with sides a and b and hypotenuse c and angle x formed by a and c (Fig. 1-1). We can define sin x (read sine of x), cos x (read cosine of x), tan x (read tangent of x), cotan x (read co-tangent of x), and arctan x (read arc-tangent of x) in terms of a, b, and c:
Table 1-1 | |||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
sin x = b/c
cos x = a/c
tan x = sin x/cos x = a/b
arctan b/a = arctan(tan x) = x (Eqn. 1-1)
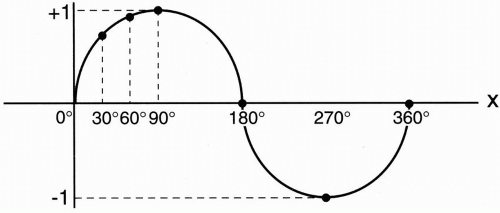
The variable x can be represented in degrees, that is, 45°, 90°, and 180°, or it can be represented in radians, that is, π/4, π/2, and π, where π = 180°. Table 1-1 shows x versus. sin x, cos x, and tan x, where 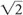 ≅ 1.4 so
≅ 1.4 so 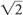 /2 ≅ 0.7 and
/2 ≅ 0.7 and 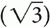 ≅ 1.7 so
≅ 1.7 so 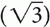 /2 ≅ 0.85.
/2 ≅ 0.85.
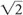 ≅ 1.4 so
≅ 1.4 so 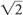 /2 ≅ 0.7 and
/2 ≅ 0.7 and 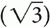 ≅ 1.7 so
≅ 1.7 so 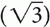 /2 ≅ 0.85.
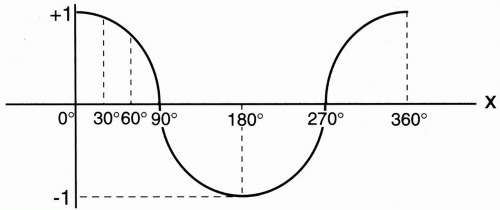
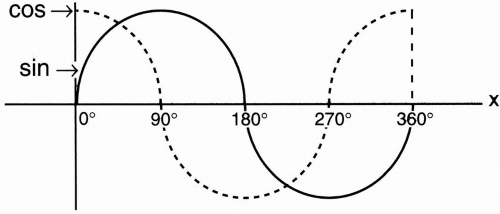
/2 ≅ 0.85.Let’s plot x versus sin x (Fig. 1-2). This is called a sinusoidal function. What about cos x? (Fig. 1-3). Let’s now draw cos x and sin x on a single graph (Fig. 1-4). We can appreciate the symmetry between sin x and cos x. The difference between the two functions is that sin x is shifted to the right of cos x by 90°. Later, when we talk about phase and phase shifts, this mathematical concept will become more important. We can think of sin x as being cos x with a phase difference of 90°.
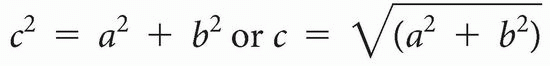
By Equation 1-1
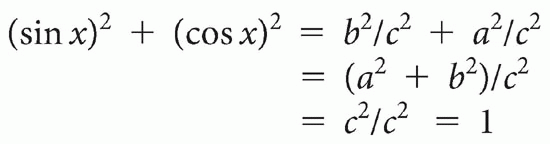
So (sin x)2 + (cos x)2 = 1 If we go back to our graph of sin x and cos x (Fig. 1-4), we can see graphically that because of the phase difference between the cos x and sin x, the sum of their squares will always equal 1. Another way of looking at sine and cosine is to consider a circle with a radius of 1 (Fig. 1-5). To understand this concept, it is necessary to bring up the concepts of vectors, imaginary numbers, and exponentials.
Vector. We’ll designate a vector by using a letter such as v with an arrow above it ( ). This concept will become important later on in the understanding of resonance of spins and dephasing. A vector is a mathematical entity that has both a magnitude and a direction. For example, speed is not a vector—it only has magnitude.
). This concept will become important later on in the understanding of resonance of spins and dephasing. A vector is a mathematical entity that has both a magnitude and a direction. For example, speed is not a vector—it only has magnitude.
Velocity, however, is a vector—it has both magnitude and direction. Another example of a vector is force that describes a magnitude (weight) and a direction (direction where the force is applied).
 ). This concept will become important later on in the understanding of resonance of spins and dephasing. A vector is a mathematical entity that has both a magnitude and a direction. For example, speed is not a vector—it only has magnitude.
). This concept will become important later on in the understanding of resonance of spins and dephasing. A vector is a mathematical entity that has both a magnitude and a direction. For example, speed is not a vector—it only has magnitude. Velocity, however, is a vector—it has both magnitude and direction. Another example of a vector is force that describes a magnitude (weight) and a direction (direction where the force is applied).
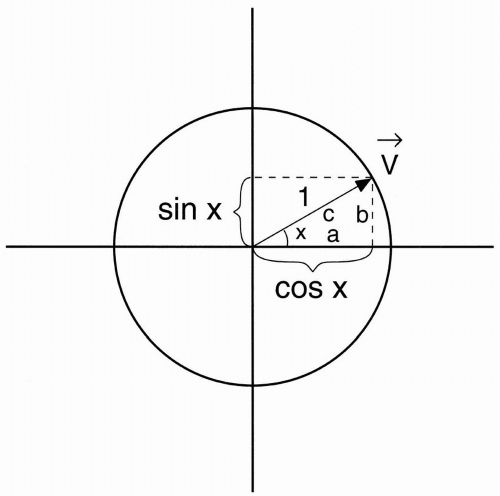 Figure 1-5. A vector v with magnitude 1 and angle x to the horizontal. cos x and sin x are the horizontal and vertical components of this vector, respectively. |
The vector that we’ve drawn in the circle (Fig. 1-5) has a magnitude of 1. The angle between the vector and the horizontal axis is denoted x. If we draw perpendiculars from the vector both horizontally and vertically, we’ll get two components of the vector:
The horizontal component of the vector would correspond to cos x. (Remember that the ratio a/c in Figure 1-1 is cos x.)
The vertical component of the vector would correspond to sin x. (Remember that the ratio b/c in Figure 1-1 is sin x.)
Imaginary Numbers. A positive number n2 has two square roots, + n and − n. For example,
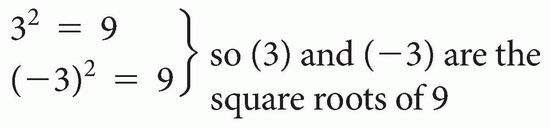
It is impossible to square a real number and have a negative product. Therefore, we shall make up an entity and call the number  an imaginary number. Any of the following would be imaginary numbers:
an imaginary number. Any of the following would be imaginary numbers:
 an imaginary number. Any of the following would be imaginary numbers:
an imaginary number. Any of the following would be imaginary numbers: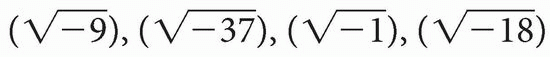
Imaginary numbers can be manipulated in the following way:
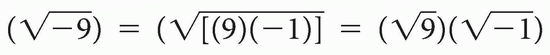
Any imaginary number can be written as a positive number times (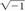 ). The expression (
). The expression (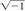 ) is designated by the letter “i”. (Mathematicians use the symbol i to denote an imaginary number, whereas engineers use the symbol “j” in lieu of i because i is reserved to symbolize electric current!) The symbol i is then known as the imaginary unit. In other words, i × i = −1.
) is designated by the letter “i”. (Mathematicians use the symbol i to denote an imaginary number, whereas engineers use the symbol “j” in lieu of i because i is reserved to symbolize electric current!) The symbol i is then known as the imaginary unit. In other words, i × i = −1.
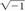 ). The expression (
). The expression (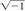 ) is designated by the letter “i”. (Mathematicians use the symbol i to denote an imaginary number, whereas engineers use the symbol “j” in lieu of i because i is reserved to symbolize electric current!) The symbol i is then known as the imaginary unit. In other words, i × i = −1.
) is designated by the letter “i”. (Mathematicians use the symbol i to denote an imaginary number, whereas engineers use the symbol “j” in lieu of i because i is reserved to symbolize electric current!) The symbol i is then known as the imaginary unit. In other words, i × i = −1.Example
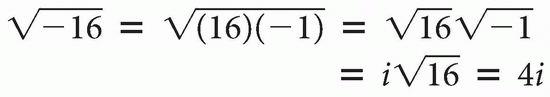
So i is an imaginary number. It doesn’t exist. When you take a square root of a number, it has to be a positive number. However, in this case, if we multiply i by i, we get (−1). Therefore, i is an imaginary number that doesn’t exist.
Complex Numbers. A complex number is a number that has both a real and an imaginary component: Complex = real + imaginary
Example
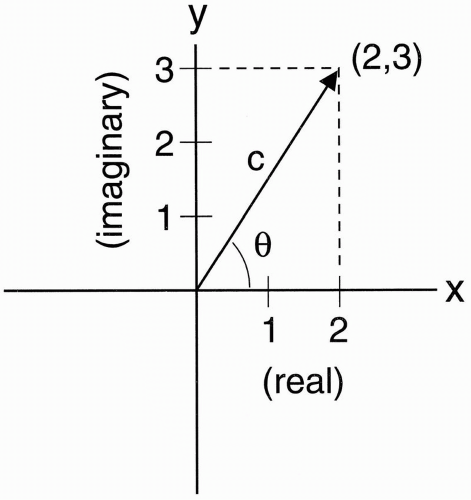
Let’s say a complex number has two components: 2 and 3. The imaginary component is multiplied by (i), where i = 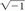 is the imaginary unit. Then, c = (2) + i(3) If you draw this complex number on an x − y plane (Fig. 1-6), the vector (2,3) illustrates the complex number 2 + 3i. Usually you only care about the real part of a complex number, but it makes life easier to deal with the complex number and carry all the computations using complex numbers or vectors and then, at the end, just keep the real part.
is the imaginary unit. Then, c = (2) + i(3) If you draw this complex number on an x − y plane (Fig. 1-6), the vector (2,3) illustrates the complex number 2 + 3i. Usually you only care about the real part of a complex number, but it makes life easier to deal with the complex number and carry all the computations using complex numbers or vectors and then, at the end, just keep the real part.
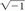 is the imaginary unit. Then, c = (2) + i(3) If you draw this complex number on an x − y plane (Fig. 1-6), the vector (2,3) illustrates the complex number 2 + 3i. Usually you only care about the real part of a complex number, but it makes life easier to deal with the complex number and carry all the computations using complex numbers or vectors and then, at the end, just keep the real part.
is the imaginary unit. Then, c = (2) + i(3) If you draw this complex number on an x − y plane (Fig. 1-6), the vector (2,3) illustrates the complex number 2 + 3i. Usually you only care about the real part of a complex number, but it makes life easier to deal with the complex number and carry all the computations using complex numbers or vectors and then, at the end, just keep the real part.Magnitude and Angle. Sometimes, however, the imaginary part is also helpful. For example, consider Figure 1-6. In this diagram, if we take
the tangent of the angle between the vector and the x-axis, we get tan θ = 3/2 = imaginary/real In other words, the ratio of the imaginary part to the real part gives us the tangent of the angle. The magnitude of the vector (sometimes called the modulus) is given by the Pythagorean theorem
the tangent of the angle between the vector and the x-axis, we get tan θ = 3/2 = imaginary/real In other words, the ratio of the imaginary part to the real part gives us the tangent of the angle. The magnitude of the vector (sometimes called the modulus) is given by the Pythagorean theorem
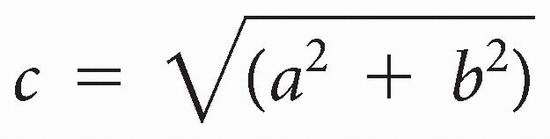
Thus, vector magnitude
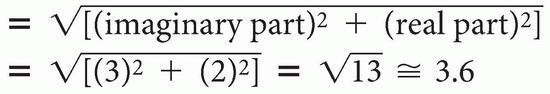
When you’re dealing with a complex number, if you take the ratio of the imaginary part to the real part, you get some sort of measure of the angle of the vector. If you sum the squares of the imaginary and real part, you get the magnitude of the vector (squared).
Function. A mathematical function, designated as f (x), is an entity that varies with respect to a variable, x. For example, sin x is a function that varies with respect to x in a sinusoidal manner, as we saw earlier in the chapter.
Signal. A signal is a time-varying function, that is, something that varies over time, usually millivolts versus time. If the x-axis is time, and the y-axis is magnitude, then a signal is a waveform that varies in magnitude with time.
In an electrical system, a signal is a timevarying current or voltage that can be measured. In MRI, the signal is just a current or voltage that is induced by an oscillating magnetic field. Some signals are periodic—they repeat themselves—as the sine wave or cosine wave repeats itself.
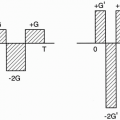
Frequency, Period, and Cycle. Let’s now introduce the concepts of frequency and period. Every periodic function has a frequency, which we will call f. If we measure the time interval between two peaks (or where the signal crosses 0), this interval is called a period, and we’ll denote this by T. Now, frequency = 1/period = 1/T: f = 1/T A cycle in a periodic function is any part of the function over one period. For example, let’s say that we have three complete cycles occurring in 1 sec (Fig. 1-7). In this case, 3 periods take 1 sec 3T = 1 sec T = 1/3 sec Frequency = f = 1/T = 3 cycles per sec = 3 Hz The unit we use to describe frequency is Hertz or Hz (for cycles per sec). There are 2π radians in one cycle. That is to say,
f = frequency when we refer to linear frequency in cycles per sec
ω = frequency when we refer to angular frequency




Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


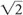 )/2
)/2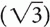 )/2
)/2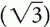 )/2
)/2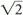 )/2
)/2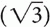 )
)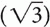 )
)