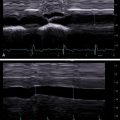
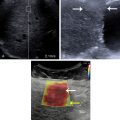
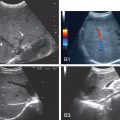
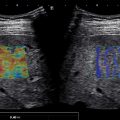
Liver stiffness measurement techniques: Basics

Introduction to stiffness

Liver diseases, such as nonalcoholic fatty liver disease (NAFLD)/nonalcoholic steatohepatitis (NASH), alcoholic liver disease, viral hepatitis as well others, may be characterized by the accumulation of extracellular matrix material (collagen, fibronectin, proteoglycans, and glycosaminoglycans), fats and triglycerides, or tissue scarring, all of which increase tissue stiffness. Biologically, tissue stiffness is important for resisting forces at the cellular, intracellular, and super-cellular levels and for guiding the migration of cells via durotaxis. Though chronic liver diseases can present with increased tissue stiffness, they often also present asymptomatically with normal laboratory tests and imaging results. Since the advent of objective measures of liver stiffness through elasticity imaging, liver stiffness has proven an accurate surrogate biomarker for many liver diseases.

In contrast to traditional B-mode ultrasound imaging, which detects reflections due to differences in the acoustic properties in the underlying tissue, elasticity imaging relies upon differences in mechanical properties of soft tissue. Therefore, understanding elasticity imaging techniques requires understanding mechanical and acoustic properties of soft tissue, mechanisms to perturb tissue, and mechanisms to measure tissue displacement.

Soft tissue mechanics

Material stiffness, or elasticity, is a measure of the degree of resistance to elastic deformation in response to an applied force. Stiffness is measured in terms of pressure in Pascals and is calculated as the ratio between the applied stress (applied force per unit area) and resulting strain (change in length per unit length) of a material. Stress and strain are second-order tensor quantities and together completely describe the state of deformation of a material. Elasticity imaging thereby relies upon disturbing soft tissue with an external force and measuring the tissue’s displacement to calculate stiffness as a biomarker for disease. Deriving tissue stiffness in terms of measurable quantities utilized by common imaging techniques follows.

Stress can be represented as

𝜎ij=∫𝑓𝑖𝑑𝑥𝑗=∫𝜌𝛼𝑖𝑑𝑥𝑗σij=∫fidxj=∫ραidxj
σij=∫fidxj=∫ραidxj

where 𝑎→
a →
is particle acceleration, 𝑓→
f →
represents applied force per unit volume, ρ is material density, and σ _ijis the stress tensor. In elasticity imaging methods, the force is commonly applied using static external compression, acoustic radiation force, or an external vibration mechanism. The material density is commonly assumed to be that of water and is not estimated from the imaging data.

The strain tensor, 𝜀ij
ε ij
, can be represented as

𝜀ij=12(𝑑𝑢𝑖𝑑𝑥𝑗+𝑑𝑢𝑗𝑑𝑥𝑖+𝑑𝑢𝑗𝑑𝑥𝑖𝑑𝑢𝑖𝑑𝑥𝑗)εij=12(duidxj+dujdxi+dujdxiduidxj)
εij=12(duidxj+dujdxi+dujdxiduidxj)

where 𝑢→
u →
represents displacement. Displacement is commonly measured in ultrasonic imaging modalities by correlating time shifts using ultrasonic radio frequency data, phase shifts of in-phase and quadrature (IQ) data ^, at a pulse repetition frequency of several kilohertz.

However, for complex, nonhomogenous, nonlinear materials or for complex applied stress fields (e.g., those generated from focused acoustic radiation force), it can be difficult to derive stress–strain relations that model elasticity under any loading. Soft tissues are viscoelastic (strain dependent on rate of stress application), nonhomogenous, and anisotropic (stress–strain response is orientation dependent). To simplify modeling of soft tissue complexity, many assumptions are made to model linear, elastic behavior under loading used in imaging.

Assuming small strains, soft tissues can be described as linear, elastic solids.

Three moduli are used to characterize the material’s elastic properties: Young’s modulus, E , which describes resistance to deformation uniaxially; shear modulus or rigidity, G or μ , which characterizes resistance to shear; bulk modulus, 𝐾
K
, which measures a material’s resistance to compression. Deformation orthogonal to the axis of loading is described by Poisson’s ratio, 𝑣
v
. Three linear elastic constitutive equations relate these four constants,