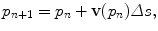Fig. 1
Sketch of HARDI reconstruction techniques
In this chapter, we focus on deterministic and probabilistic tractography using state of the art reconstruction of the diffusion and fibre ODF from QBI. QBI is of interest because it is model-free and it can be computed analytically and robustly with low computational cost [23]. First, we review the existing HARDI reconstruction techniques and state of the art HARDI-based tractography algorithms to put our new methods into context. Then, we develop our analytical solution to reconstruct the diffusion ODF and the fibre ODF from QBI data. Finally, we describe a new deterministic tractography algorithm and a new probabilistic tractography algorithm able to recover complex fibre tracts with known crossing, fanning and branching configurations. Most current DTI based methods neglect these fibres, which might lead to wrong interpretations of the brain functions.
2 Prior Art
HARDI samples q-space along as many directions as possible in order to reconstruct estimates of the true diffusion probability density function (PDF) of water molecules. This true diffusion PDF is model-free and can recover the diffusion of water molecules in any underlying fibre population. HARDI depends on the number of measurements N and the gradient strength (b-value), which will directly affect acquisition time and signal to noise ratio in the signal. Typically, there are currently two strategies used in HARDI: 1) sampling of the whole q-space 3D Cartesian grid or 2) single shell spherical sampling.1 In the first case, a large number of q-space points are taken over the discrete grid (N > 200) and the inverse Fourier transform of the measured DW signal is taken to obtain an estimate of the diffusion PDF. This is q-space imaging (QSI) and DSI [69]. The method requires very strong imaging gradients (500 ≤ b ≤ 20000 s/mm2) and a long time for acquisition (15-60 minutes) depending on the number of sampling directions. In the second case, a uniform sampling of a single sphere is done for a certain radius in q-space (given by the b-value). Typically, 60 ≤ N ≤ 200, b ≥ 1000 s/mm2 is used and acquisition time is between 10 and 20 minutes.
2.1 Review of HARDI Reconstruction Techniques
The goal of HARDI is to capture multiple fibre directions within the same imaging voxel. Some HARDI reconstruction techniques are model dependent, some model-free, some have linear solutions whereas others require non-linear optimization schemes. A schematic view of the major multiple fibre HARDI reconstruction algorithms is shown in Fig. 1. A good review of these methods up to 2005 can be found in [2]. We now summarize the major techniques.
It is a simple extension of the DTI model to assume that a mixture of Gaussians can describe the diffusion PDF. [65] proposed the initial solution and many other works [1, 13, 18, 48, 55, 65, 67] proposed variants of the multi-Gaussian with constraints such as forcing symmetry of eigenvalues, forcing certain magnitude and ratios of eigenvalues or imposing positive definiteness of the DT (see [2]). A similar approach to multi-Gaussian modeling is the ball & stick mixture model. It assumes that water molecules in an imaging voxel belong to one of two populations, a restricted population within or near fibre structures (stick), modeled with an anisotropic Gaussian distribution, and a free population that is not affected by fibre structure barriers (ball), modeling by an isotropic Gaussian distribution. The approach extends to a mixture of restricted compartments and is thus able to recover multiple fibre compartments [10, 33]. Another similar approach is the CHARMED technique [7]. This technique assumes a highly restricted compartment that is non-Gaussian and a hindered compartment that is approximately Gaussian. The approach can also be formulated as a mixture of restricted compartments and is thus able to recover multiple fibre compartments. The multi-Gaussian, ball & stick and CHARMED all suffer from the same shortcomings regarding model selection and numerical implementation. One must select the number of compartments a priori, one must use non-linear optimization to solve for the parameters and the methods are sensitive to noise and to the number of measurements.
Spherical deconvolution (SD) methods generalize the mixture modeling methods of the previous section by assuming a distribution of fibre orientations to overcome the limitation of the number of compartment selection n. The original SD method [64] was improved in [4, 20, 37, 40, 57] using non-linear optimization techniques that better deal with the SD instabilities, noise and negative diffusion appearing in the deconvolution process. A recent review SD methods can be found in [37]. In [38], the case of multiple fibre bundles is handled in a similar way to the SD methods. The novelty is that each fibre bundle is represented by a Wishart distribution. This leads to a reformulation of DTI in the presence of a single orientation but is also able to account for multiple fibre crossings. In contrast, in [49], the diffusion ODF is modeled with a mixture of von Mises-Fisher distributions, which allows for the definition of a closed-form Riemannian distance between diffusion ODFs.
Another model-independent method reconstructs the radially persistent angular structure (PAS) [2, 34] of the diffusion PDF. The reconstruction forces probabilities to be non-zero only on a spherical shell of a certain radius. The PAS reconstruction is non-linear and computationally very heavy but recent efforts [61] have been done to propose a linearized solution to PAS-MRI based on the fact that it is a special case of SD methods (relation indicated by an arrow between SD and PAS-MRI in Fig. 1).
Finally, the diffusion orientation transform (DOT) proposed in [52] is yet another model-independent reconstruction algorithm. The DOT is a function that maps the apparent diffusion coefficient (ADC) profile to the diffusion PDF. Using similar techniques, [51] fit high-order tensors (HOT) to the HARDI measurements to model the ADC. ADC modeling is not discussed in this chapter because it is not an appropriate function for fibre tractography (see [22]) but it can also be modeled with spherical harmonics (SH) [3, 26] or generalized DTI (gDTI) [47]. Finally, similar to QBI, the DOT has a possible multiple shell HARDI extension with the bi and tri exponential fit [52].
2.2 Review of HARDI-Based Tractography Algorithms
In tractography, two families of algorithms exist: deterministic and probabilistic algorithms. Research groups have recently started to generalize both deterministic and probabilistic DT-based tracking algorithms to use HARDI reconstruction methods mentioned in the previous section. Some of these methods use the principal direction extracted from the diffusion ODF computed from DSI [30, 65], from a multi-tensor/Gaussian local model [12, 28, 43, 53], or from a q-ball diffusion ODF [14, 17]. In this chapter, we propose another extension to streamline tractography based on the multiple maxima information of the fibre ODF.
Deterministic tractography algorithms inherit the classical limitations of deterministic algorithms such as choice of initialization [39], sensitivity in estimated principal direction and lack of straightforward way to compute statistics on tracts and lack of connectivity information between regions of the brain [65]. To overcome limitations of deterministic tractography, DT-based probabilistic [11, 27, 42, 44, 53] and geodesic [35, 45] algorithms have been used. Probabilistic algorithms are computationally more expensive than deterministic algorithms but can better deal with partial volume averaging effects and noise uncertainty in underlying fibre direction and output a connectivity index measuring how probable two voxels are connected to one another.
HARDI-based probabilistic tractography have recently been published in the literature [10, 16, 31, 36, 40, 54, 56, 59, 62] to generalize several existing DT-based methods. First, in [40] parametric SD is used and in [10] a mixture of Gaussian model is used to extend the probabilistic Bayesian DT-based tracking [11]. Related to these techniques, [36] uses a Bayesian framework to do global tractography instead of tracking through local orientations. In [56], Monte Carlo particles move inside the continuous field of q-ball diffusion ODF and are subject to a trajectory regularization scheme. In [31, 54], an extension to their DT-based approach [53] is also proposed using a Monte Carlo estimation of the white matter geometry and recently, a Bingham distribution is used to model the peak anisotropy in the fibre distributions [62]. Finally, in [16], large number of M-FACT QBI streamlines are reconstructed and all pathways are reversed-traced from their end points to generate of map of connection probability. In this chapter, our new probabilistic algorithm is based the fibre ODF using a Monte Carlo random walk algorithm.
3 Analytical Solution to Q-Ball Imaging
QBI [66] is a model-independent method to estimate the diffusion ODF. This diffusion ODF contains the full angular information of the diffusion PDF and is defined as
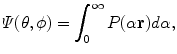
where (θ, ϕ) obey physics convention (θ ∈ [0, π], ϕ ∈ [0, 2π]). [66] showed that it was possible to reconstruct a smoothed version of the diffusion ODF directly from single shell HARDI acquisition with the Funk-Radon transform (FRT). Intuitively, the FRT value at a given spherical point is the great circle integral of the signal on the sphere defined by the plane through the origin perpendicular to the point of evaluation. The original QBI has a numerical solution [66] and more recent methods [5, 23, 32] have introduced an analytical spherical harmonic reconstruction solution that is faster and more robust. To develop the analytical solution to QBI, we first need to estimate the HARDI signal with spherical harmonics (SH) and then, to solve the FRT analytically with SH.
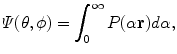
(1)
Letting Y ℓ m denote the SH of order ℓ and degree m (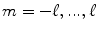 ), we define a modified SH basis that is real and symmetric. For even order ℓ, we define a single index j in terms of ℓ and m such that
), we define a modified SH basis that is real and symmetric. For even order ℓ, we define a single index j in terms of ℓ and m such that 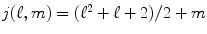 . The modified basis is given by
. The modified basis is given by
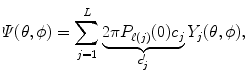
where 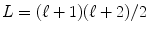 is the number of elements in the spherical harmonic basis, c j are the SH coefficients describing the input HARDI signal, P ℓ(j) is the Legendre polynomial of order ℓ(j)2 and c′ j the coefficients describing the ODF Ψ. Here, we estimate the c j coefficients with the solution presented in [23] with a Laplace-Beltrami regularization of the SH coefficients c j to obtain a more robust ODF estimation. The detailed implementation of the Laplace-Beltrami regularization and the comparison with the state of the art methods [5, 32] are presented in [22, 23].
is the number of elements in the spherical harmonic basis, c j are the SH coefficients describing the input HARDI signal, P ℓ(j) is the Legendre polynomial of order ℓ(j)2 and c′ j the coefficients describing the ODF Ψ. Here, we estimate the c j coefficients with the solution presented in [23] with a Laplace-Beltrami regularization of the SH coefficients c j to obtain a more robust ODF estimation. The detailed implementation of the Laplace-Beltrami regularization and the comparison with the state of the art methods [5, 32] are presented in [22, 23].
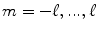 ), we define a modified SH basis that is real and symmetric. For even order ℓ, we define a single index j in terms of ℓ and m such that
), we define a modified SH basis that is real and symmetric. For even order ℓ, we define a single index j in terms of ℓ and m such that 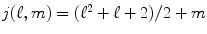 . The modified basis is given by
. The modified basis is given by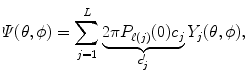
(3)
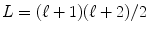 is the number of elements in the spherical harmonic basis, c j are the SH coefficients describing the input HARDI signal, P ℓ(j) is the Legendre polynomial of order ℓ(j)2 and c′ j the coefficients describing the ODF Ψ. Here, we estimate the c j coefficients with the solution presented in [23] with a Laplace-Beltrami regularization of the SH coefficients c j to obtain a more robust ODF estimation. The detailed implementation of the Laplace-Beltrami regularization and the comparison with the state of the art methods [5, 32] are presented in [22, 23].
is the number of elements in the spherical harmonic basis, c j are the SH coefficients describing the input HARDI signal, P ℓ(j) is the Legendre polynomial of order ℓ(j)2 and c′ j the coefficients describing the ODF Ψ. Here, we estimate the c j coefficients with the solution presented in [23] with a Laplace-Beltrami regularization of the SH coefficients c j to obtain a more robust ODF estimation. The detailed implementation of the Laplace-Beltrami regularization and the comparison with the state of the art methods [5, 32] are presented in [22, 23].3.1 Fibre ODF reconstruction
The relation between the measured diffusion ODF and the underlying fibre distribution, the fibre ODF, is still an important open question in the field [56, 65]. The diffusion ODF is a blurred version of the “true” fibre ODF. Because of this blurring effect, the extracted maxima of the diffusion ODF are often used for fibre tractography. An alternative is to use spherical deconvolution methods that provide an estimate of the fibre ODF [5, 20, 25, 37, 40, 58, 63, 64]. These techniques have better angular resolution than QBI and produce sharper fibre ODF profiles than the q-ball diffusion ODF. Smaller fibre compartments with smaller volume fractions are visible with fibre ODF and not with the diffusion ODF. SD and fibre ODF estimation are currently subject to active research. Here, we use a simple linear transformation of our analytical QBI solution. A schematic view of our spherical deconvolution method is shown in Fig. 2.
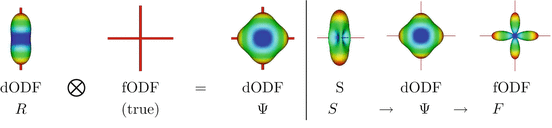

Fig. 2
Left: The convolution between the diffusion ODF kernel, R, and true fibre ODF produces a smooth diffusion ODF estimate, Ψ. Right: The Funk-Radon transform of the HARDI signal, S, produces a smooth diffusion ODF, Ψ, which is transformed into a sharper fibre ODF estimate, F, by the deconvolution
The fibre ODF is reconstructed in three steps. 1) The regularized diffusion ODF coefficients c′ j are reconstructed using Eq. (3) of the last section, 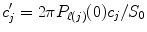 , where S 0 is the unweighted b = 0 diffusion image.
, where S 0 is the unweighted b = 0 diffusion image.
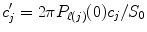 , where S 0 is the unweighted b = 0 diffusion image.
, where S 0 is the unweighted b = 0 diffusion image.2) The single fibre diffusion ODF, R, used as deconvolution kernel is estimated from the real data. As in [5, 64], we assume an axially symmetric diffusion tensor model with eigenvalues 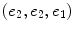 and e 1 > > e 2 for the underlying single fibre diffusion model. The values of e 1 and e 2 are estimated from 300 voxels with highest FA value in our real dataset, as these voxels can each be assumed to contain a single fibre population. The single fibre diffusion ODF kernel has an analytical expression [25] and is given by
and e 1 > > e 2 for the underlying single fibre diffusion model. The values of e 1 and e 2 are estimated from 300 voxels with highest FA value in our real dataset, as these voxels can each be assumed to contain a single fibre population. The single fibre diffusion ODF kernel has an analytical expression [25] and is given by
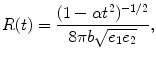
where 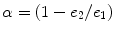 , b is the b-value of the real dataset and t ∈ [−1, 1] is the variable that represents the dot product between the direction of the fibre and the point of evaluation (θ, ϕ) on the sphere.
, b is the b-value of the real dataset and t ∈ [−1, 1] is the variable that represents the dot product between the direction of the fibre and the point of evaluation (θ, ϕ) on the sphere.
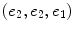 and e 1 > > e 2 for the underlying single fibre diffusion model. The values of e 1 and e 2 are estimated from 300 voxels with highest FA value in our real dataset, as these voxels can each be assumed to contain a single fibre population. The single fibre diffusion ODF kernel has an analytical expression [25] and is given by
and e 1 > > e 2 for the underlying single fibre diffusion model. The values of e 1 and e 2 are estimated from 300 voxels with highest FA value in our real dataset, as these voxels can each be assumed to contain a single fibre population. The single fibre diffusion ODF kernel has an analytical expression [25] and is given by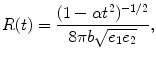
(4)
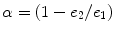 , b is the b-value of the real dataset and t ∈ [−1, 1] is the variable that represents the dot product between the direction of the fibre and the point of evaluation (θ, ϕ) on the sphere.
, b is the b-value of the real dataset and t ∈ [−1, 1] is the variable that represents the dot product between the direction of the fibre and the point of evaluation (θ, ϕ) on the sphere.3) The SH coefficient of the fiber ODF, f j , are then obtained by a simple linear transformation,
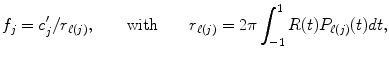
which can be solved analytically by taking the power expansion of P ℓ(j)(t) and integrating r ℓ(j) term by term. As for the analytical diffusion ODF solution, the spherical deconvolution is obtained with the Funk-Hecke theorem [23]. Therefore, the fibre ODF in terms of the HARDI signal is
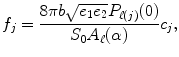
where 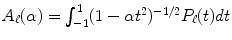 . The final fibre ODF is reconstructed for any (θ, ϕ) and point p as
. The final fibre ODF is reconstructed for any (θ, ϕ) and point p as 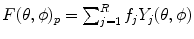 . In [25], the fibre ODF is shown to be a valid choice of fibre ODF that is in close agreement with the classical SD method [64].
. In [25], the fibre ODF is shown to be a valid choice of fibre ODF that is in close agreement with the classical SD method [64].
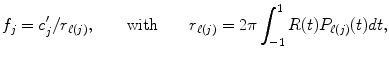
(5)
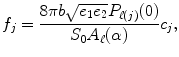
(6)
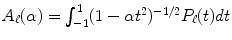 . The final fibre ODF is reconstructed for any (θ, ϕ) and point p as
. The final fibre ODF is reconstructed for any (θ, ϕ) and point p as 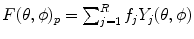 . In [25], the fibre ODF is shown to be a valid choice of fibre ODF that is in close agreement with the classical SD method [64].
. In [25], the fibre ODF is shown to be a valid choice of fibre ODF that is in close agreement with the classical SD method [64].4 Q-Ball Tractography
4.1 Deterministic Tractography
We extend the classical streamline techniques [9, 19, 50] based on diffusion tensor principal direction to take into account multiple fibre ODF maxima at each step. We denote p(s) as the curve parameterized by its arc-length. This curve can be computed as a 3D path adapting its tangent orientation locally according to vector field v. Hence, for a given starting point p 0, we solve 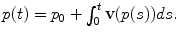 The integration is typically performed numerically with Euler or Runge-Kutta schemes of order 2 or 4. In the Euler case, we have the discrete evolution equation
The integration is typically performed numerically with Euler or Runge-Kutta schemes of order 2 or 4. In the Euler case, we have the discrete evolution equation
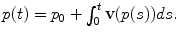 The integration is typically performed numerically with Euler or Runge-Kutta schemes of order 2 or 4. In the Euler case, we have the discrete evolution equation
The integration is typically performed numerically with Euler or Runge-Kutta schemes of order 2 or 4. In the Euler case, we have the discrete evolution equation