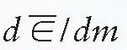 where
where 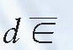 is the mean energy imparted by ionizing radiation to material of mass dm (1). The old unit of dose is rad (an acronym for radiation absorbed dose) and represents the absorption of 100 ergs of energy per gram of absorbing material:
is the mean energy imparted by ionizing radiation to material of mass dm (1). The old unit of dose is rad (an acronym for radiation absorbed dose) and represents the absorption of 100 ergs of energy per gram of absorbing material:

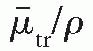 is the mass energy transfer coefficient for the medium averaged over the energy fluence spectrum of photons. As discussed in Section 5.4,
is the mass energy transfer coefficient for the medium averaged over the energy fluence spectrum of photons. As discussed in Section 5.4,
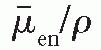 /ρ is the averaged mass energy absorption coefficient and
/ρ is the averaged mass energy absorption coefficient and 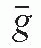 is the average fraction of an electron energy lost to radiative processes. Therefore,
is the average fraction of an electron energy lost to radiative processes. Therefore,


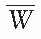 = 33.97 eV/ion pair (2). If e is the electronic charge (= 1.602 × 10-19 C), then
= 33.97 eV/ion pair (2). If e is the electronic charge (= 1.602 × 10-19 C), then 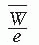 is the average energy required per unit charge of ionization produced. Since 1 eV = 1.602 × 10-19 J,
is the average energy required per unit charge of ionization produced. Since 1 eV = 1.602 × 10-19 J, 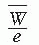 = 33.97 J/C. Exposure (X) is given by
= 33.97 J/C. Exposure (X) is given by



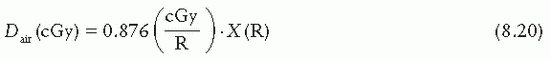
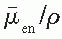 :
:

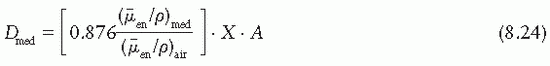

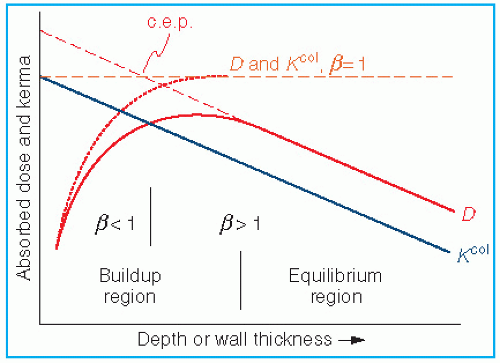
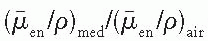 varies slowly with photon energy (˜10% variation from 10 keV and 10 MeV), the f factor for these materials does not vary much over practically the whole therapeutic range of energies. However, bone with a high effective atomic number not only has a much larger f factor between 10 and 100 keV, but also the f factor drops sharply from its maximum value of 4.24 at 30 keV to about 1.0 at 175 keV. This high peak value and rapid drop of the f factor are the result of the photoelectric process for which the mass energy absorption coefficient varies approximately as Z3 and 1/E3 (see Chapter 5). At higher photon energies where the Compton process is the predominant mode of interaction, the f factors are approximately the same for all materials.
varies slowly with photon energy (˜10% variation from 10 keV and 10 MeV), the f factor for these materials does not vary much over practically the whole therapeutic range of energies. However, bone with a high effective atomic number not only has a much larger f factor between 10 and 100 keV, but also the f factor drops sharply from its maximum value of 4.24 at 30 keV to about 1.0 at 175 keV. This high peak value and rapid drop of the f factor are the result of the photoelectric process for which the mass energy absorption coefficient varies approximately as Z3 and 1/E3 (see Chapter 5). At higher photon energies where the Compton process is the predominant mode of interaction, the f factors are approximately the same for all materials.in free air in the absence of the chamber (Fig. 8.2B). In other words, the perturbing influence of the chamber is removed once the chamber calibration factor is applied.
TABLE 8.1 f Factors for Water, Bone, and Muscle under Conditions of Charged Particle Equilibrium | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
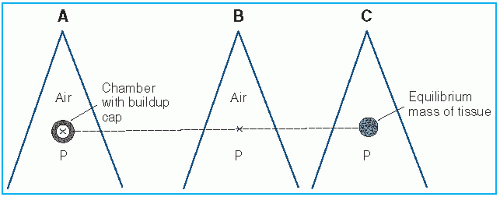 Figure 8.2. A: Chamber with buildup cap is placed in a radiation beam at point P in air and reading M is obtained. B: Exposure in free air at P is calculated using Equation 8.27. C: Dose in free space at P is calculated using Equation 8.28. |
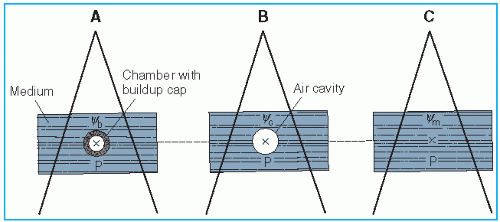 Figure 8.3. A: Chamber with buildup cap with its center at point P in a medium, exposed to a photon beam whose energy fluence is Ψb at P. Reading M is obtained. B: Exposure at P in air cavity of size equal to the external dimensions of the buildup cap is calculated. Energy fluence at P is Ψc. C: Absorbed dose at point P in the medium is calculated by Equation 8.29. Ψm is the energy fluence at P. |
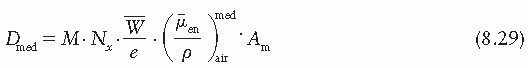
where electronic equilibrium does not exist. In addition, the term exposure applies only to x and γ radiations and for that reason methods of Section 8.3 are not valid for particle dosimetry. The Bragg-Gray cavity theory, on the other hand, may be used without such restrictions to calculate dose directly from ion chamber measurements in a medium.

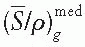 is a weighted mean ratio of the mass stopping power of the medium to that of the gas for the electrons crossing the cavity. The product of Jg (
is a weighted mean ratio of the mass stopping power of the medium to that of the gas for the electrons crossing the cavity. The product of Jg (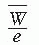 ) is the energy absorbed per unit mass of the cavity gas.
) is the energy absorbed per unit mass of the cavity gas.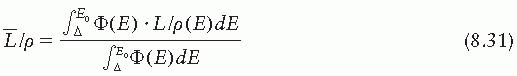

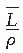 is the average restricted mass collisional stopping power of electrons. Tables A.1, A.2, A.3, A.4 and A.5 in the Appendix give
is the average restricted mass collisional stopping power of electrons. Tables A.1, A.2, A.3, A.4 and A.5 in the Appendix give 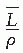 for various media and various photon and electron energies.
for various media and various photon and electron energies.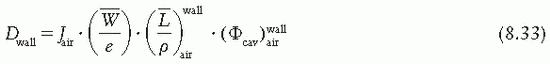
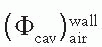 is the ratio of electron fluence at the reference point P (center of the cavity) with chamber cavity filled with wall material to that with the cavity filled with air. This correction is applied to the Bragg-Gray relation (Equation 8.29) to account for change in electron fluence.
is the ratio of electron fluence at the reference point P (center of the cavity) with chamber cavity filled with wall material to that with the cavity filled with air. This correction is applied to the Bragg-Gray relation (Equation 8.29) to account for change in electron fluence.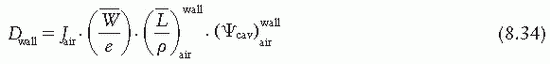
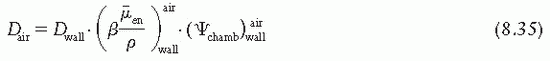
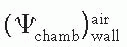 is the ratio that corrects for the change in photon energy fluence when air replaces the chamber (wall plus cap).
is the ratio that corrects for the change in photon energy fluence when air replaces the chamber (wall plus cap).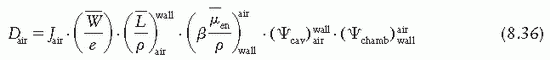
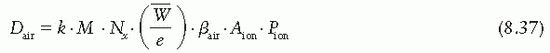
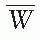 with humidity) is used by the NIST, which can be assumed constant in the relative humidity range of 10% to 90% for the measurement conditions with minimal error (19). Thus, the user does not need to apply additional humidity correction as long as it is used for dry air.
with humidity) is used by the NIST, which can be assumed constant in the relative humidity range of 10% to 90% for the measurement conditions with minimal error (19). Thus, the user does not need to apply additional humidity correction as long as it is used for dry air.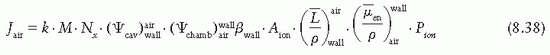
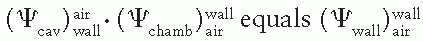 , which represents a correction for the change in Jair due to attenuation and scattering of photons in the chamber wall and buildup cap. This factor has been designated as Awall in the American Association of Physicists in Medicine (AAPM) protocol (6). Thus, Equation 8.38 becomes
, which represents a correction for the change in Jair due to attenuation and scattering of photons in the chamber wall and buildup cap. This factor has been designated as Awall in the American Association of Physicists in Medicine (AAPM) protocol (6). Thus, Equation 8.38 becomes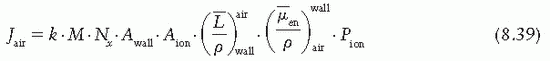
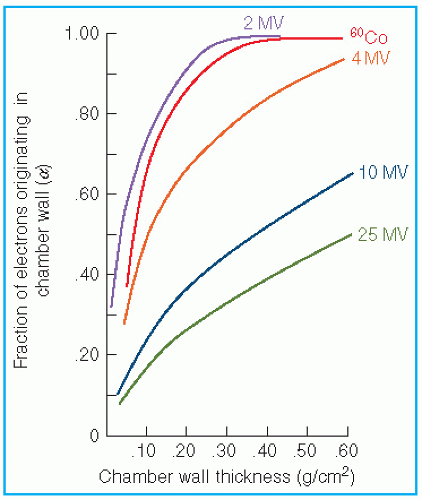
the fraction of cavity air ionization owing to electrons generated in the wall and the remaining (1 – α) from the buildup cap. Equation 8.39 can now be written as

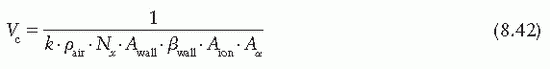
point of measurement is at a distance X above the center. Considering electrons entering the chamber at point A, the effective point of measurement is influenced by the number of electrons entering through a surface area ds at A of the chamber and the track length of these electrons in the cavity. Thus, the effective point of measurement, Xeff, can be determined by weighting the displacement X by the number of electrons (Φ · ds cos θ) entering the chamber and the track length (2X):
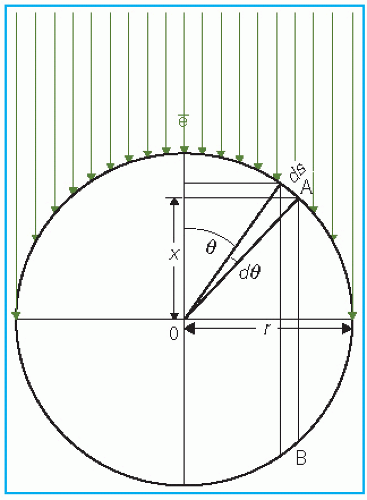 Figure 8.5. Diagram to illustrate the determination of effective point of measurement for a cylindrical chamber exposed to a unidirectional electron beam. |
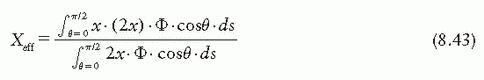
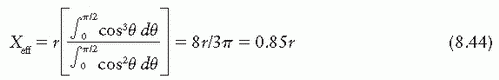
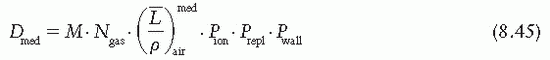
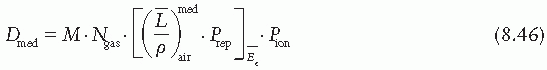
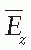 is the mean energy of the electron beam and Prepl is a replacement correction factor to account for three effects: (a) the in-scatter effect, which increases the fluence in the cavity since electron scattering out of the cavity is less than that expected in the intact medium; (b) the obliquity effect, which decreases the fluence in the cavity because electrons travel relatively straight in the cavity instead of taking oblique paths as they would owing to larger-angle scattering in the medium; and (c) displacement in the effective point of measurement, which gives rise to a correction if the point of measurement is on the sloping part of the depth-dose curve.
is the mean energy of the electron beam and Prepl is a replacement correction factor to account for three effects: (a) the in-scatter effect, which increases the fluence in the cavity since electron scattering out of the cavity is less than that expected in the intact medium; (b) the obliquity effect, which decreases the fluence in the cavity because electrons travel relatively straight in the cavity instead of taking oblique paths as they would owing to larger-angle scattering in the medium; and (c) displacement in the effective point of measurement, which gives rise to a correction if the point of measurement is on the sloping part of the depth-dose curve.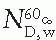 , instead of exposure or air kerma calibration of the ion chamber; (b) the user does not need to calculate any theoretical dosimetry factors; and (c) large tables of stopping-power ratios and mass energy absorption coefficients are not needed. Although the adoption of TG-51 results in only modest improvement in dosimetric accuracy over the TG-21 protocol (1% to 2%), the gain in simplicity is a significant factor from the user’s point of view.
, instead of exposure or air kerma calibration of the ion chamber; (b) the user does not need to calculate any theoretical dosimetry factors; and (c) large tables of stopping-power ratios and mass energy absorption coefficients are not needed. Although the adoption of TG-51 results in only modest improvement in dosimetric accuracy over the TG-21 protocol (1% to 2%), the gain in simplicity is a significant factor from the user’s point of view.Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree