Measurement of Ionizing Radiation
6.1. Introduction
In the early days of x-ray usage for diagnosis and therapy, attempts were made to measure ionizing radiation on the basis of chemical and biologic effects. For instance, radiation effects on photographic emulsions, changes in the color of some chemical compounds, and reddening of the human skin could be related to the amount of radiation absorbed. However, these effects were poorly understood at the time and could only provide crude estimation of radiation dose. For example, in radiotherapy, a unit called skin erythema dose (SED) was defined as that amount of x or γ radiation that just produced reddening of the human skin. However, the unit has many drawbacks. Skin erythema depends on many conditions, such as the type of skin, the quality of radiation, the extent of skin exposed, dose fractionation (dose per fraction and interval between fractions), and differences between early and delayed skin reactions.
Although the SED was later discarded in favor of a more precisely measurable unit such as the roentgen, the skin erythema was used by physicians as an approximate index of response to the radiation treatments. This happened in the orthovoltage era when the skin was the limiting organ to the delivery of tumoricidal doses. The reliance on skin reaction for the assessment of radiation response had to be abandoned when megavoltage beams with the skin-sparing properties became the main tools of radiation therapy.
In 1928, the International Commission on Radiation Units and Measurements (ICRU) adopted the roentgen as the unit of measuring x- and γ-radiation exposure. The unit is denoted by R.
6.2. The Roentgen
The roentgen is a unit of exposure. The quantity exposure is a measure of ionization produced in air by photons. The ICRU (1) defines exposure (X) as the quotient of dQ by dm where dQ is the absolute value of the total charge of the ions of one sign produced in air when all the electrons (negatrons and positrons) liberated by photons in air of mass dm are completely stopped in air.
The SI unit for exposure is coulomb per kilogram (C/kg), but the special unit is roentgen (R).1
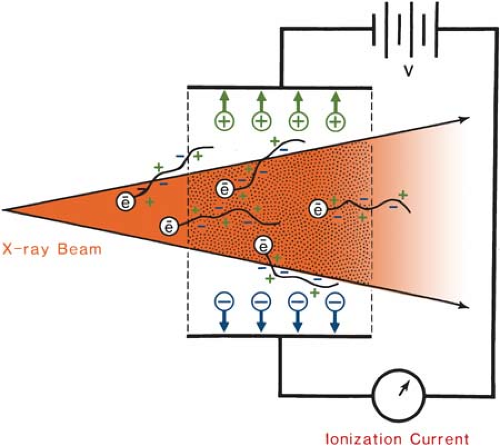
The definition of roentgen is illustrated in Figure 6.1. An x-ray beam in passing through air sets in motion electrons by photoelectric effect, Compton effect, or pair production. These high-speed electrons produce ionization along their tracks. Because of the electric field produced by the voltage applied across the ion-collection plates, the positive charges move toward the negative plate
and the negative charges move toward the positive plate. This constitutes a current. The collected charge of either sign can be measured by an electrometer.
and the negative charges move toward the positive plate. This constitutes a current. The collected charge of either sign can be measured by an electrometer.
According to the definition of roentgen, the electrons produced by photons in a specified volume (shaded in Fig. 6.1) must spend all their energies by ionization in air enclosed by the plates (region of ion collection) and the total ionic charge of either sign should be measured. However, some electrons produced in the specified volume deposit their energy outside the region of ion collection and thus are not measured. On the other hand, electrons produced outside the specified volume may enter the ion-collecting region and produce ionization there. If the ionization loss is compensated by the ionization gained, a condition of electronic equilibrium exists. Under this condition, the definition of roentgen is effectively satisfied. This is the principle of the free-air ionization chamber, described below.
6.3. Free-Air Ionization Chamber
The free-air, or standard, ionization chamber is an instrument used in the measurement of the roentgen according to its definition. Generally, such a primary standard is used only for the calibration of secondary instruments designed for field use. The free-air chamber installations are thus confined principally to some of the national standards laboratories.
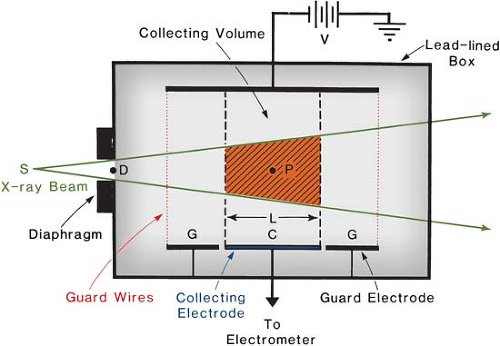
A free-air chamber is represented schematically in Figure 6.2. An x-ray beam, originating from a focal spot S, is defined by the diaphragm D, and passes centrally between a pair of parallel plates. A high-voltage (field strength of the order of 100 V/cm) is applied between the plates to collect ions produced in the air between the plates. The ionization is measured for a length L defined by the limiting lines of force to the edges of the collection plate C. The lines of force are made straight and perpendicular to the collector by a guard ring G.
As discussed previously, electrons produced by the photon beam in the specified volume (shaded in Fig. 6.2) must spend all their energy by ionization of air between the plates. Such a condition can exist only if the range of the electrons liberated by the incident photons is less than the distance between each plate and the specified volume. In addition, for electronic equilibrium to exist, the beam intensity (photon fluence per unit time) must remain constant across the length of the specified volume, and the separation between the diaphragm and the ion-collecting region must exceed the electron range in air.
If ΔQ is the charge collected in Coulombs and r is the density (kg/m3) of air, then the exposure Xp at the center of the specified volume (point P) is:
where Ap is the cross-sectional area (in meters squared) of the beam at point P and L (in meters) is the length of the collecting volume. In practice, it is more convenient to state the exposure (X) at the position of the diaphragm. Suppose φ1 and φ2 are the distances of the x-ray source to the diaphragm and point P, respectively. Because the intensity at point P and at the diaphragm are related by an inverse square law factor (φ1/φ2)2, which also relates the area of the beams at the diaphragm and at point P, exposure XD at the diaphragm is given by:
where AD is the diaphragm aperture area.
Accurate measurements with a free-air ionization chamber require considerable care. A few corrections that are usually applied include (a) correction for air attenuation; (b) correction for recombination of ions; (c) correction for the effects of temperature, pressure, and humidity on the density of air; and (d) correction for ionization produced by scattered photons. For details of various corrections the reader is referred to National Bureau of Standards handbook (2).
There are limitations on the design of a free-air chamber for the measurement of roentgens for high-energy x-ray beams. As the photon energy increases, the range of the electrons liberated in air increases rapidly. This necessitates an increase in the separation of the plates to maintain electronic equilibrium. Too large a separation, however, creates problems of nonuniform electric field and greater ion recombination. Although the plate separation can be reduced by using air at high pressures, the problems still remain in regard to air attenuation, photon scatter, and reduction in the efficiency of ion collection. Because of these problems, there is an upper limit on the photon energy above which the roentgen cannot be accurately measured. This limit occurs at about 3 MeV.
6.4. Thimble Chambers
Free-air ionization chambers are too delicate and bulky for routine use. Their main function is in the standardizing laboratories where they can be used to calibrate field instruments such as a thimble chamber.
The principle of the thimble chamber is illustrated in Figure 6.3. In Figure 6.3A, a spherical volume of air is shown with an air cavity at the center. Suppose this sphere of air is irradiated uniformly with a photon beam. Also, suppose that the distance between the outer sphere and the inner cavity is equal to the maximum range of electrons generated in air. If the number of electrons entering the cavity is the same as that leaving the cavity, electronic equilibrium exists. Suppose also that we are able to measure the ionization charge produced in the cavity by the electrons liberated in the air surrounding the cavity. Then, by knowing the volume or mass of air inside the cavity, we can calculate the charge per unit mass or the beam exposure at the center of the cavity. Now if the air wall in Figure 6.3A is compressed into a solid shell as in Figure 6.3B, we get a thimble chamber. Although the thimble wall is solid, it is air equivalent (i.e., its effective atomic number is the same as
that of air). In addition, the thickness of the thimble wall is such that the electronic equilibrium occurs inside the cavity, just as it did in Figure 6.3A. As before, it follows that the wall thickness must be equal to or greater than the maximum range of the electrons liberated in the thimble wall.
that of air). In addition, the thickness of the thimble wall is such that the electronic equilibrium occurs inside the cavity, just as it did in Figure 6.3A. As before, it follows that the wall thickness must be equal to or greater than the maximum range of the electrons liberated in the thimble wall.
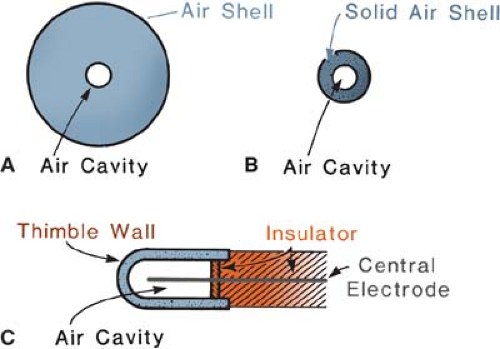 Figure 6.3. Schematic diagram illustrating the nature of the thimble ionization chamber. A: Air shell with air cavity. B: Solid air shell with air cavity. C: The thimble chamber. |
Since the density of the solid air-equivalent wall is much greater than that of free air, the thicknesses required for electronic equilibrium in the thimble chamber are considerably reduced. For example, in the 100- to 250-kVp x-ray range, the wall thickness of the thimble (assuming unit density) is about 1 mm, and in the case of 60Co γ rays (average hν ≈ 1.25 MeV), it is approximately 5 mm. In practice, however, a thimble chamber is constructed with wall thicknesses of 1 mm or less and this is supplemented with close-fitting caps of Plexiglas or other plastic to bring the total wall thickness up to that needed for electronic equilibrium for the radiation in question.
A. Chamber Wall
Figure 6.3C shows a typical thimble ionization chamber. The wall is shaped like a sewing thimble—hence the name. The inner surface of the thimble wall is coated by a special material to make it electrically conducting. This forms one electrode. The other electrode is a rod of low-atomic-number material such as graphite or aluminum held in the center of the thimble but electrically insulated from it. A suitable voltage is applied between the two electrodes to collect the ions produced in the air cavity.
As mentioned previously, most of the ionization produced in the cavity air arises from electrons liberated in the surrounding wall (for at least up to 2 MeV photons). For the thimble chamber to be equivalent to a free-air chamber, the thimble wall should be air equivalent. This condition would ensure that the energy spectrum of electrons liberated in the thimble wall is similar to that in air.
For the thimble chamber to be air equivalent, the effective atomic number of the wall material and the central electrode must be such that the system as a whole behaves like a free-air chamber. Most commonly used wall materials are made either of graphite (carbon), Bakelite, or a plastic coated on the inside by a conducting layer of graphite or of a conducting mixture of Bakelite and graphite. The effective atomic number of the wall is generally a little less than that of air. It is closer to that of carbon (Z = 6). As a consequence, such a wall should give rise to less ionization in the air cavity than a free-air wall. However, the usually greater atomic number of the central electrode, its dimensions, and the placement geometry within the thimble can provide compensation for the lower atomic number of the wall.
B. Effective Atomic Number
It is instructive to discuss the term effective atomic number (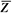 ) in greater detail. ) in greater detail. 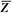 is the atomic number of an element with which photons interact the same way as with the given composite material. Since photoelectric effect is highly Z dependent (section 5.7), is the atomic number of an element with which photons interact the same way as with the given composite material. Since photoelectric effect is highly Z dependent (section 5.7), 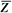 is considered for photoelectric interactions. Mayneord (3) has defined the effective atomic number of a compound as follows: is considered for photoelectric interactions. Mayneord (3) has defined the effective atomic number of a compound as follows: |
where α1, α2, α3, … an are the fractional contributions of each element to the total number of electrons in the mixture.
Example 1. Calculation of 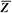 for Air for Air |
Composition by weight: nitrogen 75.5%, oxygen 23.2%, and argon 1.3%
Number of electrons/g of air: 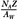 × (fraction by weight) × (fraction by weight) |

Total number of electrons/g of air = 3.01 × 1023 (Table 5.1)
C. Chamber Calibration
A thimble chamber could be used directly to measure exposure if (a) it were air equivalent, (b) its cavity volume were accurately known, and (c) its wall thickness was sufficient to provide electronic equilibrium. Under the above conditions, the exposure X is given by:
where Q is the ionization charge liberated in the cavity air of density r and volume v; A is the fraction of the energy fluence transmitted through the air-equivalent wall of equilibrium thickness. The factor A is slightly less than 1.00 and is used here to calculate the exposure for the energy fluence that would exist at the point of measurement in the absence of the chamber.
There are practical difficulties in designing a chamber that would rigorously satisfy the conditions of Equation 6.5. It is almost impossible to construct a thimble chamber that is exactly air equivalent, although with a proper combination of wall material and the central electrode one can achieve acceptable air equivalence in a limited photon energy range. In addition, it is difficult to determine accurately the chamber volume directly. Therefore, in actual practice, the thimble chambers are always calibrated against a free-air chamber for x-rays up to a few hundred kilovolts (2). At higher energies (up to 60Co γ rays), the thimble chambers are calibrated against a standard cavity chamber with nearly air-equivalent walls (e.g., graphite) and accurately known volume (4). In any case, the exposure calibration of a thimble chamber removes the need for knowing its cavity volume (see Chapter 8).
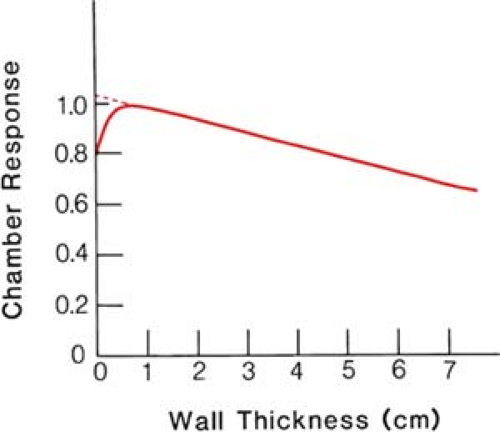
Although adequate wall thickness is necessary to achieve electronic equilibrium, the wall produces some attenuation of the photon flux. Figure 6.4 shows the effect of wall thickness on the chamber response. When the wall thickness is much less than that required for equilibrium or maximum ionization, too few electrons are generated in the wall, and thus the chamber response is low. Beyond the equilibrium thickness, the chamber response is again reduced because of increased attenuation of the beam in the wall. The true exposure (without attenuation) can be obtained by extrapolating linearly the attenuation curve beyond the maximum back to zero thickness, as shown in Figure 6.4. If the chamber response is normalized to the maximum reading, then the extrapolated
value for zero wall thickness gives the correction factor 1/A used in Equation 6.5. The correction for zero wall thickness, however, is usually allowed for in the exposure calibration of the chamber and is inherent in the calibration factor. Thus, when the calibration factor is applied to the chamber reading (corrected for changes in temperature and pressure of cavity air), it converts the value into true exposure in free air (without chamber). The exposure value thus obtained is free from the wall attenuation or the perturbing influence of the chamber.
value for zero wall thickness gives the correction factor 1/A used in Equation 6.5. The correction for zero wall thickness, however, is usually allowed for in the exposure calibration of the chamber and is inherent in the calibration factor. Thus, when the calibration factor is applied to the chamber reading (corrected for changes in temperature and pressure of cavity air), it converts the value into true exposure in free air (without chamber). The exposure value thus obtained is free from the wall attenuation or the perturbing influence of the chamber.
D. Desirable Chamber Characteristics
A practical ion chamber for exposure measurement should have the following characteristics:
There should be minimal variation in sensitivity or exposure calibration factor over a wide range of photon energies.
There should be suitable volume to allow measurements for the expected range of exposures. The sensitivity (charge measured per roentgen) is directly proportional to the chamber-sensitive volume. For example, the reading obtained for a given exposure with a 30-cm3 chamber will be approximately 50 times higher than that obtained with a 0.6-cm3 chamber. However, the ratio may not be exactly 50, because a chamber response also depends on the chamber design, as discussed previously.
There should be minimal variation in sensitivity with the direction of incident radiation. Although this kind of variation can be minimized in the design of the chamber, care is taken to use the chamber in the same configuration with respect to the beam as specified under chamber calibration conditions.
There should be minimal stem “leakage.” A chamber is known to have stem leakage if it records ionization produced anywhere other than its sensitive volume. The problem of stem leakage is discussed later in this chapter.
The chamber should have been calibrated for exposure against a standard instrument for all radiation qualities of interest.
There should be minimal ion recombination losses. If the chamber voltage is not high enough or regions of low electric field strength occur inside the chamber, such as in the vicinity of sharply concave surfaces or corners, ions may recombine before contributing to the measured charge. The problem becomes severe with high-intensity or pulsed beams.
6.5. Practical Thimble Chambers
A. Condenser Chambers
A condenser chamber is a thimble ionization chamber connected to a condenser. Figure 6.5 shows a Victoreen condenser chamber, manufactured by Victoreen Instrument Company. The thimble at the right-hand end consists of an approximately air-equivalent wall (Bakelite, nylon, or other composition) with a layer of carbon coated on the inside to make it electrically conducting. The conducting layer makes contact with the metal stem. The central electrode (aluminum rod) is connected to a conducting layer of carbon coated on the inside of a hollow polystyrene insulator. This arrangement of an outer metal shield and an inner conducting layer with an insulator in between constitutes an electrical condenser capable of storing charge. The central wire and the thimble’s inner conducting surface together also act as a condenser. Thus, the chamber has a total capacitance (C) between the central electrode and the outer metal sheath, which is given by:
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree