the spatial domain (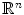 in the continuous case or
in the continuous case or 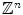 in the discrete case). Fuzzy sets can be considered from two points of view. In the first one, a membership function is a function μ from the space
in the discrete case). Fuzzy sets can be considered from two points of view. In the first one, a membership function is a function μ from the space 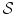 on which the image is defined into [0, 1]. The value μ(x) is the membership degree of x (
on which the image is defined into [0, 1]. The value μ(x) is the membership degree of x (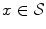 ) to a spatial fuzzy object. In the second one, a membership function is defined as a function μ′ from a space of attributes
) to a spatial fuzzy object. In the second one, a membership function is defined as a function μ′ from a space of attributes 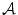 into [0, 1]. At numerical level, such attributes are typically the grey levels. The value μ′(g) represents the degree to which a grey level g supports the membership to an object or a class. There is an obvious relation between μ and μ′ in grey level based processing: μ(x) = μ′[g(x)], where g(x) denotes the grey level of x in the considered image.
into [0, 1]. At numerical level, such attributes are typically the grey levels. The value μ′(g) represents the degree to which a grey level g supports the membership to an object or a class. There is an obvious relation between μ and μ′ in grey level based processing: μ(x) = μ′[g(x)], where g(x) denotes the grey level of x in the considered image.
Such models explicitly represent imprecision in the information provided by the images, as well as possible ambiguity between classes. For instance the problem of partial volume effect finds a consistent representation in this model. A pixel or voxel suffering from partial volume effect is characterized by its partial belonging to two (or more) different tissues or classes, i.e. by non zero membership values to several classes. Figure
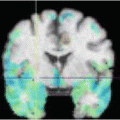
1 shows an example of an MR image of the brain of a patient suffering from adrenoleukodystrophy, and where the slice thickness induces a high partial volume effect. The grey levels on the right figure represent the membership values to the pathology. The pathology is then considered as a fuzzy object, represented by a membership function defined on the spatial domain.
More generally, a spatial fuzzy object may represent different types of imprecision, either on the boundary of the objects (due for instance to partial volume effect, or to the spatial resolution), or on the individual variability of these structures, etc.
There is no definite answer to the question of how defining the membership functions. As mentioned above, they can be directly derived from the grey levels, but other characteristics can be used as well. For instance the contours of an object can be defined as a fuzzy set with a membership function depending on the gradient intensity. Based on a detection operator of some specific objects, the membership functions can be derived from the magnitude of the answer provided by this operator. Imprecision can also be introduced from a first crisp estimation of the objects, typically at their boundary as a function of the distance to the crisp object, to account for imprecision in this estimation. Finally, several approaches rely on fuzzy classification methods to derive membership functions.
2.2 Fuzzy classification
Learning of membership functions is a difficult task that still does not have a definite answer. Several methods have been proposed in the literature, often based on the minimization of some criteria. Among these methods, the most used is the fuzzy C-means algorithm (FCM) [
5]. The idea is to define a membership function of a point to each class (which is then a fuzzy set), instead of deriving crisp assignments.
The FCM algorithm iteratively modifies a fuzzy partition so as to minimize an objective function defined as:
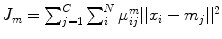
, under the constraint that
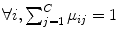
, where
C denotes the number of class,
N the number of points to be classified,
μ i j the membership function of point
i to class
j, and
m is a parameter belonging to ]1, +
∞[ called fuzzy factor, which controls the amount of “fuzziness” of the classification. The membership function is deduced from the cluster center position as:
![$$\mu _{ij} = \frac{1} {\sum _{j=1}^{C}[ \frac{\vert \vert x_{i}-m_{i}\vert \vert } {\vert \vert x_{i}-m_{j}\vert \vert )} ]^{ \frac{2} {m-1} }}$$](/wp-content/uploads/2016/09/A151032_1_En_2_Chapter_IEq9.gif)
, and the cluster center position is obtained by:
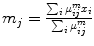
. From an initialization of cluster centers, the membership values and cluster centers are alternatively updated using these two equations, until convergence. Convergence towards a local minimum of the objective function has been proved. An example is provided in Fig.
2, in the case of a 1-dimensional 2-class problem. It also illustrates one of the main drawbacks of this approach: the membership functions are not decreasing with respect to the distance to the cluster center. This is due to the normalization constraint, and this phenomenon gets even worse with more classes.
An alternative solution to fuzzy C-means classification, which avoids the normalization drawbacks, is given by possibilistic C-means (PCM) [
40]. The objective functional is defined as:
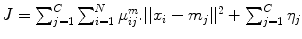
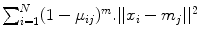
and the obtained membership function is:
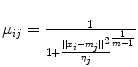
. Now the membership functions are decreasing with respect to the distance to the class centers. However this algorithm is very sensitive to initialization and sometimes coincident clusters may occur.
To address the problems of FCM and PCM a new fuzzy possibilistic C-mean (FPCM) algorithm was proposed in [
49] by combining these two algorithms. The objective function involves both membership and typicality. FPCM solves the noise sensitivity defect of FCM and overcomes the problem of coincident clusters of PCM. Although FPCM is less prone to the problems of FCM and PCM, in the case of a large data set this algorithm does not work properly since the typicality values are very small in such cases, again due to a normalization constraint. This constraint has been suppressed in possibilistic fuzzy c-mean (PFCM) [
50]. Recently, approaches have been proposed by modifying the objective function to increase the robustness of FCM to noise [
1,
33,
44,
45,
59,
64]. They also try to incorporate spatial information, by defining membership functions that depend on a local neighborhood around each point.
Another class of methods relies on probability-possibility transformations [
29,
31,
39]. Other methods based on statistical information have been proposed, also by minimizing some criteria (e.g. [
23,
25]). However, most criteria provide a function that depends on the shape of the histogram. Accounting for frequent situations where a pixel may belong completely and without any ambiguity to a class while having a grey-level with low occurrence frequency thus becomes difficult.
In [
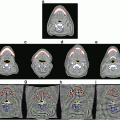
13] an original approach was proposed to obtain membership values from grey-level histogram. Two types of criteria are used simultaneously. The first type is based on a “resemblance” between the grey-level histogram and the membership function in the form of a distance between the two distributions. This type is very close to existing methods. The second type accounts for prior information on the expected shape of the membership function, in order to deal with problems mentioned above concerning low occurrence frequencies. This calls for a parametric representation of the functions. The combination of these two types of criteria leads to a simpler interpretation of the obtained functions that fits better the intuitive notion of membership. Membership functions are chosen as simple trapezoidal functions, whose parameters are estimated (simultaneously for all class membership functions) using simulated annealing in order to optimize the two criteria. The results obtained on a MR brain image are illustrated in Fig.
3. This method has been applied successfully to several problems like multi-image classification or segmentation of internal brain structures.
Finally, other types of classification methods, such as k-nearest neighbors, have also been extended to the fuzzy case.
Despite their drawbacks, these methods are quite widely used, mostly as an initialization for further more sophisticated processing. For instance, an adaptive C-means algorithm was used in [
69] in order to take the partial volume effect into account in a deformable model approach. An original fuzzy classification method taking spatial context into account was also used as the initialization of a deformable model in [
38] for segmenting brain tumors of different types, shapes and locations in 3D MRI. Some results are shown in Sect.
6.
2.3 Local operations for filtering or edge detection
In this section, we summarize the main techniques for local filtering in a broad sense, aiming at enhancing the contrast of an image, at suppressing noise, at extracting contours, etc. Note that these aims are different and often contradicting each other. However, the principles of the techniques are similar, and they can be grouped into two classes: techniques based on functional optimization on the one hand, and rule based techniques on the other hand. These aspects have been largely developed in the literature (see e.g. [
2,
6,
42,
67]), and we provide here just the main lines.
Functional approaches consist in minimizing or maximizing a functional, which can be interpreted as an analytical representation of some objective. For instance, enhancing the contrast of an image according to this technique amounts to reduce the fuzziness of the image. This can be performed by a simple modification of membership functions (for instance using intensification operators), by minimizing a fuzziness index such as entropy, or even by determining an optimal threshold value (for instance optimal in the sense of minimizing a fuzziness index) which provides an extreme enhancement (until binarization) [
51,
52].
Other methods consist in modifying classical filters (median filter for instance) by incorporating fuzzy weighting functions [
43].
Rule based techniques rely on ideal models (of filters, contours, etc.). These ideal cases being rare, variations and differences with respect to these models are permitted through fuzzy representations of the models, as fuzzy rules. For instance, a smoothing operator can be expressed by [
62,
63]:
IF |
a pixel is darker than its neighbors |
THEN |
increase its grey level |
ELSE IF |
the pixel is lighter than its neighbors |
THEN |
decrease its grey level |
OTHERWISE |
keep it unchanged |
In this representation, the emphasized terms are defined by fuzzy sets or fuzzy operations. Typically, the grey level characteristics are defined by linguistic variables, the semantics of which are provided by fuzzy sets on the grey level interval. Actions are fuzzy functions applied on grey levels and on pixels. The implementation of these fuzzy rules follows the general principles of fuzzy logic [
30].
More complex rules can be found, for instance in [
41,
56], where a contour detector is expressed by a set of rules involving the gradient, the symmetry and the stiffness of the contour. Fuzzy rule based systems have also been proposed for contour linking, based on proximity and alignment criteria.
Note that rules are sometimes but a different representation of functional approaches. Their main advantage is that they are easy to design (in particular for adaptive operators) and to interpret, and they facilitate the communication with the user.
3 Intermediate level
Several operations have been defined in the literature on fuzzy objects, in particular spatial fuzzy objects, since the early works of Zadeh [
71] on set operations, and of Rosenfeld on geometrical operations [
60].
Typical examples of geometrical operations are area and perimeter of a fuzzy object. They can be defined as crisp numbers, where the computation involves each point up to its degree of membership. But since objects are not well defined, it can also be convenient to consider that measures performed on them are imprecise too. This point of view leads to definitions as fuzzy numbers [
30].
Such geometrical measures can typically be used in shape recognition, where geometrical attributes of the objects are taken into account.
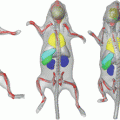
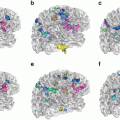
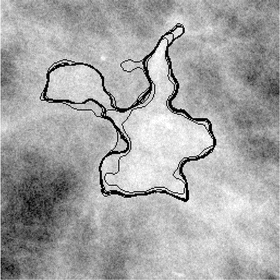
As an example, fuzzy measures have been used in [
58] for detecting masses in digital breast tomosynthesis. The measures are performed on detected fuzzy regions, that are considered as candidate particles (Fig.
4). A decision concerning their recognition is performed by combining fuzzy attributes. Fuzzy decision trees can be used to this aim [
20,
53].
It has been shown in [
65,
66] that using fuzzy representations of digital objects allow deriving more robust measures than using crisp representations, and in particular dealing properly with the imprecision induced by the digitization process.
Such measures can also be used as descriptors for indexation and data mining applications.
Let us now consider topological features and the example of fuzzy connectivity. The degree of connectivity between two points
x and
y in a fuzzy object
μ in a finite discrete space is defined as [
60]:
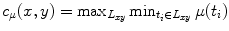
, where
L x y is any path from
x to
y. This definition was exploited in fuzzy connectedness notions [
68], now widely used in medical image segmentation and incorporated in freely available softwares such as ITK
1.
Morphological operations have also been defined on fuzzy objects (see e.g. [
17]). We give here general definitions, for fuzzy erosion and dilation, from which several other morphological operations can be derived:
In these equations,
μ denotes the fuzzy set to be dilated or eroded,
ν the fuzzy structuring element,
t a conorm (fuzzy intersection),
T the t-conorm (fuzzy union) associated to
t with respect to the complementation
c.
Such fuzzy morphological operations have been used in medical imaging for instance for taking into account the spatial imprecision on the location of vessel walls for 3D reconstruction of blood vessels by fusing angiographic and ultrasonic acquisitions [
19]. They also constitute a good formal framework for defining fuzzy spatial relations, as will be seen in Sect.
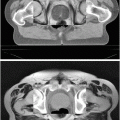
4. Another application of fuzzy morphology is for defining median fuzzy sets and series of interpolating fuzzy sets [
12], which can typically be used for representing variability based on several instances of an anatomical structures or for atlas construction. An example is illustrated in Fig.
5.
Some approaches using fuzzy rules can also be found at intermediate level. Let us just mention two examples. The first one [
28] deals with the segmentation of osseous surface in ultrasound images. It uses fuzzy representations of image intensity and gradient, as well as their fusion, in rules that mimic the reasoning process of a medical expert and that include knowledge about the physics of ultrasound imaging. This approach was successfully tested on a large image data set.
The second example is completely different and fuzzy rules are used in [
24] to tune the parameters of a deformable model for segmenting internal structures of the brain. This approach elegantly solves the difficult problem of parameter tuning in such segmentation methods, and proved to provide very good results on normal cases.
4 Higher level
The main information contained in the images consists of properties of the objects and of relations between objects, both being used for pattern recognition and scene interpretation purposes. Relations between objects are particularly important since they carry structural information about the scene, by specifying the spatial arrangements between objects. These relations highly support structural recognition based on models. This models can be of iconic type, as an anatomical atlas, or of symbolic type, as linguistic descriptions or ontologies. Although the use of iconic representations for normal structure recognition is well acknowledged, they remain difficult to exploit in pathological cases. Anatomical knowledge is also available in textbooks or dedicated web sites, and is expressed mainly in linguistic form. These models involve concepts that correspond to anatomical objects, their characteristics, or the spatial relations between them. Human experts use intensively such concepts and knowledge to recognize visually anatomical structures in images. This motivates their use in computer aided image interpretation. Some attempts to formalize this knowledge has been recently performed, in particular in the form of ontologies (e.g. the Foundational Model of Anatomy [
61]).
In our work, we concentrate mainly on spatial relations, which are strongly involved in linguistic descriptions. They constitute a very important information to guide the recognition of structures embedded in a complex environment, and are more stable and less prone to variability (even in pathological cases) than object characteristics such as shape or size. We proposed mathematical models of several spatial relations (adjacency, distances, directional relations, symmetry, between…) [
8–
10,
15,
18,
27], in the framework of fuzzy sets theory, which proved useful to recognize thoracic and brain structures [
14,
16,
26]. These fuzzy representations can enrich anatomical ontologies and contribute to fill the semantic gap between symbolic concepts, as expressed in the ontology, and visual percepts, as extracted from the images. These ideas were used in particular in our segmentation and recognition methods [
3,
36]: a concept of the ontology is used for guiding the recognition by expressing its semantics as a fuzzy set, for instance in the image domain or in an attribute domain, which can therefore be directly linked to image information.
The methods we develop in our group for segmentation and recognition of 3D structures in medical images can be seen as spatial reasoning processes. Two main components of this domain are spatial knowledge representation and reasoning. In particular spatial relations constitute an important part of the knowledge we have to handle, as explained before. Imprecision is often attached to spatial reasoning in images, and can occur at different levels, from knowledge to the type of question we want to answer. The reasoning component includes fusion of heterogeneous spatial knowledge, decision making, inference, recognition. Two types of questions are raised when dealing with spatial relations:
Get Clinical Tree app for offline access

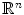 in the continuous case or
in the continuous case or 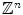 in the discrete case). Fuzzy sets can be considered from two points of view. In the first one, a membership function is a function μ from the space
in the discrete case). Fuzzy sets can be considered from two points of view. In the first one, a membership function is a function μ from the space 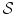 on which the image is defined into [0, 1]. The value μ(x) is the membership degree of x (
on which the image is defined into [0, 1]. The value μ(x) is the membership degree of x (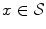 ) to a spatial fuzzy object. In the second one, a membership function is defined as a function μ′ from a space of attributes
) to a spatial fuzzy object. In the second one, a membership function is defined as a function μ′ from a space of attributes 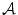 into [0, 1]. At numerical level, such attributes are typically the grey levels. The value μ′(g) represents the degree to which a grey level g supports the membership to an object or a class. There is an obvious relation between μ and μ′ in grey level based processing: μ(x) = μ′[g(x)], where g(x) denotes the grey level of x in the considered image.
into [0, 1]. At numerical level, such attributes are typically the grey levels. The value μ′(g) represents the degree to which a grey level g supports the membership to an object or a class. There is an obvious relation between μ and μ′ in grey level based processing: μ(x) = μ′[g(x)], where g(x) denotes the grey level of x in the considered image.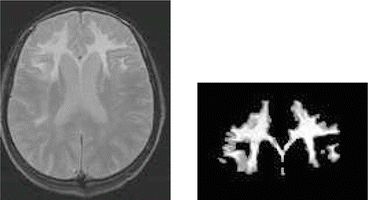
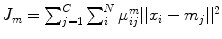 , under the constraint that
, under the constraint that 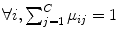 , where C denotes the number of class, N the number of points to be classified, μ i j the membership function of point i to class j, and m is a parameter belonging to ]1, +∞[ called fuzzy factor, which controls the amount of “fuzziness” of the classification. The membership function is deduced from the cluster center position as:
, where C denotes the number of class, N the number of points to be classified, μ i j the membership function of point i to class j, and m is a parameter belonging to ]1, +∞[ called fuzzy factor, which controls the amount of “fuzziness” of the classification. The membership function is deduced from the cluster center position as: ![$$\mu _{ij} = \frac{1} {\sum _{j=1}^{C}[ \frac{\vert \vert x_{i}-m_{i}\vert \vert } {\vert \vert x_{i}-m_{j}\vert \vert )} ]^{ \frac{2} {m-1} }}$$](/wp-content/uploads/2016/09/A151032_1_En_2_Chapter_IEq9.gif) , and the cluster center position is obtained by:
, and the cluster center position is obtained by: 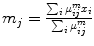 . From an initialization of cluster centers, the membership values and cluster centers are alternatively updated using these two equations, until convergence. Convergence towards a local minimum of the objective function has been proved. An example is provided in Fig. 2, in the case of a 1-dimensional 2-class problem. It also illustrates one of the main drawbacks of this approach: the membership functions are not decreasing with respect to the distance to the cluster center. This is due to the normalization constraint, and this phenomenon gets even worse with more classes.
. From an initialization of cluster centers, the membership values and cluster centers are alternatively updated using these two equations, until convergence. Convergence towards a local minimum of the objective function has been proved. An example is provided in Fig. 2, in the case of a 1-dimensional 2-class problem. It also illustrates one of the main drawbacks of this approach: the membership functions are not decreasing with respect to the distance to the cluster center. This is due to the normalization constraint, and this phenomenon gets even worse with more classes.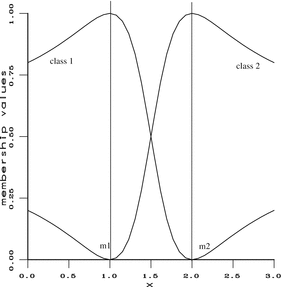
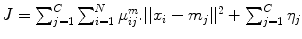
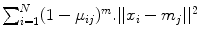 and the obtained membership function is:
and the obtained membership function is: 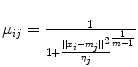 . Now the membership functions are decreasing with respect to the distance to the class centers. However this algorithm is very sensitive to initialization and sometimes coincident clusters may occur.
. Now the membership functions are decreasing with respect to the distance to the class centers. However this algorithm is very sensitive to initialization and sometimes coincident clusters may occur.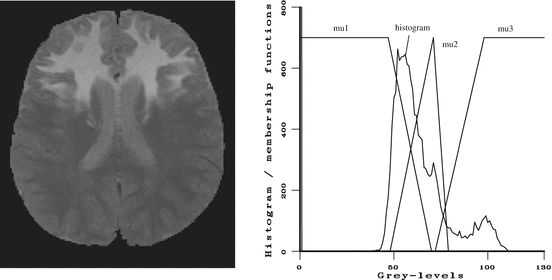
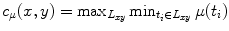 , where L x y is any path from x to y. This definition was exploited in fuzzy connectedness notions [68], now widely used in medical image segmentation and incorporated in freely available softwares such as ITK1.
, where L x y is any path from x to y. This definition was exploited in fuzzy connectedness notions [68], now widely used in medical image segmentation and incorporated in freely available softwares such as ITK1.![$$\displaystyle{ \forall x \in \mathcal{S},\;E_{\nu }(\mu )(x) =\inf _{y\in \mathcal{S}}T[c(\nu (y - x)),\mu (y)], }$$](/wp-content/uploads/2016/09/A151032_1_En_2_Chapter_Equ1.gif)
![$$\displaystyle{ \forall x \in \mathcal{S},\;D_{\nu }(\mu )(x) =\sup _{y\in \mathcal{S}}t[\nu (x - y),\mu (y)]. }$$](/wp-content/uploads/2016/09/A151032_1_En_2_Chapter_Equ2.gif)