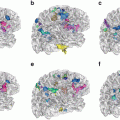
Fig. 1
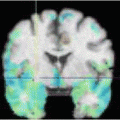
a) Subcortical structures have a spherical topology. For instance, the shape of the hippocampus can be continuously deformed onto a sphere. b) The human cerebral cortex is a highly folded ribbon of gray matter that lies inside the cerebrospinal fluid (the red interface) and outside the white matter of the brain (the green interface). When the midline connections between the left and right hemisphere are artificially closed, these two surfaces have the topology of a sphere. c) Due to the partial volume effect, subject motion, etc…, it becomes hard to distinguish opposite banks of a the gray matter. d) Segmentation algorithms that do not constrain the topology often produce cortical segmentations with several topological defects (i.e. handles, cavities, disconnected components). e) A close-up of a topologically-incorrect cortical surface representation
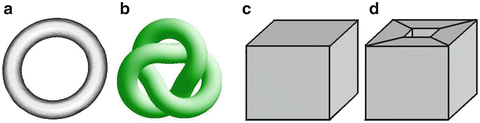
Fig. 2
a-b) Two tori that are homeomorphically equivalent. They share the same intrinsic topology. However, they do not share the same homotopy type as one cannot be continuously transformed into the other. c) A geometric object with a spherical topology; its Euler-characteristic is 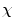 = v − e + f = 8 − 12 + 6 = 2. d) A geometric object with a toroidal topology and an Euler-characteristic of
= v − e + f = 8 − 12 + 6 = 2. d) A geometric object with a toroidal topology and an Euler-characteristic of 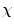 = v − e + f = 16 − 32 + 16 = 0
= v − e + f = 16 − 32 + 16 = 0
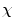 = v − e + f = 8 − 12 + 6 = 2. d) A geometric object with a toroidal topology and an Euler-characteristic of
= v − e + f = 8 − 12 + 6 = 2. d) A geometric object with a toroidal topology and an Euler-characteristic of 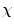 = v − e + f = 16 − 32 + 16 = 0
= v − e + f = 16 − 32 + 16 = 0Although many clinical and research applications require accurate segmentations that respect the true anatomy of the targeted structures, only a few techniques have been proposed to achieve accurate and topologically-correct segmentations.
1.2 Motivation
Many neurodegenerative disorders, psychiatric disorders, and healthy aging are frequently associated with structural changes in the brain. These changes, which can cause alterations in the imaging properties of the brain tissue, as well as in morphometric properties of brain structures, can be captured and detected by sophisticated segmentation techniques. Certain clinical and research applications depend crucially on the accuracy and correctness of the representations (visualization [11, 12, 56], spherical coordinate system and surface-based atlases [12, 16–18, 22, 50, 56], shape analysis [16, 20, 31, 43, 53, 54], surface-based processing of functional data [12], and inter-subject registration [22, 51, 55], among others). Small geometric errors in a segmentation can easily change the apparent connectivity of the segmented structure, posing a problem to studies that aim at analyzing the connectedness of different regions (e.g. dramatic underestimation of true geodesic distances). The accuracy and correctness of the representations can be critical factors in the success of studies investigating the subtle early effects of various disease processes.
1.3 Challenges
Accurate segmentation under anatomical consistency is challenging. Segmentation algorithms, which operate on the intensity or texture variations of the image, are sensitive to the artifacts produced by the image acquisition process. These limitations include image noise, low frequency image intensity variations or non-uniformity due to radio frequency (RF) inhomogeneities, geometric distortions in the images, partial volume averaging effect, and subject motion. Segmentation techniques that do not integrate any topological constraints generate segmentations that often contain deviations from the true topology of the structures of interest. These deviations are called topological defects and can be of three types: cavities, disconnected components, or handles (which are topologically equivalent to holes) that incorrectly connect parts of the volumes.
The integration of topological constraints significantly increases the complexity of the task. Topology is both a global and a local concept; small and local modifications of a geometric shape can change its global connectivity. Furthermore, topology is intrinsically a continuous concept (Sect. 2.1) and topological notions are difficult to adapt into a discrete framework (Sect. 2.2). Due to these difficulties, the set of techniques applicable to the segmentation of images is quite limited (Sect. 3).
In this chapter, we present background material of central importance for the segmentation of medical images under topological constraints. We introduce some elementary notions of topology (Sect. 2.1) and show how these notions can be adapted into a discrete framework and applied to the segmentation problem (Sect. 2.2). Next, we describe the current state-of- the-art segmentation of images under topological constraints (Sect. 3) and detail the limitations of existing approaches (Sect. 3). Section 4 concludes.
2 Topology in Medical Imaging
In medical image segmentation, one is interested in locating (accurately and also under topological constraints) specific regions of interest that are formed by one or several anatomical structures. Those can be represented equivalently by their volume or their surface and these two equivalent representations correspond to the two most common data structures used in medical imaging: 3D voxel grids and surfaces (such as triangulations or levelsets).
2.1 General Notions of Topology
Topology is a branch of mathematics that studies the properties of geometric figures by abstracting their inherent connectivity while ignoring their detailed form. The exact geometry of the objects, their location and the details of their shape are irrelevant to the study of their topological properties. Schematically, this amounts to characterizing a geometric object (i.e. a surface or a volume) by its number of disconnected components, holes and cavities, but not by their position. For instance, the surface of a coffee mug with a handle has the same topology as the surface of a doughnut (this type of surface is called a one-handled torus).
A – Homeomorphism, Genus, and Euler-Characteristic
In medical imaging, the geometric entities under consideration are anatomical structures, which can frequently be advantageously represented by their surfaces. The Gauss-Bonnet theorem in differential geometry links the geometry of surfaces with their topology. Any compact connected orientable surface is homeomorphic to a sphere with some number of handles. This number of handles is a topological invariant called the genus. For example, a sphere is of genus 0 and a torus is of genus 1. The genus g is directly related to another topological invariant called the Euler-characteristic 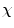 by the formula
by the formula 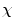 = 2(1 − g).2 The Euler-characteristic is of great practical interest because it can be calculated from any polyhedral decomposition (e.g. triangulation) of the surface by the simple formula
= 2(1 − g).2 The Euler-characteristic is of great practical interest because it can be calculated from any polyhedral decomposition (e.g. triangulation) of the surface by the simple formula 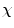 = v − e + f, where v, e and f denote respectively the number of vertices, edges and faces of the polyhedron. The Euler-characteristic of a sphere is
= v − e + f, where v, e and f denote respectively the number of vertices, edges and faces of the polyhedron. The Euler-characteristic of a sphere is 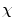 = 2. This implies that any surface with
= 2. This implies that any surface with 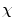 = 2 is topologically equivalent (i.e. homeomorphic) to a sphere and therefore does not contain any handles. Surfaces with an Euler-characteristic
= 2 is topologically equivalent (i.e. homeomorphic) to a sphere and therefore does not contain any handles. Surfaces with an Euler-characteristic 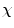 < 2 have a topology that is different from that of a sphere. Note, however, that the Euler-characteristic does not provide any information about the localization of the handles.
< 2 have a topology that is different from that of a sphere. Note, however, that the Euler-characteristic does not provide any information about the localization of the handles.
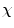 by the formula
by the formula 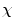 = 2(1 − g).2 The Euler-characteristic is of great practical interest because it can be calculated from any polyhedral decomposition (e.g. triangulation) of the surface by the simple formula
= 2(1 − g).2 The Euler-characteristic is of great practical interest because it can be calculated from any polyhedral decomposition (e.g. triangulation) of the surface by the simple formula 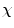 = v − e + f, where v, e and f denote respectively the number of vertices, edges and faces of the polyhedron. The Euler-characteristic of a sphere is
= v − e + f, where v, e and f denote respectively the number of vertices, edges and faces of the polyhedron. The Euler-characteristic of a sphere is 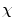 = 2. This implies that any surface with
= 2. This implies that any surface with 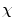 = 2 is topologically equivalent (i.e. homeomorphic) to a sphere and therefore does not contain any handles. Surfaces with an Euler-characteristic
= 2 is topologically equivalent (i.e. homeomorphic) to a sphere and therefore does not contain any handles. Surfaces with an Euler-characteristic 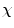 < 2 have a topology that is different from that of a sphere. Note, however, that the Euler-characteristic does not provide any information about the localization of the handles.
< 2 have a topology that is different from that of a sphere. Note, however, that the Euler-characteristic does not provide any information about the localization of the handles.B – Intrinsic Topology and Homotopy Type
Homeomorphisms are used to define the intrinsic topology of an object, independently of the embedding space. The topological invariance of the Euler characteristic implies that the way a surface is decomposed (i.e. tessellated) does not influence its (intrinsic) topology. Any polyhedral decomposition of a surface will encode the same intrinsic topology. For example, a knotted solid torus has the same genus (and the same Euler-characteristic 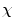 = 0) as a simple torus. In order to topologically differentiate surfaces, one needs a theory that considers the embedding space. Homotopy, which defines two surfaces to be homotopic if one can be continuously transformed into the other, is such a theory that provides a measure of an object’s topology (see [8] for an excellent course in algebraic topology). We stress the fact that the Euler-characteristic does not define the homotopy type of a surface, since the embedding space is being ignored. In particular, this implies that a discrete representation of a surface using a polygonal decomposition with the desired Euler-characteristic might be self-intersecting in the 3D embedding space (Fig 3).
= 0) as a simple torus. In order to topologically differentiate surfaces, one needs a theory that considers the embedding space. Homotopy, which defines two surfaces to be homotopic if one can be continuously transformed into the other, is such a theory that provides a measure of an object’s topology (see [8] for an excellent course in algebraic topology). We stress the fact that the Euler-characteristic does not define the homotopy type of a surface, since the embedding space is being ignored. In particular, this implies that a discrete representation of a surface using a polygonal decomposition with the desired Euler-characteristic might be self-intersecting in the 3D embedding space (Fig 3).
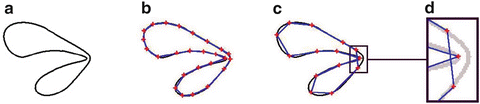
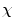 = 0) as a simple torus. In order to topologically differentiate surfaces, one needs a theory that considers the embedding space. Homotopy, which defines two surfaces to be homotopic if one can be continuously transformed into the other, is such a theory that provides a measure of an object’s topology (see [8] for an excellent course in algebraic topology). We stress the fact that the Euler-characteristic does not define the homotopy type of a surface, since the embedding space is being ignored. In particular, this implies that a discrete representation of a surface using a polygonal decomposition with the desired Euler-characteristic might be self-intersecting in the 3D embedding space (Fig 3).
= 0) as a simple torus. In order to topologically differentiate surfaces, one needs a theory that considers the embedding space. Homotopy, which defines two surfaces to be homotopic if one can be continuously transformed into the other, is such a theory that provides a measure of an object’s topology (see [8] for an excellent course in algebraic topology). We stress the fact that the Euler-characteristic does not define the homotopy type of a surface, since the embedding space is being ignored. In particular, this implies that a discrete representation of a surface using a polygonal decomposition with the desired Euler-characteristic might be self-intersecting in the 3D embedding space (Fig 3).
Fig. 3
a) a simple closed curve with the topology of a circle. b) One example of a polyhedral decomposition of the curve using 25 vertices and edges. The corresponding Euler-characteristic 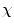 = v − e = 0 is that of a circle. c) Another discretization of the same curve using 14 edges and vertices. Note that the Euler-characteristic is still that of a circle
= v − e = 0 is that of a circle. c) Another discretization of the same curve using 14 edges and vertices. Note that the Euler-characteristic is still that of a circle 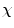 = 0, even though the discrete representation of the curve self-intersects in the 2D embedding space. d) Close-up
= 0, even though the discrete representation of the curve self-intersects in the 2D embedding space. d) Close-up
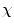 = v − e = 0 is that of a circle. c) Another discretization of the same curve using 14 edges and vertices. Note that the Euler-characteristic is still that of a circle
= v − e = 0 is that of a circle. c) Another discretization of the same curve using 14 edges and vertices. Note that the Euler-characteristic is still that of a circle 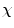 = 0, even though the discrete representation of the curve self-intersects in the 2D embedding space. d) Close-up
= 0, even though the discrete representation of the curve self-intersects in the 2D embedding space. d) Close-upC – Topological Defects, Duality Foreground/Background
In this chapter, we call topological defect any deviation from spherical topology: cavities, disconnected components, or handles. We note that for each defect present in a geometric entity, referred to as the foreground object, there exists a corresponding defect in the background (i.e. the embedding space): a disconnected foreground component can be interpreted as a background cavity; a foreground cavity is a disconnected background component; and a handle in a foreground component defines another handle in the background component. This foreground/background duality is of crucial importance for all retrospective topology correction techniques, as it provides a dual methodology to correct a topological defect. For instance, the presence of a handle in an object could be corrected by either cutting the handle in the foreground object, or cutting the corresponding handle in the background object. Cutting the background handle can be interpreted as filling the corresponding foreground hole (Fig. 4-b,c).
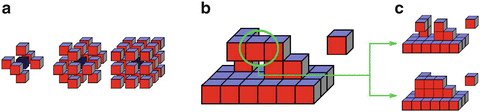

Fig. 4
a) 6-, 18- and 26-connectivity. b) The circled voxel is a non-simple point c) Several dual topological corrections are possible: either cutting the handle (top) or filling the hole (bottom)
2.2 Topology and Discrete Imaging
In order to apply topological concepts to a discrete framework and define the topology type (i.e. homotopy type) of digital segmentations, the notion of continuity must be adapted to discrete spaces and objects, such as 3D image grids and triangulations. This is obtained by replacing the notion of continuity with the weaker notion of connectivity. We describe how topological notions can be adapted to the two most common data structures used in medical imaging: 3D data structures and surfaces.
A – Digital Topology
Digital topology provides an elegant framework, which translates the continuous concepts of topology to discrete images. In this theory, binary images inherit a precise topological meaning. In particular, the concept of homotopic deformation, which is required to assign a topological type to a digital object, is clearly defined through the notion of simple point. An extensive discussion of these concepts can be found in [36]. In this section, some basic notions of digital topology are presented. All definitions are from the work of G. Bertrand, which we refer to for more details [7].
In the digital topology framework, a 3D image I is interpreted as a graph. The vertices of the graph are the digital points (i.e. the voxels) and the edges are defined through neighborhood relations between points (i.e. the connectivity). A 3D binary digital image I is composed of a foreground object X and its inverse, the complement. We first need to define the concept of connectivity, which specifies the condition of adjacency that two points must fulfill to be regarded as connected. Three types of connectivity are commonly used in 3D: 6-, 18- and 26-connectivity. Two voxels are 6-adjacent if they share a face, 18-adjacent if they share at least an edge and 26-adjacent if they share at least a corner (Fig. 4-a). In order to avoid topological paradoxes, different connectivities, n and 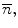 must be used for one digital object X and its complement
must be used for one digital object X and its complement 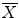 . This leaves us with four pairs of compatible connectivities: (6,26), (6,18), (26,6) and (18,6). One important consequence of the previous requirement is that digital topology does not provide a consistent framework for multi-label images. No compatible connectivities can be chosen for neighboring components of the same object. Therefore, digital topology is strictly limited to binary images.
. This leaves us with four pairs of compatible connectivities: (6,26), (6,18), (26,6) and (18,6). One important consequence of the previous requirement is that digital topology does not provide a consistent framework for multi-label images. No compatible connectivities can be chosen for neighboring components of the same object. Therefore, digital topology is strictly limited to binary images.
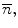 must be used for one digital object X and its complement
must be used for one digital object X and its complement 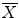 . This leaves us with four pairs of compatible connectivities: (6,26), (6,18), (26,6) and (18,6). One important consequence of the previous requirement is that digital topology does not provide a consistent framework for multi-label images. No compatible connectivities can be chosen for neighboring components of the same object. Therefore, digital topology is strictly limited to binary images.
. This leaves us with four pairs of compatible connectivities: (6,26), (6,18), (26,6) and (18,6). One important consequence of the previous requirement is that digital topology does not provide a consistent framework for multi-label images. No compatible connectivities can be chosen for neighboring components of the same object. Therefore, digital topology is strictly limited to binary images.We now come to the definition of a simple point. This concept is central to most digital segmentation methods that integrate topological constraints [3, 26, 32, 36, 42, 44, 49].
Definition 1.1 Simple point.
A point of a binary object is simple if it can be added or removed without changing the topology of both the object and the background, that is, without changing the number of connected components, cavities and handles of both X and 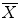 (Fig. 4 -b,c).
(Fig. 4 -b,c).
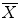 (Fig. 4 -b,c).
(Fig. 4 -b,c). A simple point is easily characterized by two topological numbers with respect to the digital object (X, 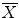 ) and a consistent connectivity pair (n,
) and a consistent connectivity pair (n, 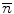 ). These numbers, denoted T n (x, X) and
). These numbers, denoted T n (x, X) and 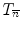 (x,
(x, 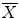 ), were introduced by G. Bertrand in [1] as an elegant way to classify the topology type of a given voxel. The values of T n (x, X) and
), were introduced by G. Bertrand in [1] as an elegant way to classify the topology type of a given voxel. The values of T n (x, X) and 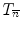 (x,
(x, 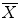 ) characterize isolated, interior and border points as well as different kinds of junctions. In particular, a point is simple if and only if T n (x, X) =
) characterize isolated, interior and border points as well as different kinds of junctions. In particular, a point is simple if and only if T n (x, X) = 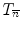 (x,
(x, 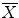 ) = 1. Their efficient computation, which only involves the 26-neighborhood, is described in [6].
) = 1. Their efficient computation, which only involves the 26-neighborhood, is described in [6].
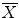 ) and a consistent connectivity pair (n,
) and a consistent connectivity pair (n, 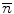 ). These numbers, denoted T n (x, X) and
). These numbers, denoted T n (x, X) and 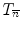 (x,
(x, 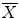 ), were introduced by G. Bertrand in [1] as an elegant way to classify the topology type of a given voxel. The values of T n (x, X) and
), were introduced by G. Bertrand in [1] as an elegant way to classify the topology type of a given voxel. The values of T n (x, X) and 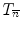 (x,
(x, 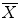 ) characterize isolated, interior and border points as well as different kinds of junctions. In particular, a point is simple if and only if T n (x, X) =
) characterize isolated, interior and border points as well as different kinds of junctions. In particular, a point is simple if and only if T n (x, X) = 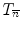 (x,
(x, 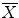 ) = 1. Their efficient computation, which only involves the 26-neighborhood, is described in [6].
) = 1. Their efficient computation, which only involves the 26-neighborhood, is described in [6].The definition of a discrete homotopy follows from the concept of simple point.
Definition 1.2 Homotopic deformation.
We define a homotopic deformation of an object X as a sequence of deletions or additions of simple points.
Finally, two objects X and Y share the same homotopy type if there exists a sequence of transformations X 0 …X k and a sequence of points x 1 … x k , such that X 0 = X and 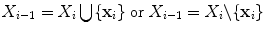 and the point x i is simple relative to X i for i = 1, …, k.
and the point x i is simple relative to X i for i = 1, …, k.
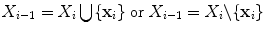 and the point x i is simple relative to X i for i = 1, …, k.
and the point x i is simple relative to X i for i = 1, …, k.To be complete, we also mention some recent research in digital topology, such as the concept of multisimple point in [45, 44] to characterize the modification of the genus, a novel characterization of homeomorphic deformation in [4], as well as some octree grid topology concept in [1].
B – Surfaces in Discrete Imaging
We now turn to the translation of continuous topological concepts to discrete surface representations. There are essentially two ways of representing a surface in discrete imaging. Surfaces can be either represented explicitly, by using a parameterized polygonal decomposition, or implicitly as the level set of some function defined in the 3D embedding space. Each type of representation has advantages and disadvantages, and has been extensively used for the purpose of medical image segmentation [11, 13, 21, 23, 35, 37, 57–59].
B.1 – Explicit Representations
An explicit representation models a surface by a set of vertices, edges, and faces, associated with a chosen parameterization of each face. The set of vertices, edges, and faces composes the polyhedral representation of the surface. The parameterization of the faces determines the exact geometry of the surface. For instance, tessellations correspond to linear parameterizations of each face, while splines use higher-order approximations. Triangulations are a special kind of tessellation, in which each face is a triangle (Fig. 5-a).
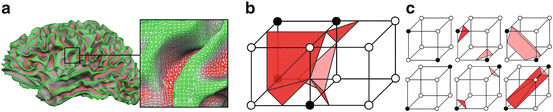

Fig. 5




a) A triangulated cortical surface b) Tiling inconscistency in isosurface extraction c) Different tessellations corresponding to different topology types
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree