Fig. 5.1
As sound energy moves through a medium, it causes compression and rarefaction of the molecules comprising the medium as depicted by the line drawing. This is expressed mathematically as a sine wave
The velocity of sound is equal to the frequency times the wavelength (v = fλ) (Fig. 5.2). Unlike light waves, the velocity of sound wave propagation is a property of the medium. Air, which is relatively low in density, has a relatively low sound velocity. Water and the various organs and soft tissues of the body, which are comprised primarily of water, have higher sound velocities. Very dense solids such as the bone have a much higher sound velocity. Ultrasound machines for medical imaging are calibrated for the velocity of sound waves in soft tissue. Sound waves that enter air (as in the trachea) or bone will not generate an interpretable echo because of the large difference in the timing of the echo (Table 5.1).
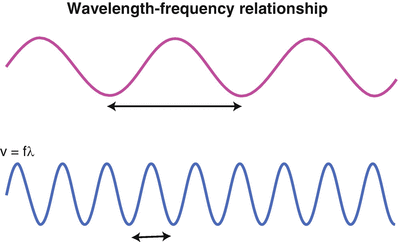

Fig. 5.2
Velocity (V, or often noted as c) = frequency (in cycles/second) × wavelength (λ, distance/cycle). For a given velocity (determined by the medium), a higher frequency is accompanied by a shorter wavelength . The top sine wave represents sound with a longer wavelength and lower frequency as compared with the bottom sine wave which depicts a higher frequency wave with shorter wavelength
Table 5.1
Velocity of sound in common materials in m/s
Air | 340 |
Water | 1500 |
Fata | 1470 |
Livera | 1540 |
Musclea | 1500–1600 |
Bonea | 1900–3700 |
Sound power is the amount of energy striking a point over a unit of time and is measured in Watts. Sound intensity is the measure of the amount of energy being transmitted through a given area and is expressed in Watts per meter squared. The threshold of human hearing is approximately 1 × 10−12 W/m2 and is defined as 0 decibel (dB). The decibel scale is logarithmic (dB = 10log(x)). Therefore, a doubling of sound intensity equals a dB change of approximately 3 (10log(2)). Sound intensity is related to pressure amplitude by the equation:
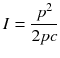 where p = pressure amplitude , ρ (rho) = density of the medium, and c = sound velocity. Therefore, doubling the pressure amplitude will quadruple the intensity.
where p = pressure amplitude , ρ (rho) = density of the medium, and c = sound velocity. Therefore, doubling the pressure amplitude will quadruple the intensity.
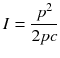
Sound intensity decreases with distance from the source according to the inverse square law . As the distance from the source increases, the sound intensity decreases by the distance squared. Therefore, doubling the distance will decrease the sound intensity by a factor of 4 (Fig. 5.3).
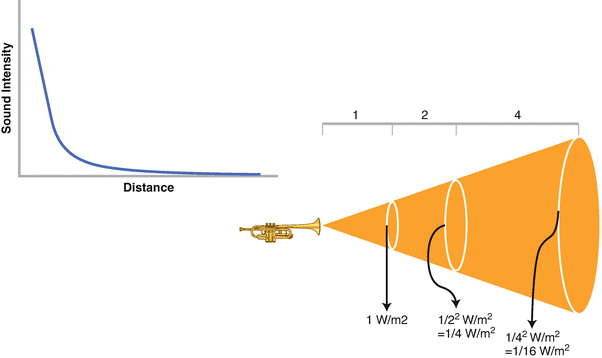

Fig. 5.3
The inverse square law . Sound intensity decreases exponentially as distance increases from the sound source. Sound intensity (y axis) decreases exponentially with distance from the source (x axis). As distance increases by a factor of 2 sound intensity decreases by a factor of 4
In medical ultrasound, sound power is a fundamental property of the sound wave transmitted from the ultrasound probe. Increasing sound power is similar to turning up the volume on a stereo and can be adjusted on the ultrasound unit. While imaging ultrasound operates well within the safe limits of power output, caution must still be used to avoid unnecessary energy delivery. Thermal injury due to heat transfer has not been reported with diagnostic ultrasound, though it remains a theoretical possibility [1). In practical application in neck ultrasound, sound power is rarely altered. If deep structures cannot be well imaged, increasing the gain or decreasing the frequency of the probe output will usually improve the image [see below).
The propagation of sound is highly influenced by certain characteristics of the medium or mediums through which it travels. Acoustical impedance is one of these and equals density times propagation speed (Z = ρv, where Z = impedance, ρ (rho) = density, and v = propagation speed.). Differences in acoustical impedance account for refraction and reflection at the interface between two media (see below). Another property of the medium that influences sound propagation is its viscosity which affects sound attenuation (a decrease in sound energy). Attenuation is dependent on the viscosity of the medium and the frequency squared of the sound wave and is described mathematically in Stokes’ law of sound attenuation:
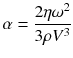 where η (eta) is the dynamic viscosity coefficient of the fluid, ω (omega) is the sound’s frequency , ρ (rho) is the fluid density, and V is the speed of sound in the medium [3]. Stokes’ law is an oversimplification in the case of medical ultrasound, but more complete description is beyond the scope of this text. Notice that the attenuation of sound (α) increases exponentially as frequency increases. This fact has important implications in understanding the limitations of high-frequency ultrasound probes for assessing structures deep within the body. Attenuation values [α (alpha)] have been determined empirically for a number of tissues and are typically expressed in dB/cm [4].
where η (eta) is the dynamic viscosity coefficient of the fluid, ω (omega) is the sound’s frequency , ρ (rho) is the fluid density, and V is the speed of sound in the medium [3]. Stokes’ law is an oversimplification in the case of medical ultrasound, but more complete description is beyond the scope of this text. Notice that the attenuation of sound (α) increases exponentially as frequency increases. This fact has important implications in understanding the limitations of high-frequency ultrasound probes for assessing structures deep within the body. Attenuation values [α (alpha)] have been determined empirically for a number of tissues and are typically expressed in dB/cm [4].
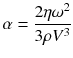
The effect of frequency in choice of medical ultrasound probes can be seen with a simple example. Calculation of attenuation over a given distance can be done by this simple equation:
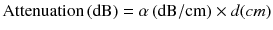 Using Stokes’ law we can see that doubling the frequency (ω (omega)) will increase α (alpha) by a factor of 4. In the above equation let’s compare the effects of doubling a probe frequency , from 5 to 10 MHz. If attenuation equals α for a 5 MHz probe, then attenuation for the 10 MHz probe will equal 4α (alpha). In other words, for any given distance from the probe, attenuation will be four times greater when probe frequency is doubled.
Using Stokes’ law we can see that doubling the frequency (ω (omega)) will increase α (alpha) by a factor of 4. In the above equation let’s compare the effects of doubling a probe frequency , from 5 to 10 MHz. If attenuation equals α for a 5 MHz probe, then attenuation for the 10 MHz probe will equal 4α (alpha). In other words, for any given distance from the probe, attenuation will be four times greater when probe frequency is doubled.
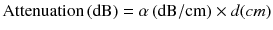
In summary we see that as distance increases away from a sound source, sound intensity decreases by the inverse square law . In addition attenuation causes exponential loss of sound energy, with losses occurring more rapidly for higher frequencies. So the sound-striking objects that are relatively distant from the source is of much lower intensity than that striking objects close to the source. Therefore, echoes coming from those distant sources are correspondingly weaker.
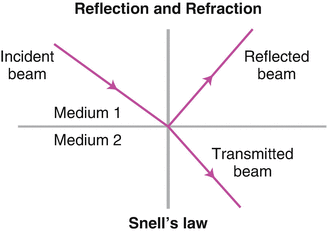
Echoes are the result of reflected sound energy returning to the probe and must be detected to provide imaging details of an object. Transmission of the sound waves is also necessary to penetrate into tissues that lie deeper in the body. As noted above, differences in acoustical impedance between media accounts for interfaces that both reflect and refract the sound waves according to Snell’s law (Fig. 5.4). When sound travels through soft tissues with relatively similar acoustic impendences, such as subcutaneous fat and muscle, some echoes are reflected back to the probe but much of the sound is transmitted deeper into the body, allowing imaging of the deeper tissues until eventually the sound beam is diminished to the point that echoes are inaudible to the probe. If sound travels through acoustically dissimilar tissues, such as air and subcutaneous fat, nearly all of the beam would be reflected back at the interface and very little would be transmitted. For this reason, acoustic coupling gel, a substance with acoustic properties similar to water, is applied to the skin surface when performing medical ultrasound. High-intensity echoes (from intense reflection) which appear bright white on the imaging screen are termed “echogenic,” whereas those which are poorly reflective appear darker. Reflectors can generally be described as a diffuse (reflecting echoes in many different directions, such as a bicycle reflector ) or specular (reflecting echoes primarily in a single direction, such as a mirror) [2]. Most tissues are diffuse reflectors.