Radiation and the Atom
2.0 INTRODUCTION
Radiation refers to energy that propagates through space or matter. Two important categories of radiation in medical imaging are electromagnetic radiation (EMR) and subatomic particulate radiation.
Diagnostic imaging began with the discovery of x-rays by German mechanical engineer and physicist Wilhelm C. Rontgen approximately 115 years ago. While the immense scope and enormous impact of this discovery could not have been imagined at the turn of the 19th century, the word of its discovery and early applications spread rapidly across the world, and Rontgen received the first Nobel Prize in Physics in 1901.
While other imaging modalities will be discussed, the x-ray, in its many embodiments (e.g., radiography, CT, fluoroscopy, mammography), is still the most common form of energy used in radiology.
With x-ray imaging, only a small fraction of the initial number of x-rays generated by the x-ray tube are transmitted toward the body, and only a small fraction of those (approximately 1%) exit and are recorded on an image receptor.
Even fewer photons are detected and localized to create images in diagnostic nuclear medicine. In contrast to x-ray imaging where the recorded signal has been transmitted through the body, photons used in nuclear medicine (mainly in the form of high-energy EMR, e.g., gamma [γ]-rays) are emitted from radiopharmaceuticals (pharmaceuticals, chemicals, or other substances labeled with radioactive materials) inside the body that were administered by inhalation, orally, or intravenously prior to imaging. The images created reveal the radiopharmaceutical’s biodistribution, thus providing diagnostic information to the radiologist.
Magnetic resonance imaging (MRI) utilizes strong magnetic fields and pulsed radiofrequency (RF) EMR to excite protons and to localize return signals, producing images which represent and are highly sensitive to the local variations in biochemical detail arising from differences the proton density and magnetic field properties of the different types of tissues that comprise internal organs (e.g., fat, water, muscle, gray matter).
2.1 CLASSICAL ELECTROMAGNETISM
1. Classical electrostatics: Branch of physics that studies the interactions between stationary electric charges using an extension of the classical Newtonian model.
2. Maxwell’s equations: Four widely used mathematical equations that describe how electric and magnetic fields propagate and interact, and how they are influenced by objects they encounter.
a. Established the foundation for fields such as special relativity and quantum mechanics.
3. Electron energy levels: One of the revelations to come out of quantum mechanics was the concept that a particle that is bound (confined spatially, like orbital electrons of an atom) can only have particular discrete values of energy.
a. Orbital electron binding energies describe the energy required to overcome the attractive force of the protons’ positive electric field and eject electrons from specific orbitals in atoms. The lowest energy level an electron can have in this bound state is -13.6 eV, meaning that at least 13.6 eV of energy would need to be transferred to the electron to liberate it from the atom. In general, energy levels can also refer to the state of the atomic nucleus or vibrational or rotational energy levels in molecules.
b. Energy units—In medical imaging, this energy is typically measured in multiples of electron volts (eV); 1 keV = 1,000 eV; 1 MeV = 1,000,000 eV
(i) The formal definition is 1 eV equals the kinetic energy acquired by an electron as it accelerates across an electrical potential difference (voltage) of one volt in a vacuum.
(ii) One eV is an incredibly small amount of energy. When you apply a force (F) to lift the 4th edition of our textbook (2.7 kg) by one foot (F = ma, where m is mass in kg and a is the acceleration due to gravity approximately 10 ms-2), you do work (W = Fd) of approximately: 2.7 kg × 10 ms-2 × 0.3 m = 8.1 J, which is about 5.1 × 1019 eV. However, as discussed in Chapter 3, if that same amount of energy were transferred to the book in the form of ionizing radiation, the dose of radiation the book would have received in Gray (Gy where 1 Gy = 1 J/kg) would be (8.1 J/2.7 kg) = 3 Gy. While not a lot of energy, it is a very large dose of radiation from a viewpoint of its potential for biological damage. As discussed in Chapter 20, if this dose were to be applied to the whole body at one time, the chance of survival would be approximately 50% in 30 days.
2.2 ELECTROMAGNETIC RADIATION
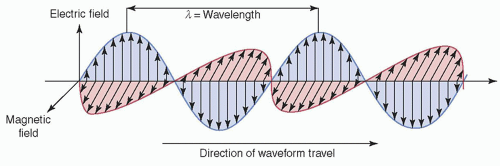
1. Electromagnetic radiation (EMR) is a traveling sinusoidal wave consisting of inseparable, self-sustaining oscillating electric and magnetic field components that propagate together at the speed of light (c) approximately 3.8 × 108 ms-1 in a vacuum (Fig. 2-1)
▪ FIGURE 2-1 Electric and magnetic field components of EM radiation. EMR propagates as a pair of oscillating and mutually reinforcing electric and magnetic fields that are orthogonal (perpendicular) to one another and to the direction of propagation.
F. 2-3.
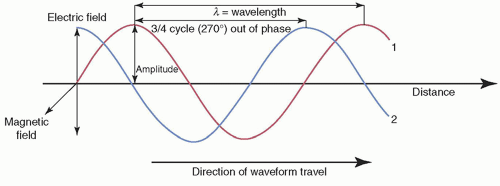
2. Wave characteristics of electromagnetic radiation (Fig. 2-2)
a. Wavelength (λ): distance between any two identical points on adjacent cycles (typically in nm)
b. Amplitude (A): maximal height or magnitude
c. Intensity (I): power/area, which is proportional to the square of the amplitude
d. Period (T): the time to complete one cycle of a wave (time for wave of λ to pass a fixed point)
e. Frequency(ν): number of periods that occur per second, inversely equal to the period: ν = 1/T. Measured in multiples of hertz (Hz); MHz—106, GHz—109, THz—1012
f. Energy (E): E = hν, where h is Planck’s constant (see Section 2.3.1)
g. Phase: temporal shift of one wave relative to another
h. Speed (c) of EMR: is constant in a given medium
(i) Frequency and wavelength are inversely proportional
(ii) Velocity (v) of EMR in a medium with a refractive index (n)
n for selected media: vacuum, n = 1.0; water @ 20°C, n = 1.33; olive oil, n = 1.46; diamond, n = 2.42
▪ FIGURE 2-2 Characterization of EM waves of equal wavelength and amplitude, but with wave #2 having a ¾ cycle phase difference.
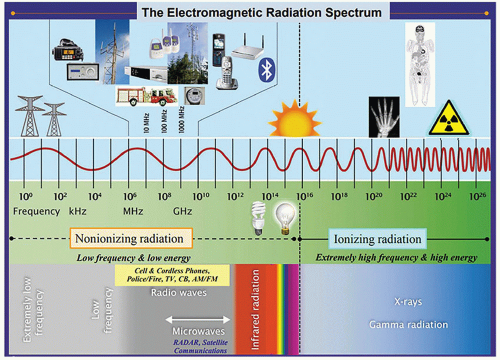
3. The electromagnetic radiation spectrum
a. EMR is commonly used at different frequencies for a wide variety of applications. Examples in order of increasing energy and frequency include radio waves, infrared waves, visible light, ultraviolet rays, x-rays, and gamma rays (Fig. 2-3).
(i) EMR can propagate through matter but does not require matter for its propagation.
(ii) EMR is emitted every time a charged particle accelerates.
(iii) EMR obeys the laws of optics at all frequencies, which include refraction, reflection, dispersion, interference, and diffraction.
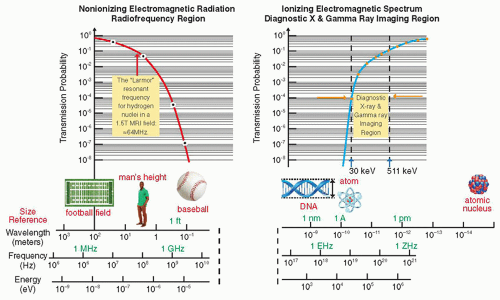
4. Penetration of electromagnetic radiation in tissue
a. The energy of the EMR must be able to penetrate and interact with the organ and tissue of interest to interrogate the physical or chemical structure of organs and tissues within the body through imaging with EMR (Fig. 2-4).
 ▪ FIGURE 2-3 The electromagnetic spectrum.  F. 2-1—(MODIFIED) |
 ▪ FIGURE 2-4 Attenuation of electromagnetic energy in the radiofrequency and diagnostic x- and γ-ray regions of the electromagnetic spectrum as it is transmitted through 25 cm of soft tissue. At low frequencies (low MRI), less attenuation takes place. At higher frequencies (where x- and γ-rays are used in medical imaging), frequencies and photon energies increase with the fraction of radiation transmitted. |
2.3 BEHAVIOR OF ENERGY AT THE ATOMIC SCALE: ONE OF THE MOST IMPORTANT DISCOVERIES IN THE HISTORY OF SCIENCE
1. Energy quanta and the photon: Max Planck ushered in the dawn of quantum mechanics with his suggestion that energy could only be emitted or absorbed in multiples of some minimal finite discrete packets of energy he called quanta (called the term photon in 1926), the smallest quantity of EMR.
a. Energy of a photon is given by
where Planck’s constant, h, = 6.626 × 10-34 J-s = 4.136 × 10-18 keV-s
b. When E is expressed in keV and λ in nanometers (nm)
2. Particle characteristics of electromagnetic radiation: In 1905, Albert Einstein postulated that Planck’s quanta were acting like physical particles—namely photons. This elucidation is now known as the photoelectric effect. Einstein was awarded the Nobel Prize in Physics in 1921 for this discovery.
3. Wave-particle duality (proposed in 1924 by future Nobel Laureate Louis de Broglie)
a. All particles exhibit wave-like properties, and all waves exhibit particle-like properties.
b. Wave characteristics are more apparent when EMR interacts with objects having dimension similar to the photon’s wavelength (Fig. 2-5A).
c. Particle characteristics of EMR, on the other hand, are more evident when an object’s dimensions (e.g., an electron of 10-18 m) are much smaller than the photon’s wavelength (Fig. 2-5B).
 ▪ FIGURE 2-5 Wave- and particle-like properties of light. A. Colors on the CD are produced as light waves that interact with the periodic structure on the tracks on a CD. This is similar to diffraction grating effect, but reflected light diffracts into several beams of different frequencies (color) traveling in different directions. B. Light photons, produced through the interaction of γ-rays with the NaI crystal in a nuclear medicine gamma camera, interact with the photomultiplier tubes and can eject electrons from atoms in the photocathode material in a billiard ball (particle-like fashion). This is known as the photoelectric effect (see Chapter 3). |
2.4 IONIZING AND NONIONIZING RADIATION
1. Ion: an atom or molecule that has lost or gained one or more electrons and has a net electrical charge.
2. Ionizing radiation: photons of higher frequencies in far UV region of spectrum (shorter than 200 nm) with sufficient energy per photon to eject electrons from their atomic shells (e.g., x- and γ-rays).
3. Nonionizing radiation: EMR with photon energies in and below the UV region (e.g., visible, infrared (IR), terahertz (THz), microwave (MW), and radio frequency (RF) waves). Energy transfer occurs as electron excitation and photochemical reactions (IR, optical and UV) and heating due to increased molecular vibration and induced currents (THz, MW and RF).
4. Ionization energy: minimum energy to remove the outermost atomic electron in its ground state (approximately 13.6 eV).
5. Average energy expended per ion pair (W) is larger than the minimum ionization energy due to nonionizing energy losses from excitation and small kinetic energy transfers (approximately 33.7 eV).
2.5 PARTICULATE RADIATION
Particulate radiations import to radiology and nuclear medicine are shown in Table 2-1.
1. Proton: found in nuclei of all atoms, positive electric charge identical to nucleus of H atom
2. Electron: in atomic orbit, charge equal in magnitude but opposite (negative), approximately 1/1,800 mass of proton
3. Beta particles: electrons emitted by the nuclei of radioactive atoms; beta-minus particles (β–) indistinguishable from orbital electrons except for their origin
4. Beta-plus particles (β+) or positrons: positively charged electrons; a form of “antimatter” that ultimately combines with electrons in a unique transformation in which their rest mass (m) is converted through annihilation to an equivalent amount of energy in the form of two oppositely directed 511 keV photons
5. Neutron: uncharged nuclear particle, mass slightly greater than proton; released in nuclear fission and can be used to irradiate stable nuclides in order to produce radioactive nuclides “radionuclides”
6. Alpha particle: a He nucleus with 2 protons and 2 neutrons giving a +2 charge; typically, harmless when external to the body, although can cause extensive cellular damage within the body if the dose is sufficient
TABLE 2-1 PROPERTIES OF PARTICULATE RADIATION | ||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||
2.6 MASS-ENERGY EQUIVALENCE
1. The relationship between the mass and the energy in any system is expressed in one of the most famous equations in science based on Einstein’s ground-breaking work:
where E = energy in joules (J) (where 1 kg m2s-2 = 1 J), m = mass at rest (kg), and c = the speed of light in a vacuum (approximately 2.998 × 108 m/s). The implication is for any mass at rest of m (kg), there is an equivalent of energy E (J) equal to its mass (kg) times the speed of light squared (m2s-2).
2. A notable equivalence of mass and energy: the electron, with m = 9.109 ×10-31 kg, E = 0.511 MeV = 511 keV
3. Atomic mass unit (amu), 1 amu = 1/12 the mass of 12C atom = 931.5 MeV
2.7 STRUCTURE OF THE ATOM
1. The nature of atomic constituents
a. The atom is composed of an extremely dense positively charged nucleus, containing protons and neutrons, and an extranuclear cloud of light, negatively charged electrons
b. Number of protons = number of electrons, so atom is electrically neutral in its normal “typical” state
c. The atom is comprised of largely unoccupied space, in which the volume of the nucleus is only 10-12 (a millionth of a millionth) the volume of the atom
d. Number of electrons in the valence shell of the atom determines its reactivity, or the tendency to form chemical bonds with other atoms
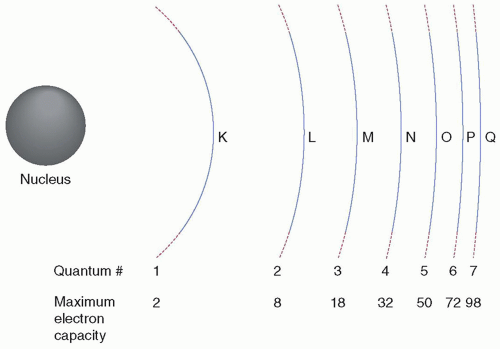
2. Electron orbits
a. The Bohr model: Early model of the electron orbitals
(i) Each electron occupies a discrete energy state in a given electron shell, assigned the letters K, L, M, N, …, with K denoting the innermost shell, in which the electrons have the lowest (i.e., most negative) energy states and the highest binding energy (Fig. 2-6).
(ii) Electrons do not actually revolve in orbits but exist as 3-dimensional waves around the nucleus as a “cloud” of probabilities until something interacts with the cloud and collapses the wavefunction, causing the electron’s position to suddenly appear.
▪ FIGURE 2-6 Electron shell designations and orbital filling rules:
• Shells are assigned the quantum numbers 1, 2, 3, 4, …, with the quantum number 1 designating the K shell.
• Each shell can contain a maximum number of electrons given by 2(n2), where n is the quantum number of the shell.
b. Quantum mechanical model: a 3D wave associated with all matter, including electrons in an atom
(i) The Schrödinger wave equation provides the atomic structure where the location of an orbital electron is described in terms of the probability it will occupy a given location within the atom.
(ii) At any given moment, there is even a probability, albeit extremely low, that an electron can be within the atom’s nucleus; however, the highest probabilities are associated with Bohr’s original atomic radii.
(iii) An electron can have only certain discrete energies inside an atom that agree with the experimental observation of the line spectra in which atoms exhibit and account for the characteristic red and yellow light that neon and sodium bulbs produce.
3. Electron binding energy
a. Orbital energy: energy required to eject (remove) an orbital electron completely from the atom.
(i) For radiation to be ionizing, energy transferred to the electron must equal or exceed its binding energy.
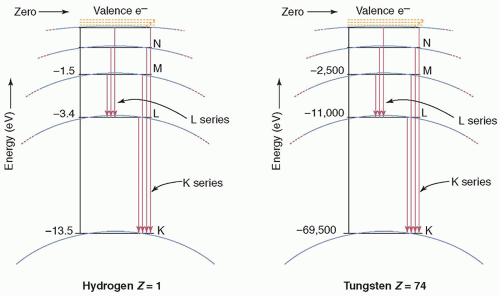
b. Binding energy of inner most shell (K) is greater than outer shells; binding energy also increases with the number of protons in the nucleus (atomic number) (Fig. 2-7).
c. Energy required to move an electron from the innermost electron orbit (K shell) to the next orbit (L shell) is the difference between the binding energies of the two orbits (i.e., EbK – EbL equals the transition energy).
 ▪ FIGURE 2-7 Energy-level diagrams for hydrogen and tungsten. A K shell electron of tungsten with 74 protons in the nucleus is much more tightly bound (approximately 69,500 eV) than the K shell electron of hydrogen orbiting a nucleus with a single proton (approximately 13.6 eV). Note that zero energy represents the point at which the electron is experiencing essentially no coulombic attractive force from the protons in the nucleus (often referred to as a “free” electron). |
2.8 RADIATION FROM ELECTRON TRANSITIONS
Electron cascade: describes the movement of electrons from their normal shell (energy state) to a different shell following the transfer of energy in the form of an x- or γ-ray photon or interaction with a charged particle. The vacancy created is usually filled by an electron transitioning from an outer, more distal shell. Energy of each transition is equal to the difference in binding energy between the original and final shells of the transitioning electron. This energy can be released by the atom as EMR in the form of characteristic x-rays or by transferring the energy to an even more weakly bound electron in the same atom and ejecting it (Auger electron).
Related posts:
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
