Radiation and the Atom
Radiation simply refers to energy that propagates through space or matter. Two categories of radiation of importance in medical imaging are electromagnetic radiation (EMR) and sub-atomic particulate radiation. Several forms of EMR are used in diagnostic imaging.
Diagnostic imaging began with the discovery of x-rays. X-rays are used in the most common medical imaging examinations, including radiography, fluoroscopy, and computed tomography. When electrons are accelerated across a high electrical potential difference in an x-ray tube and strike a target electrode, a small fraction of the electrons (but still a very large number) interact with atomic nuclei in the target, producing a vast quantity of x-rays.
In diagnostic nuclear medicine, radiopharmaceuticals (chemicals or other substances labeled with radioactive materials) are administered to patients. Gamma rays, characteristic x-rays, or pairs of annihilation photons (depending upon the radioactive material) are emitted as a result of unstable nuclei of the radioactive atoms transforming to more stable energy states during the process of radioactive decay (nuclear transformation). The radiation from the patients is detected and the resultant information is used to create images showing the distribution of the radiopharmaceuticals in the patients.
Visible light, another form of EMR, is produced when x-rays, γ-rays, or charged particles interact with scintillators in radiation detectors in x-ray and nuclear medicine imaging devices. Radiofrequency EMR, near the FM frequency band, is used to excite protons and receive signals in magnetic resonance imaging (MRI).
2.1 CLASSICAL ELECTROMAGNETISM
Classical electrostatics is a branch of physics that studies the interactions between stationary electric charges using an extension of the classical Newtonian model. The sources of magnetic fields were identified and studied later as a separate topic. Undoubtedly one of the most profound contributions to science that is on par with those of Newton, Planck, and Einstein were the contributions of James Maxwell. Maxwell took the experimental laws of Coulomb, Gauss, Faraday, and Ampere and unified electricity, magnetism, and optics into a symmetric coherent set of equations. The more than 20 equations developed by Maxwell were reduced to the four more commonly used mathematical expressions of the Laws of Maxwell by British physicist Oliver Heaviside. These four equations, known collectively as Maxwell’s Equations, describe how electric and magnetic fields propagate and interact, and how they are influenced by objects they encounter. Many if not all of the aspects of electromagnetic fields are covered in introductory physics classes and include such topics as Gauss’ law that relates the distribution of electric charge to the resulting electric field; Coulomb’s law that describes the force between two stationary, electrically charged particles; Faraday’s law of electromagnetic induction that describes how an electric current produces a magnetic field and vice versa; and Ampere’s law that relates magnetic field strength to the electric current that produces it. Many of these and other fundamental principles of physics are reviewed in Appendix A. Maxwell’s equations set the stage for the era of modern physics, laying the foundation even for such fields as special relativity
and quantum mechanics. One of the revelations to come out of quantum mechanics was the concept that a particle that is bound (confined spatially) can only take on certain discrete values of energy, called energy levels. This contrasts with classical particle physics, in which a particle or system can have any amount of energy. These energy levels are commonly used to describe how much energy is required to eject electrons from different orbitals in atoms, ions, or molecules, which are bound by the electric field of the nucleus, but can also refer to energy levels of nuclei or vibrational or rotational energy levels in molecules. Einstein introduced the idea that light itself is made of such discrete units of energy, a theory that was later validated empirically. The term photon was given to describe these discrete quantities or “packets” of electromagnetic energy. The energies of photons are commonly expressed in units of electron volts (eV). The evolution of this discovery and its implications continues in Section 2.3. One electron volt is defined as the energy acquired by an electron as it traverses an electrical potential difference (voltage) of one volt in a vacuum. Multiples of eV common to medical imaging are keV (1,000 eV) and MeV (1,000,000 eV).
and quantum mechanics. One of the revelations to come out of quantum mechanics was the concept that a particle that is bound (confined spatially) can only take on certain discrete values of energy, called energy levels. This contrasts with classical particle physics, in which a particle or system can have any amount of energy. These energy levels are commonly used to describe how much energy is required to eject electrons from different orbitals in atoms, ions, or molecules, which are bound by the electric field of the nucleus, but can also refer to energy levels of nuclei or vibrational or rotational energy levels in molecules. Einstein introduced the idea that light itself is made of such discrete units of energy, a theory that was later validated empirically. The term photon was given to describe these discrete quantities or “packets” of electromagnetic energy. The energies of photons are commonly expressed in units of electron volts (eV). The evolution of this discovery and its implications continues in Section 2.3. One electron volt is defined as the energy acquired by an electron as it traverses an electrical potential difference (voltage) of one volt in a vacuum. Multiples of eV common to medical imaging are keV (1,000 eV) and MeV (1,000,000 eV).
2.2 ELECTROMAGNETIC RADIATION
Radio waves, visible light, x-rays, and γ-rays correspond to different frequencies of EMR. Such radiation carries no mass, is largely unaffected at low energies by either electric or magnetic fields, and has a constant speed in each medium. Although EMR propagates through matter, it does not require matter for its propagation. Its maximal speed (2.998 × 108 m/s) occurs in a vacuum. In matter such as air, water, or glass, its speed is reduced by the refractive index of the material. EMR travels in straight lines unless it is altered in direction through interactions with matter, a process referred to as attenuation. Attenuation (the removal of EMR from its straight-line trajectory) can occur (1) by multiple scattering events within atoms or even atomic nuclei, (2) through the absorption (removal of the radiation) by atoms or nuclei, or (3) at energies beyond a million eV, through a transformation of a photon, into particulate matter (e.g., energy to mass conversion of a photon to electron and positron pairs near the field of a nucleus).
Unlike a Newtonian universe, in the context of special relativity, the time-lapse between two events is not invariant from one observer to another but rather is dependent on the relative speeds of the observers. Also, rather than seeing time and the three dimensions of space as separate entities, they are interwoven into a single continuum known as “spacetime.” We can use some of Newton’s ideas to describe many of the physical interactions that occur with radiation in medical imaging. However, it is important to understand that Newton did not realize that we live in a spacetime continuum, nor that E = mc2, and it is these ideas that describe such things as the transformation of mass into energy. The most common example of this in medical imaging occurs shortly after a positive electron (positron) is emitted during each decay of the radioisotope F-18. The rest mass of the positron and that of another electron are converted into the two oppositely directed 511 keV annihilation radiation photons used in positron emission tomography (PET).
More than 100 years have passed since English scientists used a total solar eclipse to prove a revolutionary new theory of gravity—the brainchild of Albert Einstein that would turn this exceptional scientist into a superstar whose name is synonymous with genius. Nobel laureate J.J. Thompson (credited with the discovery of the electron) called general relativity “one of the greatest achievements in human thought.” In Einstein’s general theory of relativity, gravity is treated as a phenomenon resulting from the curvature of the fabric of spacetime. This curvature is caused by and is proportional to the presence of mass. Einstein’s general theory predicted, among other things, that gravitational fields warp the fabric of spacetime causing light to bend as it simply follows the shortest path in the spacetime domain. However, the degree of
bending predicted was so small per unit mass that it would require a truly massive object (like our sun) to be observable. The total solar eclipse in 1919 provided the opportunity for British astronomer Arthur Eddington to ascertain that the light rays from distant stars had been diverted off their paths by the gravitational field of the sun by the amount predicted in Einstein’s theory.
bending predicted was so small per unit mass that it would require a truly massive object (like our sun) to be observable. The total solar eclipse in 1919 provided the opportunity for British astronomer Arthur Eddington to ascertain that the light rays from distant stars had been diverted off their paths by the gravitational field of the sun by the amount predicted in Einstein’s theory.
2.2.1 Electromagnetic Radiation Spectrum
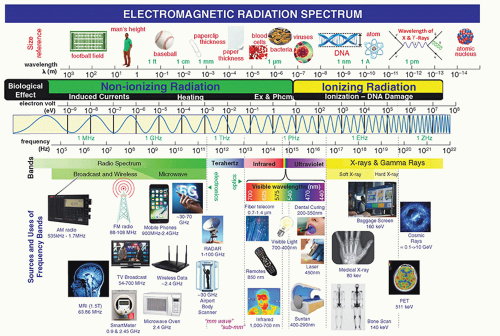
EMR is commonly characterized by its wavelength (λ) and frequency (ν), or energy (E) that equals hν, where h is Planck’s constant (6.62607004 × 10-34 m2 kg/s). Naturally occurring and technologically generated EMR can be produced over a continuous spectrum of a wide range of wavelengths, frequencies, and energies that are collectively referred to as the EM spectrum. For convenient reference, the EM spectrum is divided into categories that include the radio spectrum (involving transmissions from technologies such as AM, FM, and TV broadcasting; cellular and cordless telecommunication systems; as well as other wireless data and power transfer and communications technologies); infrared radiation (i.e., radiant heat); visible light, ultraviolet (UV) radiation; and x- and Gamma (γ) rays (Fig. 2-1).
2.2.2 Wave Characteristics of Electromagnetic Radiation
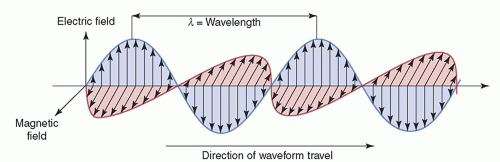
Any wave (EM or mechanical, such as sound) can be characterized by its amplitude (maximal height), wavelength (λ), frequency (ν), and period (τ). The intensity of the wave is proportional to the square of the amplitude. The wavelength is the distance between any two identical points on adjacent cycles. The time required to complete one cycle of a wave is the period. The number of periods that occur per second is the frequency (1/τ). Phase is the temporal shift of one wave relative to another. Some of these quantities are depicted in Figure 2-2. The speed (c), wavelength, and frequency of all EM waves in a vacuum are related by

Because the speed of EMR is constant in a given medium, its frequency and wavelength are inversely proportional to each other. Wavelengths of x-rays and γ-rays are typically measured in fractions of nanometers (nm), where 1 nm = 10-9 m. Frequency is expressed in hertz (Hz), where 1 Hz = 1 cycle/s.
The speed (v) of any wave in a medium with refractive index (n) is described by

EMR propagates as a pair of oscillating and mutually reinforcing electric and magnetic fields that are orthogonal (perpendicular) to one another and to the direction of propagation, as shown in Figure 2-3.
Problem: Find the frequency of blue light with a wavelength of 400 nm in a vacuum. Solution: From Equation 2-1
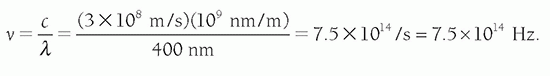
2.2.3 Penetration of Electromagnetic Radiation in Tissue
To interrogate the physical or chemical structure of organs and tissues within the body through imaging with EMR, the energy of the EMR must be able to penetrate and interact with the organ and tissue of interest. The interactions must produce signals that
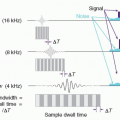
in a way that can help differentiate between normal tissue and the presence of disease. As seen in Figure 2-4, after traversing 25 cm of soft tissue, a beam of EMR (the interrogating signal) in the low frequency or low energy portion of the spectrum is rapidly attenuated, transmitting only 1% of the incident beam at 300 MHz (1 m). However, at lower frequencies in the TV and FM broadcast portion of the spectrum (including the ˜64 MHz signals received from hydrogen nuclei in a 1.5 Tesla [T] MRI), much less attenuation takes place. At the higher frequency or photon energy portions of the EMR spectrum, where x- and γ-rays are used in medical imaging, the opposite relationship holds between frequency, photon energy, and attenuation, because as the frequencies and photon energies increase, the fraction of the incident radiation transmitted increases. Nevertheless, as will be discussed in several upcoming chapters, as the photon energy of the EMR increases, there is a trade-off between the ability of the radiation to penetrate the anatomy of interest, the detection efficiency of the image receptor, and the amount of “noise,” or decrease in available contrast observed in the final image.
in a way that can help differentiate between normal tissue and the presence of disease. As seen in Figure 2-4, after traversing 25 cm of soft tissue, a beam of EMR (the interrogating signal) in the low frequency or low energy portion of the spectrum is rapidly attenuated, transmitting only 1% of the incident beam at 300 MHz (1 m). However, at lower frequencies in the TV and FM broadcast portion of the spectrum (including the ˜64 MHz signals received from hydrogen nuclei in a 1.5 Tesla [T] MRI), much less attenuation takes place. At the higher frequency or photon energy portions of the EMR spectrum, where x- and γ-rays are used in medical imaging, the opposite relationship holds between frequency, photon energy, and attenuation, because as the frequencies and photon energies increase, the fraction of the incident radiation transmitted increases. Nevertheless, as will be discussed in several upcoming chapters, as the photon energy of the EMR increases, there is a trade-off between the ability of the radiation to penetrate the anatomy of interest, the detection efficiency of the image receptor, and the amount of “noise,” or decrease in available contrast observed in the final image.
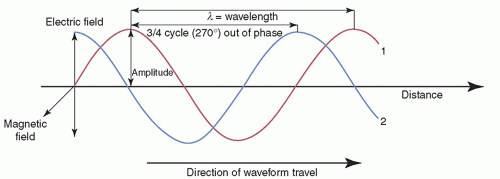 ▪ FIGURE 2-2 Characterization of EM waves, of equal wavelength and amplitude, but with wave #2 having a 3/4 cycle phase difference. The magnetic field component is not shown for clarity (see Fig. 2-3). |
2.3 BEHAVIOR OF ENERGY AT THE ATOMIC SCALE: ONE OF THE MOST IMPORTANT DISCOVERIES IN THE HISTORY OF SCIENCE
At the turn of the 19th century, physicists were trying to define the mathematical relationship between the color of light emitted by some objects as they were heated (i.e., color spectrum) and the object’s temperature. Using classical mechanics and
electromagnetism, they envisioned that, at equilibrium, energy is shared evenly amongst all the accessible modes of motion (e.g., translation, rotation, vibration). This led to them to conclude that a continuous relationship existed between the energy of the modes of motion (degrees of freedom), such as the frequencies of vibrations, and the colors of the emitted light. At low temperatures, the vibrations were slower and therefore emitted more red light, but at higher temperatures, the vibrations were faster and emitted more blue light. Lord Rayleigh and Sir James Jeans developed an equation (Rayleigh-Jeans law) that implied that the radiated power per unit frequency should be proportional to the square of the frequency. While this law accurately predicted experimental results at low frequency, the intensity of EMR predicted at higher frequencies of the EM spectrum was far greater than observed. Worse yet, the intensity of EMR appeared to approach infinity as frequency increased! The failure of Rayleigh-Jeans law to accommodate this discrepancy showed that there was something wrong with the law, with classical electromagnetic theory, or with both. The problem was that in classical physics everything (mass, energy, speed, time, etc.) was observed to be continuous and could be added or divided into infinitesimally smaller quantities.
electromagnetism, they envisioned that, at equilibrium, energy is shared evenly amongst all the accessible modes of motion (e.g., translation, rotation, vibration). This led to them to conclude that a continuous relationship existed between the energy of the modes of motion (degrees of freedom), such as the frequencies of vibrations, and the colors of the emitted light. At low temperatures, the vibrations were slower and therefore emitted more red light, but at higher temperatures, the vibrations were faster and emitted more blue light. Lord Rayleigh and Sir James Jeans developed an equation (Rayleigh-Jeans law) that implied that the radiated power per unit frequency should be proportional to the square of the frequency. While this law accurately predicted experimental results at low frequency, the intensity of EMR predicted at higher frequencies of the EM spectrum was far greater than observed. Worse yet, the intensity of EMR appeared to approach infinity as frequency increased! The failure of Rayleigh-Jeans law to accommodate this discrepancy showed that there was something wrong with the law, with classical electromagnetic theory, or with both. The problem was that in classical physics everything (mass, energy, speed, time, etc.) was observed to be continuous and could be added or divided into infinitesimally smaller quantities.
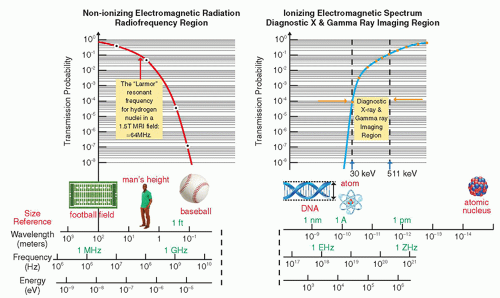 ▪ FIGURE 2-4 Attenuation of electromagnetic energy in the radiofrequency and diagnostic x- and γ-ray regions of the electromagnetic spectrum as it is transmitted through 25 cm of soft tissue. The Larmor (or precessional) frequency of the hydrogen nuclei in a 1.5 tesla (T) magnetic resonance imaging (MRI) system is ˜64 MHz that provides a measurable signal to generate images of soft tissue as discussed in Chapter 12. Diagnostic x-ray and γ-ray energies between ˜30 keV and 511 keV have sufficient transmission probability to generate images as discussed in Chapters 7, 8, 9, 10, 18 and 19. |
2.3.1 Energy Quanta and the Photon
During that same time, German physicist Max Planck was also examining the nature of light and thermodynamics, and struggled with the possibility of having an infinite number of vibrational states at low energy. Planck observed that matter absorbed or emitted energy only in restricted amounts. In 1900, out of frustration, desperation, and no doubt partly ingenuity, he proposed a radical concept, that particles could only vibrate, be emitted or absorbed at energies that corresponded to multiples of some minimal finite discrete packets of energy he called quanta. This minimum
energy was defined by the product of the frequency of vibration and a constant, h, as Emin = hv. Today, these discrete finite (i.e., particle-like) packets of EM energy are called photons. The energy of a photon is given by
energy was defined by the product of the frequency of vibration and a constant, h, as Emin = hv. Today, these discrete finite (i.e., particle-like) packets of EM energy are called photons. The energy of a photon is given by

where Planck’s constant (h) = 6.626 × 10-34 J-s = 4.136 × 10-18 keV-s. When E is expressed in keV and λ in nanometers (nm),

This incredibly small constant h of 6.62618 × 10-34 J-s was not only consistent with the experimental data at all frequencies of EMR but it also had the effect of limiting the amount of energy the high-frequency vibrations could hold. This was an astonishing discovery because it challenged the idea that all forms of energy were continuous and could be transferred in any amounts. While the inventor of what would be known as the quantum hypothesis did not realize it at the time, Planck’s discovery would open up a completely new field of research in physics called quantum mechanics, responsible for a great diversity of new technologies (e.g., cell phone, personal computer, DVD, and MRI) that make modern life and healthcare possible—and even reduces to classical physics in the appropriate regime.
2.3.2 Particle Characteristics of Electromagnetic Radiation
Prior to the advent of quantum mechanics, the classical wave description of EMR could not accommodate the observation that, upon absorbing EMR, the kinetic energies of electrons ejected from an atom (referred to as photoelectrons) depended on the energy (or wavelength) of the incident radiation, rather than the intensity or number of incident photons per unit area (i.e., fluence). In 1905, Albert Einstein resolved this issue by postulating that Planck’s quanta were acting like physical particles—namely photons. For this bold elucidation, of what is now known as the photoelectric effect, Albert Einstein received the Nobel Prize in Physics in 1921.
2.3.3 Wave-Particle Duality
As previously discussed, there are two equally correct ways of describing EM radiation—as waves and as photons—the discrete particle-like packets or quanta of energy. A central tenet of quantum mechanics is that all particles exhibit wave-like properties and all waves exhibit particle-like properties. This “wave-particle duality,” initially proposed in 1924 by future Nobel Laureate Louis de Broglie, addresses the inadequacy of classical Newtonian mechanics in fully describing the behavior of atomic and sub-atomic objects. Wave characteristics are more apparent when EMR interacts with objects having dimensions similar to the photon’s wavelength. For example, light photons with wavelengths of ˜4-7 × 10-7 m are separated into colors by a diffraction grating of tracks on a compact disc (CD) where the track separation (1.6 × 10-6 m) is of the same order of magnitude as the wavelength of light, as shown in Figure 2-5A. Particle characteristics of EMR, on the other hand, are more evident when an object’s dimensions (e.g., an electron of 10-18 m) are much smaller than the photon’s wavelength. For example, light photons, produced through the interaction of γ-rays with the NaI crystal in a nuclear medicine gamma camera, interact with the
photomultiplier tubes (PMTs, Fig. 2-5B) and can eject electrons from atoms in the photocathode material. The PMTs, which are optically coupled to the crystal, direct the ejected electrons via a focusing electrode toward a series of dynodes where electrons are multiplied thus providing an amplified electrical signal for the formation of an image (discussed in Chapter 18).
photomultiplier tubes (PMTs, Fig. 2-5B) and can eject electrons from atoms in the photocathode material. The PMTs, which are optically coupled to the crystal, direct the ejected electrons via a focusing electrode toward a series of dynodes where electrons are multiplied thus providing an amplified electrical signal for the formation of an image (discussed in Chapter 18).
 ▪ FIGURE 2-5 Wave- and particle-like properties of light. A. A CD is pressed with tracks (either with bit pits, or just a groove for photosensitive dye), followed by a aluminized covering layer. Colors on the CD are produced as light waves interact with the periodic structure of the tracks on a CD. The effect seen on the CD is similar to a diffraction grating effect, but in this case the reflected light diffracts into several beams of different frequencies (color) traveling in different directions. B. The imaging chain in nuclear medicine begins when γ-rays interact with the NaI crystal of a gamma camera (not shown) producing light. The NaI crystal is optically coupled to the surface of a number of PMTs like the one shown above. Just below the glass surface of the PMT, light photons strike the photocathode, ejecting electrons in a classical billiard ball (particle-like) fashion. This process is the photoelectric effect described by Einstein for which he was awarded the Nobel Prize in Physics in 1921. Additional details regarding the photoelectric effect as it applies to higher energy EMR (x-ray and γ-rays) is provided in Chapter 3. The ejected electrons are subsequently accelerated and amplified in the PMT, thereby increasing the gain of the signals used to localize the γ-ray interactions. Nuclear medicine imaging systems are discussed in Chapters 18 and 19. |
The particle-like behavior of x-rays is also exemplified by the classical “billiardball” type of collision between an x-ray photon and an orbital electron in Compton scattering. Similarly, the x-ray photon’s energy is completely absorbed and results in the ejection of a tightly bound inner shell electron (a photoelectron) in the photoelectric effect. Each of these interactions is important in medical imaging and will be discussed further in Chapter 3.
2.4 IONIZING AND NON-IONIZING RADIATION
An atom or molecule that has lost or gained one or more electrons and has a net electrical charge and is called an ion (e.g., sodium ion or Na+). Some but not all electromagnetic and particulate radiations can cause ionization. In general, photons of higher frequency than the far UV region of the spectrum (i.e., wavelengths shorter than 200 nm) have sufficient energy per photon to remove bound electrons from atomic shells, thereby producing ionized atoms and molecules. Radiation in this portion of the spectrum (e.g., x-rays and γ-rays) is called ionizing radiation. EMR with photon energies in and below the UV region (e.g., visible, infrared, terahertz, microwave, and radio waves) is called non-ionizing radiation.
The threshold energy for ionization depends on the type and state of matter. The minimum energies required to remove the outermost electron of an atom in
its ground state is referred to as the ionization energy. For calcium (Ca), glucose (C6H12O6), and liquid water (H2O), these thresholds are 6.1, 8.8, and 11.2 eV, respectively. As water is the most abundant (thus most likely) molecular target for radiation to interact within the body, a practical radiobiological demarcation between ionizing and nonionizing EMR is approximately 11 eV. While 11 eV is the lowest photon energy able to ionize water, in a random set of ionization events in a medium, the average energy expended per ion pair (W) is larger than the minimum ionization energy due to non-ionizing energy losses from excitation and small kinetic energy transfers. For water and tissue-equivalent gas, W is about 30 eV. Particles such as high-speed electrons, protons, and α particles (discussed below) can also produce ionization. Energetic charged particles and EM radiation interactions are discussed further in Chapter 3.
its ground state is referred to as the ionization energy. For calcium (Ca), glucose (C6H12O6), and liquid water (H2O), these thresholds are 6.1, 8.8, and 11.2 eV, respectively. As water is the most abundant (thus most likely) molecular target for radiation to interact within the body, a practical radiobiological demarcation between ionizing and nonionizing EMR is approximately 11 eV. While 11 eV is the lowest photon energy able to ionize water, in a random set of ionization events in a medium, the average energy expended per ion pair (W) is larger than the minimum ionization energy due to non-ionizing energy losses from excitation and small kinetic energy transfers. For water and tissue-equivalent gas, W is about 30 eV. Particles such as high-speed electrons, protons, and α particles (discussed below) can also produce ionization. Energetic charged particles and EM radiation interactions are discussed further in Chapter 3.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree