Chapter 2 Radiation interactions with matter
Introduction
Excitation and ionization
Ionizing radiation, by definition, has sufficient energy to ionize matter. That is, it has sufficient energy to overcome the binding energy of atomic electrons. Radiation of energy below the binding energy of a particular electron shell may still interact with an electron by raising it to a higher, vacant shell (see Chapter 1). As a result of this interaction, the atom has gained energy and is left in an excited state (Figure 2.1A). It will eventually lose this excess energy to return to its lowest energy state, or ground state. An electron occupying an outer shell relative to the vacancy may achieve a lower energy state by filling the vacancy (Figure 2.1C). The excess energy is released as a characteristic photon (of energy equal to the difference in shell binding energies). If this electron is also in an inner shell, it too will leave behind a vacancy which an outer electron can again occupy (Figure 2.1C) losing energy in the form of a characteristic photon. This process results in a cascade of electrons moving between shells and a corresponding set of characteristic photons which eventually returns the atom to its ground state.
Even if its own kinetic energy exceeds the atomic electron’s binding energy, an incoming particle (electron, photon etc.) may transfer just part of its kinetic energy to an atomic electron to produce excitation. Where the incoming particle transfers more than the binding energy of an atomic electron to the atom, the electron in question is ejected from the atom, with kinetic energy equal to the total energy transferred, minus the binding energy. As a result of losing an electron, the atom has been ionized (Figure 2.1B). As well as being chemically reactive as a result of this interaction (the positive ion will seek an electron from its surroundings to return to its uncharged state), any electron ejected from an inner shell will leave a vacancy behind, which represents an excited state. A cascade process will then follow as described above as de-excitation takes place (Figure 2.1D).
Electron interactions
Range and path-length
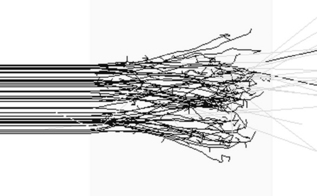
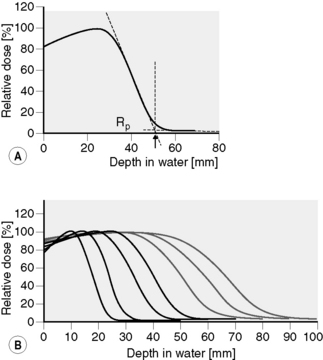
Electrons have a negative charge and a relatively small mass. As a result, electron transport through matter is characterized by a large number of interactions through which generally a small amount of energy is lost in each event and a high degree of scattering occurs (Figure 2.2). Because of these frequent interactions, it can often be assumed that electrons lose energy continuously as they traverse matter and to a good approximation the energy loss can be assumed to be at a constant rate. It follows that if electrons (or any other particles) lose energy continuously, then they must have a finite range. This is true of all charged particles. Calculated ranges for charged particles can be performed using this continuous slowing down approximation, resulting in the csda range. If a beam of monoenergetic electrons is incident on a given material and we assume continuous energy loss, then the total distance travelled, or path length, must be the same for all electrons in the beam. The depth of penetration, or range, will vary due to the different paths traversed by individual electrons as indicated in Figure 2.2. This range-straggling leads to a slope in the measured depth-dose curve as illustrated in Figure 2.3A. The steepness of this slope decreases as electron energy is increased, as shown in Figure 2.3B. Note that the dose does not fall to zero immediately beyond the steep region of dose fall-off, due to bremsstrahlung photons being produced (discussed in the next section). The intersection between the slope due to range-straggling and the bremsstrahlung tail, gives the practical range of the electron beam, Rp. As a guide, for clinical electron beams produced by linear accelerators (approximately 4–20 MeV), the range of electrons in water (or tissue) can be approximated by:
An indication of the accuracy of the above expression can be made by comparison with electron csda ranges in water, given in Table 2.1.
Table 2.1 Electron csda (continuous slowing down approximation) ranges in water
| Electron beam energy (MeV) | csda range (cm) |
|---|---|
| 0.1 | 0.01 |
| 0.25 | 0.06 |
| 0.5 | 0.18 |
| 1 | 0.44 |
| 5 | 2.55 |
| 10 | 4.98 |
| 25 | 11.3 |
| 50 | 19.8 |
Evaluated using the ESTAR program [1]
Collisional and radiative (bremsstrahlung) energy loss
The last section was concerned with the dominant interaction that a beam of electrons undergoes when traveling through matter, that of collisions with atomic electrons (in the energy range of interest to radiotherapy, at least). These interactions lead to excitation and ionization of the medium traversed, as represented schematically in Figure 2.2. More rarely, electrons from an incident clinical beam will pass near to and interact with the atomic nucleus, again as a result of the Coulomb force of attraction between negatively charged electron and positively charged nucleus. The path (and momentum) of the incident electron is changed under the influence of the nucleus, resulting in a loss of electron energy. This loss of energy appears as a radiated photon, or x-ray photon (radiative energy loss). The term, bremsstrahlung (‘braking radiation’), is a helpful descriptive name given to this process, shown schematically in Figure 2.4. The probability of this interaction occurring is inversely proportional to the square of the incident particle’s mass. As a result, bremsstrahlung is only significant for electrons. This important process by which x-ray photons can be produced is described further below.
Stopping power and linear energy transfer (LET)
If energy is in MeV and distance in centimetres, stopping power has units of MeV cm−1. Alternatively, we may express this in terms of mass stopping power, S(E)/ρ, where ρ is the material density (g cm−3). The magnitude of this quantity depends on both the energy of the electron and the material involved. Figure 2.5 shows the variation of electron mass stopping power with energy in water and lead. As stopping power reflects the difference in energy absorption between materials, it is used in radiation dosimetry to convert measured radiation dose between materials. For example, using an air-filled ionization chamber surrounded by water, a direct measurement of energy absorbed, or dose to air, Dair, can be made. The dose, Dw, that would be absorbed if the ionization chamber were replaced by water (or a patient) would be given by multiplying by the ratio of mass stopping powers between water and air:
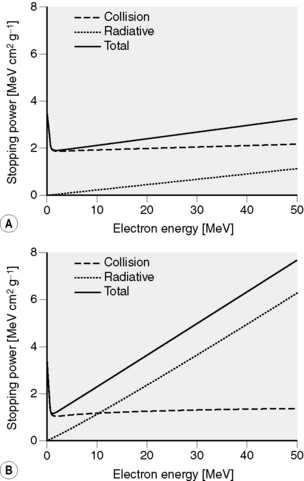
Figure 2.5 Collisional, radiative and total stopping power for electrons. (A) in water and (B) in tungsten. Data calculated using ESTAR [1].
where ρw and ρair are the densities of water and air, respectively. Strictly, the stopping power used in the above expression must be restricted to energy absorbed within the ionization chamber volume and must exclude any energy that is lost from the beam but travels beyond the chamber (site of interaction). For example, energy lost in the form of bremsstrahlung, or collisions in which a large amount of the incident electron’s energy is transferred to an atomic electron such that it travels beyond the chamber.
Linear energy transfer (LET) also refers to the amount of energy deposited by ionizing radiation in matter. Units are also energy per unit length, often expressed in keV μm−1. LET is commonly used to distinguish between ionizing radiation in relation to radiobiology; radiation having a higher LET (such as protons, alpha particles) will generally lead to a greater biological effect than low LET radiation (photons, electrons). The smaller length units (μm) for LET reflect its application to energy deposition over subcellular dimensions. A schematic comparison between energy deposition for high and low LET beams is illustrated in Figure 2.6.
X-ray production
The energy of the electron beam is dictated by the maximum photon energy required. The use of high atomic number materials, gives the best yield of photons. Table 2.2 indicates the proportion of electron beam kinetic energy converted to photons for a tungsten target. The remainder of the incident electron’s kinetic energy is lost through collisions with atomic electrons in the target, causing excitation and ionization. A large amount of this energy is eventually released in the form of heat, requiring the target to be cooled.
Table 2.2 Percentage of incident electron beam energy appearing as bremsstrahlung for electrons incident on a tungsten target
| Electron Energy (MeV) | Photon Yield (%) |
|---|---|
| 0.05 | 0.5 |
| 0.25 | 2 |
| 1 | 6 |
| 10 | 30 |
| 50 | 63 |
Data calculated using ESTAR [1]
In the bremsstrahlung process, an electron may lose any amount of energy, up to its total kinetic energy. Rather than discrete photon energies, as are observed during de-excitation of atoms, a continuous spectrum of photon energies is produced. An example of the photon spectra produced when electrons are used to generate a 100 kV and 6 MV photon beam is shown in Figure 2.7. Photon spectra are commonly designated by ‘kV’ or ‘MV’ to indicate the nominal potential used to accelerate the electrons that created the spectrum. For example, a potential difference of 100 kV between cathode and anode in an x-ray tube will result in 100 keV electrons striking the target, producing a 100 kV photon spectrum. While there is no lower limit on the energy of photons produced, the low energy components of the spectrum are preferentially removed by photon attenuation within the target and other machine components, so that the peak in the spectrum occurs at approximately one-third of the maximum photon energy. Discrete spectral lines can be seen superimposed on the continuous 100 kV spectrum, these are due to characteristic photons being produced during de-excitation of tungsten atoms after inner shell electrons have been excited or ejected through collisions with the incident electron beam. The energies of these characteristic photons correspond to the difference between the binding energies of the inner shell vacancy and the outer shell electron that fills the vacancy. The difference between electron binding energies depends on the atomic number of the target. For tungsten, with a K-shell binding energy of 69 keV and L-shell binding energy of 12 keV, it follows that the minimum energy of a characteristic photon produced by filling an electron vacancy in the K-shell is 57 keV. The same characteristic photons are not observed in the 6 MV spectrum, as they now represent very low energies within this spectrum and are preferentially removed by photon attenuation.
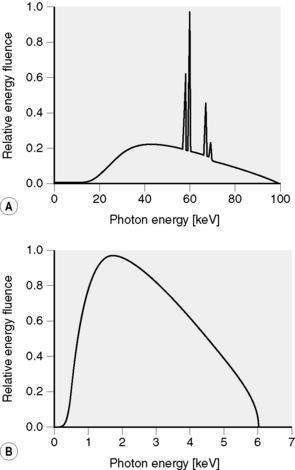
Figure 2.7 X-ray spectra: (A) 100 kV diagnostic spectrum; bremsstrahlung (continuous) spectrum with superimposed discrete characteristic tungsten x-rays [6] and (B) 6 MV photon spectra from an Elekta SL25 linear accelerator [5].
For electrons striking a thin target, photons are produced in all directions. The intensity (or number) in a particular direction depends on the energy of the incident electrons, and the atomic number of the target. For low electron energies (up to 100 keV), the intensity is almost equal in all directions and as the electron energy increases, the photons produced become more forward directed. This variation in photon intensity with incident electron energy is illustrated in Figure 2.8
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree



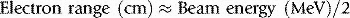 2.1
2.1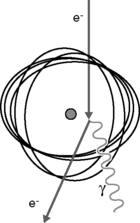
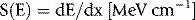 2.2
2.2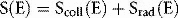 2.3
2.3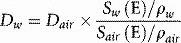 2.4
2.4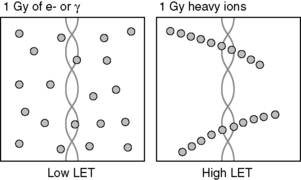
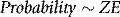 2.5
2.5