Fig. 1
Object extraction methods using contour/surface energy functionals. Only a few representative references are shown for each method
Note that graph cut methods for object extraction, e.g. [4, 8, 9, 39], were preceded by a number of graph-based methods for image “clustering” that use either combinatorial optimization algorithms [22, 32, 63, 67] or spectral analysis techniques, e.g. normalized cuts [60]. Typically, the goal of these methods is to automatically divide an image into a number of “blobs” or “clusters” using only generic cues of coherence or affinity between pixels.1 We focus on a fairly different group of image segmentation methods shown in Fig. 1 that integrate model-specific visual cues and contextual information to accurately delineate particular object of interest.
1.1 Implicit representation of contours/surfaces
To solve an image segmentation problem, one should first decide how to numerically represent contours or surfaces. Many existing segmentation methods (Fig. 1) use explicit representation of contours/surfaces based on meshes or splines defined by a set of moving or “active” control points forming a chain [1, 18, 25, 30, 36]. A 2D contour can be explicitly represented by a set of adjacent edges connecting nodes on a graph [21, 33, 50]. Both contours in 2D and surfaces in 3D can be explicitly represented by a set of adjacent facets on a complex [37].
Many recent segmentation methods use implicit surface representation, see Fig. 1. Implicit object representation is frequently referred to as region-based representation. Such methods store a mask describing object’s interior. Such a mask is a 2D (or 3D) array over pixels (or voxels) assigning different values to interior and exterior regions. For example, standard level-sets methods, e.g. [52, 58], maintain a real valued mask with negative values for interior pixels and positive values for exterior pixels (or vice versa). The object’s boundary is implicit, it is a zero-level set of this real-valued mask. Many level-sets techniques use a mask that closely approximates a signed distance map of the object’s boundary. Real-value precision of the mask also helps to reconstruct the boundary with sub-pixel accuracy, if needed.
Some other implicit techniques, e.g. [2, 15, 16, 27], use a regional mask storing real-values in some bounded interval, e.g. [0, 1]. While each method may provide a different interpretation for mask values, a surface is typically extracted as a 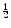 -level set of the mask. If necessary, sub-pixel accuracy can be obtained using bilinear interpolation. Notably, [2] and [16] prove that (in a theoretical case of continuous-resolution) their masks should converge to binary (1/0) values. In particular, this shows that specific choice of a threshold is not essential in [2, 16].
-level set of the mask. If necessary, sub-pixel accuracy can be obtained using bilinear interpolation. Notably, [2] and [16] prove that (in a theoretical case of continuous-resolution) their masks should converge to binary (1/0) values. In particular, this shows that specific choice of a threshold is not essential in [2, 16].
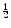 -level set of the mask. If necessary, sub-pixel accuracy can be obtained using bilinear interpolation. Notably, [2] and [16] prove that (in a theoretical case of continuous-resolution) their masks should converge to binary (1/0) values. In particular, this shows that specific choice of a threshold is not essential in [2, 16].
-level set of the mask. If necessary, sub-pixel accuracy can be obtained using bilinear interpolation. Notably, [2] and [16] prove that (in a theoretical case of continuous-resolution) their masks should converge to binary (1/0) values. In particular, this shows that specific choice of a threshold is not essential in [2, 16].Graph cut [4, 8, 9, 39] is another implicit approach to representing object boundaries. Graph cut methods compute a binary-valued mask assigning 1 to interior and 0 to exterior pixels. In this case, object boundary cannot be uniquely identified with sub-pixel accuracy since any curve/surface in a narrow space between 1-0 valued points in 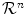 (pixels/voxels) is consistent with the corresponding binary mask. If necessary, one simple way to output a boundary explicitly is to draw a surface following pixels borders. This may work sufficiently well if pixels/voxels are small enough.2 However, even tiny “pixalization” of the surface causes visually noticeable shading artifacts in applications using 3D surface rendering. Thus, fitting a smooth surface in a narrow band between 1 and 0 labeled points in
(pixels/voxels) is consistent with the corresponding binary mask. If necessary, one simple way to output a boundary explicitly is to draw a surface following pixels borders. This may work sufficiently well if pixels/voxels are small enough.2 However, even tiny “pixalization” of the surface causes visually noticeable shading artifacts in applications using 3D surface rendering. Thus, fitting a smooth surface in a narrow band between 1 and 0 labeled points in 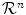 could be a better solution in case of 3D rendering, e.g. [46, 66].
could be a better solution in case of 3D rendering, e.g. [46, 66].
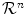 (pixels/voxels) is consistent with the corresponding binary mask. If necessary, one simple way to output a boundary explicitly is to draw a surface following pixels borders. This may work sufficiently well if pixels/voxels are small enough.2 However, even tiny “pixalization” of the surface causes visually noticeable shading artifacts in applications using 3D surface rendering. Thus, fitting a smooth surface in a narrow band between 1 and 0 labeled points in
(pixels/voxels) is consistent with the corresponding binary mask. If necessary, one simple way to output a boundary explicitly is to draw a surface following pixels borders. This may work sufficiently well if pixels/voxels are small enough.2 However, even tiny “pixalization” of the surface causes visually noticeable shading artifacts in applications using 3D surface rendering. Thus, fitting a smooth surface in a narrow band between 1 and 0 labeled points in 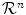 could be a better solution in case of 3D rendering, e.g. [46, 66].
could be a better solution in case of 3D rendering, e.g. [46, 66].1.2 Local vs. Global optimization
Each surface representation approach may have some advantages and disadvantages. For example, methods using control points may suffer from mesh irregularities and from rigid topological structure of surfaces they represent. Discrete approaches based on graphs/trees and dynamic programming must address potential geometric metrication artifacts. Some types of representation are specific to contours in 2D (see Fig. 1) and do not generalize to surfaces in 3D. Moreover, each surface representation approach is typically tied with certain types of energy functionals and optimization algorithms.
The underlying optimization technique significantly affects numerical robustness, convergence, speed, and memory efficiency of the segmentation method. Moreover, it also determines quality guarantees for the solution. For example, some algorithms can find only a local minima near some provided initial guess, while others can compute a globally optimal solution in the whole domain of interest (e.g. image or volume).
The majority of existing techniques with explicit representation of surfaces via control points (meshes, splines) use either variational methods [18, 30, 36] or dynamic programming [1] to find a local optima positions for these control points near some initial guess. Dynamic programming can also be used for global minimization in some 2D segmentation problems. For example, segmentation methods using explicit representation of contours as “edge-paths” on graphs use variations of dynamic programming (e.g. Dijkstra/Viterbi algorithms, ratio cycles, ratio cuts) to obtain globally optimal solutions in 2D applications [21, 33, 50, 65]. Unfortunately, there are no straightforward generalizations of DP-based methods to surfaces in 3D. However, a dual approach explicitly representing contours/surfaces as a set of adjacent facets on complexes allows global optimization via combinatorial graph cut algorithms in either 2D or 3D cases [37].
Many segmentation methods using implicit representation of surfaces via level sets [14, 17, 52] obtain only local minima solutions since they apply gradient descent to non-convex spaces (e.g. of characteristic set functions). More recently, continuous max-flow/min-cut ideas developed by Strang [61] in the early eighties inspired convex relaxation techniques computing globally optimal surfaces [2, 16] using implicit surface representations.
Graph cuts methods for object segmentation [8, 9, 4, 39] represent object boundaries implicitly via binary pixel labeling. Globally optimal labeling is produced by combinatorial algorithms for discrete max-flow/min-cut problems on graphs known since the early sixties [23]. Interestingly, continuous versions of max-flow/min-cut problems formulated by Strang [61] were inspired by the corresponding discrete problems.
First application of combinatorial graph cut algorithms to image analysis dates back to the late eighties [28] (binary image restoration). But graph cuts have become popular in vision only 10 years later when high-quality globally optimal solutions made breakthroughs in stereo [13, 31, 44, 56] and multi-view reconstruction [45, 64, 47]. Before combinatorial graph cut approach to object extraction was first presented in [8], globally optimal object segmentation was possible only in 2D using dynamic programming.
Global optimization and numerically stable fast algorithms (e.g. [10]) are the key strengths of the graph cut framework. In general, global solutions are attractive due to potentially better robustness and predictability. For example, imperfections in a globally optimal solution directly relate to the cost functional rather than to numerical problems during minimization or bad initialization. Yet, global minima could be unacceptable. For example, the trivial null solution is a global minima in some segmentation problems since length/area of the segmentation boundary is a typical regularizing component in most energy functionals. Some methods add a ballooning term to their energy or constrain solution space to avoid trivial/null solutions. Computing local minima could be another reasonable and efficient alternative if good initial solution is available. Interestingly, graph cut approach can also be used for local optimization when the search space is appropriately constrained near given initial solution [11].
1.3 Continuous vs. Discrete Optimization
Energy-based object segmentation methods can be also distinguished by the type of energy functional they use. The majority of methods optimizing segmentation boundary cost can be divided into two groups:
(A)
Optimization of a functional defined on continuous contour/surface
(B)
Optimization of an energy defined on a finite set of discrete variables
The standard methods in group (A) normally formulate segmentation as an optimization problem in an infinite-dimensional space 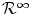 (of continuous contours or functions). Most methods in this group rely on a variational approach and gradient descent. In contrast, segmentation methods from group (B) formulate some integer optimization problem in finite dimensional space
(of continuous contours or functions). Most methods in this group rely on a variational approach and gradient descent. In contrast, segmentation methods from group (B) formulate some integer optimization problem in finite dimensional space 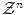 and use combinatorial optimization algorithms. Note that discrete energy functionals in group (B) are frequently designed to approximate some continuous optimization problem. Figure 1 contains examples of methods from both groups (A) and (B).
and use combinatorial optimization algorithms. Note that discrete energy functionals in group (B) are frequently designed to approximate some continuous optimization problem. Figure 1 contains examples of methods from both groups (A) and (B).
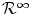 (of continuous contours or functions). Most methods in this group rely on a variational approach and gradient descent. In contrast, segmentation methods from group (B) formulate some integer optimization problem in finite dimensional space
(of continuous contours or functions). Most methods in this group rely on a variational approach and gradient descent. In contrast, segmentation methods from group (B) formulate some integer optimization problem in finite dimensional space 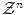 and use combinatorial optimization algorithms. Note that discrete energy functionals in group (B) are frequently designed to approximate some continuous optimization problem. Figure 1 contains examples of methods from both groups (A) and (B).
and use combinatorial optimization algorithms. Note that discrete energy functionals in group (B) are frequently designed to approximate some continuous optimization problem. Figure 1 contains examples of methods from both groups (A) and (B).The methods in group (A) include snakes [36, 18], region competition [69], geodesic active contours [14], other methods based on level-sets [52, 59], and more recent global optimization methods using convex relaxation [2, 16].
Optimization methods in group (B) minimize an energy defined over a finite set of integer-valued variables. Such variables are usually associated with graph nodes corresponding to image pixels, super pixels, cells, or control points. Many methods in group (B) use discrete variables representing “direction” of a path along some graph relying on various versions of dynamic programming to compute optimal paths or cycles [1, 21, 33, 50, 65]. Graph cut methods also belong to group (B). Both implicit [4, 8, 9, 39] and explicit [37] techniques use binary variables representing (object/background) labels for either pixels, voxels, or complex cells. Numerically, graph cut methods rely on combinatorial max-flow/min-cut algorithms [10, 23, 26]. Once appropriate (submodular) discrete energy is formulated [6, 29, 53], these algorithms compute an exact global minima.
Continuous methods in (A) inherently rely on approximating numerical schemes (e.g. finite differences or finite elements) that must be carefully designed to insure robustness and stability. Convergence of such numerical methods is an important and non-trivial issue that has to be addressed. Segmentation results generated by two variational techniques using the same energy may depend on their implementation details.
Discrete optimization methods in (B) are numerically robust and “repeatable”. For example, assuming the same energy function, one would always get identical segments even though one can choose from a number of different combinatorial min-cut/max-flow algorithms for computing minimum s-t cuts on graphs [10, 23, 26].
[10, 20, 35] studied practical efficiency of combinatorial min-cut/max-flow algorithms on applications in computer vision. It was shown that some max-flow techniques could solve 2D and 3D segmentation problems in close to real-time using regular PCs. Graph cut methods allow a user to change hard and soft constraints on-a-fly [4, 7, 8] enabling fast interactive editing of the segments. Significant speed-ups were demonstrated for dynamic segmentation problems using flow-recycling [39] and cut-recycling [34]. While straightforward implementation of graph cuts may require a lot of memory in 3D applications, [46, 49] showed that multi-level and adaptive banded techniques can alleviate the problem. Recent region-push-relabel algorithm [20]3 demonstrated good scalability to large 3D volumes under limited memory resources and significant speed-ups for multi-processor PCs.
1.4 Integrating Boundary and Regions
Continuous surface functionals in group (A) can incorporate various regional and boundary properties of segments motivated by ideas from geometry [14, 62] or physics [36]. It is more straightforward to incorporate regional properties of segments into implicit surface representation techniques like level-sets, which typically optimize geometric surface functionals related to continuous Mumford-Shah model [51].
All discrete path-based methods in group (B) can easily encode boundary-based segmentation cues. [33, 65] combine them with regional properties of segments using algorithms for optimizing some ratios of regional and boundary terms. Unfortunately, path-based methods are limited to 2D images since object boundaries in 3D cannot be represented by a path.
Graph cuts techniques in group (B) can optimize discrete energies that combine boundary regularization with regional consistency of segments in either 2D or 3D applications. The corresponding energies are consistent with the weak membrane model proposed by Blake and Zisserman [3, 5], which is a discrete counterpart of continuous Mumford-Shah functional [51]. As shown in [9, 40], graph cut methods can approximate the same geometric surface functionals that are widely used by level-set methods. This further bridges the gap between the weak membrane and Mumford-Shah models. Recently, [41] proposed parametric max-flow algorithm for optimizing ratios of some geometric functionals, extending some earlier ratio-based segmentation methods [33, 65] to applications in 3D.
1.5 Topological Constraints
Most segmentation methods using explicit boundary representation compute segmentation with fixed topological structure4, e.g. a single closed contour. Such methods typically have higher sensitivity to local minima. Moreover, object’s topology may not be known a priori. In contrast, most implicit representation methods produce segments with flexible topological structure. Object segment may have multiple isolated blobs with holes. Sometimes, however, it may help to impose topological constraints reflecting certain high-level contextual information about the object of interest.
Region-based topological constraints naturally fit into implicit methods (graph cuts, level-sets). These constraints correspond to an infinite cost regional bias that enforces certain pixels to belong to object’s interior or exterior. Similar ideas can also constrain the region of interest containing the object’s boundary. Typically, optimal segmentation can be efficiently recomputed if some regional constraints (seeds) are added or removed. [12] discusses some non-regional topological constraints that potentially could be used in the graph cut algorithms for object extraction. It is also possible to simultaneously segment multiple surfaces topologically coupled to each other, e.g. when distance between them is constrained to be in some interval [48]. This approach can be extended to elastic interaction between coupled surfaces using results in [31].
Note that intelligent scissors [50] and live wire [21] use boundary-based hard constraints where the user can indicate certain pixels where the segmentation boundary should pass. In contrast, regional hard constraints used for graph cuts do not have to be precisely positioned. Moving the seeds around the object of interest (within some limits) does not normally change the segmentation results.
2 Related work on Markov Random Fields
In this sections we review relationship between graph cut methods for object extraction and estimation of Markov Random Fields. Greig et al. [28] were first to recognize that powerful max-flow/min-cut algorithms from combinatorial optimization can be applied to problems in computer vision. In particular, they showed that graph cuts can be used for restoration of binary images.5 This problem can be formulated as Maximum A Posterior estimation of a Markov Random Field (MAP-MRF) that required minimization of posterior energy
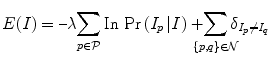
where
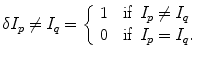 is a Kronecker delta representing interaction potential,
is a Kronecker delta representing interaction potential, 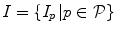 is an unknown vector of original binary intensities I p ∈ {0, 1} of image pixels
is an unknown vector of original binary intensities I p ∈ {0, 1} of image pixels  , vector
, vector 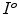 represents observed binary intensities corrupted by noise, and
represents observed binary intensities corrupted by noise, and 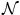 is a set of all pairs of neighboring pixels.
is a set of all pairs of neighboring pixels.
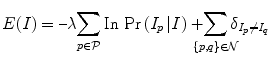
(1.1)
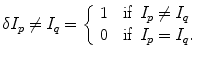
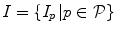 is an unknown vector of original binary intensities I p ∈ {0, 1} of image pixels
is an unknown vector of original binary intensities I p ∈ {0, 1} of image pixels 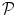 , vector
, vector 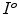 represents observed binary intensities corrupted by noise, and
represents observed binary intensities corrupted by noise, and 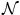 is a set of all pairs of neighboring pixels.
is a set of all pairs of neighboring pixels.Greig et al. [28] recognized that if I p ∈ {0, 1} for all 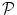 then posterior energy (1.1) is a typical example of energy of binary variables from pseudo-boolean optimization literature [29, 53]. In particular, [29, 53] show that minimization of such energies can be done by combinatorial algorithms for optimal graph partitioning. They show construction of a two terminal graph where the minimum cost cut divides the nodes (variables) into two disjoint sets corresponding to the globally optimal labeling of binary variables I p .
then posterior energy (1.1) is a typical example of energy of binary variables from pseudo-boolean optimization literature [29, 53]. In particular, [29, 53] show that minimization of such energies can be done by combinatorial algorithms for optimal graph partitioning. They show construction of a two terminal graph where the minimum cost cut divides the nodes (variables) into two disjoint sets corresponding to the globally optimal labeling of binary variables I p .
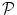 then posterior energy (1.1) is a typical example of energy of binary variables from pseudo-boolean optimization literature [29, 53]. In particular, [29, 53] show that minimization of such energies can be done by combinatorial algorithms for optimal graph partitioning. They show construction of a two terminal graph where the minimum cost cut divides the nodes (variables) into two disjoint sets corresponding to the globally optimal labeling of binary variables I p .
then posterior energy (1.1) is a typical example of energy of binary variables from pseudo-boolean optimization literature [29, 53]. In particular, [29, 53] show that minimization of such energies can be done by combinatorial algorithms for optimal graph partitioning. They show construction of a two terminal graph where the minimum cost cut divides the nodes (variables) into two disjoint sets corresponding to the globally optimal labeling of binary variables I p .Greig et al. [28] were first to compute globally optimal results for MAP-MRF estimation on 2D images. Previously, energies like (1.1) were approached with iterative sampling algorithms like simulated annealing. In fact, Greig et al. mainly used their results to show that in practice simulated annealing reaches solutions very far from the global minimum even in very simple binary image restoration examples.
Unfortunately, the graph cut approach to MAP-MRF estimation in [28] remained unnoticed for almost 10 years mainly because binary image restoration looked very limited as an application. In the late 90’s new computer vision techniques appeared that showed how to use graph cut algorithms for more interesting non-binary problems. [57] was the first to use graph cuts to compute multi-camera stereo. Later, [31] showed that with the right edge weights on a graph similar to [57] one can globally minimize a non-binary case of (1.1) with any convex pairwise interaction terms, e.g. L 1 or L 2 metrics on the space of labels. Other algorithms for convex or even more general class of (multi-label) submodular interactions were also discovered. A different case of multi-label energies where the interaction penalty (metric) is not-necessarily convex was studied in [13]. In general, this is an NP-hard problem. The α-expansion algorithm proposed in [13] finds provably good approximate solutions by iteratively running min-cut/max-flow algorithms on appropriate graphs. The general case of metric includes “truncated” interaction potentials, also known as discontinuity preserving, which is practically very important for solving image analysis problems, e.g. [3, 5]). Later, it was shown that iterative α-expansion technique can be also used for non-metric interactions [55, 43] while further weakening optimality guarantees.
One of the insights in [8, 7] was that the problem of segmenting an object of interest from its background can be formulated as a binary image labeling problem and that an energy similar to (1.1) can be useful for object extraction. For example, binary image restoration energy (1.1) contains two terms representing “regional” and “boundary” properties. Such a combination looks appropriate for object segmentation. Moreover, this energy can be globally minimized in N-D images/volumes using combinatorial graph cut algorithms as suggested in pseudo-boolean optimization literature. [8, 7] showed how to integrate various basic cues and constraints in order to extract objects of interest.
3 Optimal object segmentation via graph cuts
This section describe basic MRF object segmentation framework in more detail. First, consider some terminology. A graph 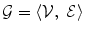 is defined as a set of nodes or vertices
is defined as a set of nodes or vertices 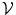 and a set of edges
and a set of edges 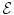 connecting “neighboring” nodes. For simplicity, we mainly concentrate on undirected graphs where each pair of connected nodes is described by a single edge
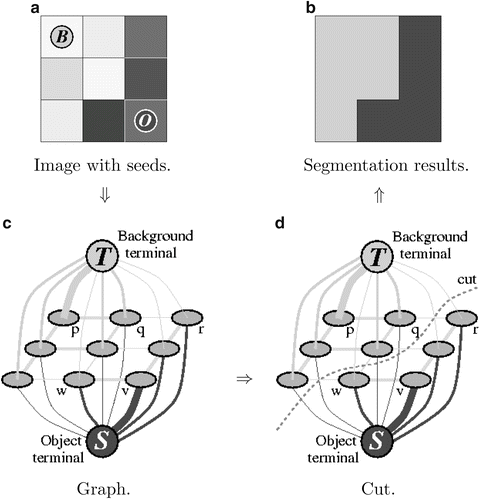
connecting “neighboring” nodes. For simplicity, we mainly concentrate on undirected graphs where each pair of connected nodes is described by a single edge 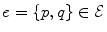 6. A simple 2D example of an undirected graph that can be used for image segmentation is shown in Fig. 2(b).
6. A simple 2D example of an undirected graph that can be used for image segmentation is shown in Fig. 2(b).
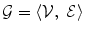 is defined as a set of nodes or vertices
is defined as a set of nodes or vertices 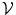 and a set of edges
and a set of edges 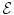 connecting “neighboring” nodes. For simplicity, we mainly concentrate on undirected graphs where each pair of connected nodes is described by a single edge
connecting “neighboring” nodes. For simplicity, we mainly concentrate on undirected graphs where each pair of connected nodes is described by a single edge 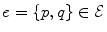 6. A simple 2D example of an undirected graph that can be used for image segmentation is shown in Fig. 2(b).
6. A simple 2D example of an undirected graph that can be used for image segmentation is shown in Fig. 2(b).