All matter is composed of individual entities called elements. Each element is distinguishable from the others by the physical and chemical properties of its basic component—the atom. Originally thought to be the “smallest” and “indivisible” particle of matter, the atom is now known to have a substructure and can be “divided” into smaller components. Each atom consists of a small central core, the nucleus, where most of the atomic mass is located, and a surrounding “cloud” of electrons moving in orbits around the nucleus. Whereas the radius of the atom (radius of the electronic orbits) is approximately 10^-10 m, the nucleus has a much smaller radius, namely about 10^-15 m. Thus, for a particle of size comparable to nuclear dimensions, it will be quite possible to penetrate several atoms of matter before a collision happens. As will be pointed out in the chapters ahead, it is important to keep track of those particles that have not interacted with the atoms (the primary beam) and those that have suffered collisions (the scattered beam).

The properties of atoms are derived from the constitution of their nuclei and the number and the organization of the orbital electrons.

The nucleus contains two kinds of fundamental particles: protons and neutrons. Whereas protons are positively charged, neutrons have no charge. Because the electron has a negative unit charge (1.60 × 10^-19 Coulombs) and the proton has a positive unit charge, the number of protons in the nucleus is equal to the number of electrons outside the nucleus, thus making the atom electrically neutral.

An atom is completely specified by the formula ^A_ZX, where X is the chemical symbol for the element; A is the mass number, defined as the number of nucleons (neutrons and protons in the nucleus); and Z is the atomic number, denoting the number of protons in the nucleus (or the number of electrons outside the nucleus). An atom represented in such a manner is also called a nuclide. For example, ¹₁H and ⁴₂He represent atoms or nuclei or nuclides of hydrogen and helium, respectively.

On the basis of different proportions of neutrons and protons in the nuclei, atoms have been classified into the following categories: isotopes, atoms having nuclei with the same number of protons but different number of neutrons; isotones, having the same number of neutrons but different number of protons; isobars, with the same number of nucleons but different number of protons; and isomers, containing the same number of protons as well as neutrons. The last category, namely
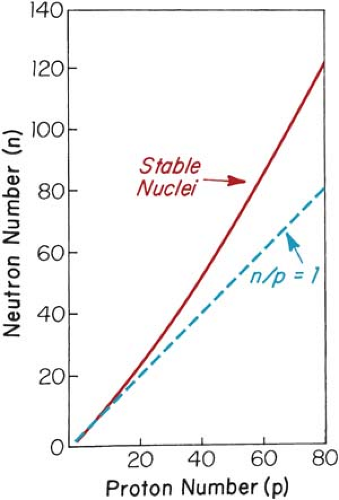
isomers, represents identical atoms except that they differ in their nuclear energy states. For example, ^131μ₅₄Xe (μ stands for metastable state) is an isomer of ¹³¹₅₄Xe. Certain combinations of neutrons and protons result in more stable (nonradioactive) nuclides than others. For instance, stable elements in the low-atomic-number range have an almost equal number of neutrons, N, and protons, Z. However, as Z increases beyond about 20, the neutron-to-proton ratio for stable nuclei becomes greater than 1 and increases with Z. This is evident in Figure 1.1, which shows a plot of the ratios of neutrons to protons in stable nuclei.

Nuclear stability has also been analyzed in terms of even and odd numbers of neutrons and protons. Of about 300 different stable isotopes, more than half have even numbers of protons and neutrons and are known as even-even nuclei. This suggests that nuclei gain stability when neutrons and protons are mutually paired. On the other hand, only four stable nuclei exist that have both odd Z and odd N, namely ²₁H, ⁶₃Li, ¹⁰₅B, and ¹⁴₇N. About 20% of the stable nuclei have even Z and odd N and about the same proportion have odd Z and even N.

Masses of atoms and atomic particles are conveniently given in terms of atomic mass unit (amu). An amu is defined as one twelfth of the mass of a ¹²₆C atom, a carbon isotope. Thus, the atom of ¹²₆C is arbitrarily assigned the mass equal to 12 amu. In basic units of mass:

The mass of an atom expressed in terms of amu is known as atomic mass or atomic weight. Another useful term is gram atomic weight, which is defined as the mass in grams numerically equal to the atomic weight. According to Avogadro’s law, every gram atomic weight of a substance contains the same number of atoms. The number, referred to as Avogadro’s number (N_A), has been measured by many investigators, and its currently accepted value is 6.0228 × 10²³ atoms per gram atomic weight.

From the previous definitions, one can calculate other quantities of interest such as the number of atoms per gram, grams per atom, and electrons per gram. Considering helium as an example, its atomic weight (A_W) is equal to 4.0026.

Therefore:

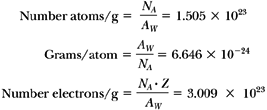
The masses of atomic particles, according to the atomic mass unit, are electron = 0.000548 amu, proton = 1.00727 amu, and neutron = 1.00866 amu.

Because the mass of an electron is much smaller than that of a proton or neutron and protons and neutrons have nearly the same mass, equal to approximately 1 amu, all the atomic masses in units of amu are very nearly equal to the mass number. However, it is important to point out that the mass of an atom is not exactly equal to the sum of the masses of constituent particles. The
reason for this is that, when the nucleus is formed, a certain mass is destroyed and converted into energy that acts as a “glue” to keep the nucleons together. This mass difference is called the mass defect. Looking at it from a different perspective, an amount of energy equal to the mass defect must be supplied to separate the nucleus into individual nucleons. Therefore, this energy is also called the binding energy of the nucleus.

The basic unit of energy is the joule (J) and is equal to the work done when a force of 1 newton acts through a distance of 1 m. The newton, in turn, is a unit of force given by the product of mass (1 kg) and acceleration (1 m/sec²). However, a more convenient energy unit in atomic and nuclear physics is the electron volt (eV), defined as the kinetic energy acquired by an electron in passing through a potential difference of 1 V. It can be shown that the work done in this case is given by the product of potential difference and the charge on the electron. Therefore, we have:

Multiples of this unit are:

According to Einstein’s principle of equivalence of mass and energy, a mass μ is equivalent to energy E and the relationship is given by:

where c is the velocity of light (3 ÷ 10⁸ m/sec). For example, a mass of 1 kg, if converted to energy, is equivalent to:

The mass of an electron at rest is sometimes expressed in terms of its energy equivalent (E₀). Because its mass is 9.1 × 10^-31 kg, we have from Equation 1.1:

Another useful conversion is that of amu to energy. It can be shown that:

From Equation 1.1 we can see that the equivalent mass of any particle of total energy E (kinetic plus rest mass energy) is given by E/c². Accordingly, masses of particles may also be expressed in units of GeV/c². It can be shown that:

According to the model proposed by Niels Bohr in 1913, the electrons revolve around the nucleus in specific orbits and are prevented from leaving the atom by the centripetal force of attraction between the positively charged nucleus and the negatively charged electron.

On the basis of classical physics, an accelerating or revolving electron must radiate energy. This would result in a continuous decrease of the radius of the orbit with the electron eventually spiraling into the nucleus. However, the data on the emission or absorption of radiation by elements reveal that the change of energy is not continuous but discrete. To explain the observed line spectrum of hydrogen, Bohr theorized that the sharp lines of the spectrum represented electron jumps from one orbit down to another with the emission of light of a particular frequency or a quantum of energy. He proposed two fundamental postulates: (a) electrons can exist only in those orbits for which the angular momentum of the electron is an integral multiple of h/2p, where h is the Planck’s constant (6.62 × 10^-34 J-sec); and (b) no energy is gained or lost while the electron remains in any one of the permissible orbits.

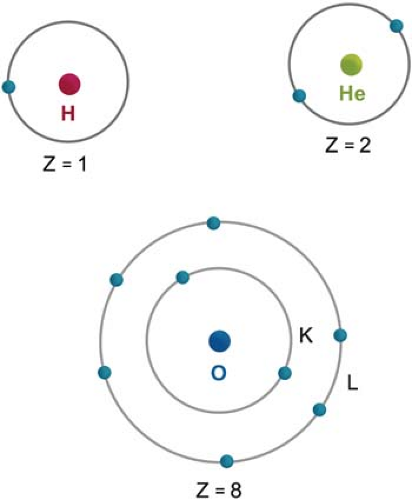
The arrangement of electrons outside the nucleus is governed by the rules of quantum mechanics and the Pauli exclusion principle (not discussed here). Although the actual configuration of electrons is rather complex and dynamic, one may simplify the concept by assigning electrons to specific orbits. The innermost orbit or shell is called the K shell. The next shells are L, M, N, and O. The maximum number of electrons in an orbit is given by 2n², where n is the orbit number. For example, a maximum of two electrons can exist in the first orbit, eight in the second, and 18 in the third. Figure 1.2 shows the electron orbits of hydrogen, helium, and oxygen atoms.

Electron orbits can also be considered as energy levels. The energy in this case is the potential energy of the electrons. With the opposite sign it may also be called the binding energy of the electron.

It is customary to represent the energy levels of the orbital electrons by what is known as the energy level diagram (Fig. 1.3). The binding energies of the electrons in various shells depend on the magnitude of Coulomb force of attraction between the nucleus and the orbital electrons. Thus, the binding energies for the higher-Z atoms are greater because of the greater nuclear charge. In the case of tungsten (Z = 74), the electrons in the K, L, and M shells have binding energies of about 69,500, 11,000, and 2,500 eV, respectively. The so-called valence electrons, which are responsible for chemical reactions and bonds between atoms as well as the emission of optical radiation spectra, normally occupy the outer shells. If energy is imparted to one of these valence electrons to raise it to a higher-energy (higher potential energy but lower binding energy) orbit, this will create a state of atomic instability. The electron will fall back to its normal position with the emission of energy in the form of optical radiation. The energy of the emitted radiation will be equal to the energy difference of the orbits between which the transition took place.