Fig. 4.1
The electromagnetic spectrum is illustrated. Therapeutic X-ray or ionizing radiation is in the energy range of 105 eV and higher. The energy of photon beams commonly used in radiosurgery are higher than 106 eV
Protons, defined as positively charged particles found in the nucleus of an atom, are also used for treatment [15–19]. Proton beams can be obtained from particle accelerators such as cyclotrons and synchrotrons [20], which cost a tremendous amount of money; thus, very few proton facilities exist worldwide, and there are currently only five in the USA.
Because the majority of radiosurgery treatments are performed with photon beams, emphasis is placed on the photon beam.
Cobalt-60
Cobalt-60 is the radioactive isotope used as the radiation source in the Leksell Gamma Knife treatment machine (Elekta. Nor-cross, GA), which is described later. A radioactive isotope is an atom with an unstable nucleus that tries to stabilize itself through a process called radioactive decay by emitting ionizing radiation such as alpha, beta, and/or gamma particles. When 60Co undergoes radioactive decay, it emits beta particles and two strong gamma radiations, one with 1.17 MeV of energy and the other with 1.33 MeV of energy (Fig. 4.2). MeV, a commonly used unit of energy for particles in the treatment energy range, means 1 million electron volts, where 1 electron volt is the energy gained by an electron that accelerates through a potential difference of 1 V. A real treatment beam of Gamma Knife can include photons of energy different from 1.17 and 1.33 MeV because some photons experience interactions with 60Co itself and/or its capsulation material and lose a part of that energy. Therefore, the effective energy of Gamma Knife is slightly lower than 1.25 MeV (the average of 1.17 and 1.33 MeV).
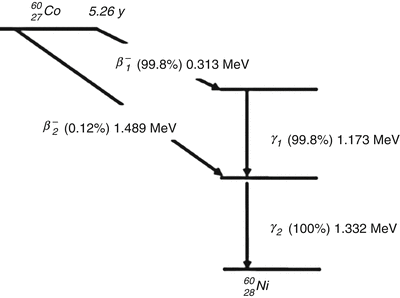

Fig. 4.2
For 60Co, most of the disintegrations (99.8 %) are the emission of a β 1− with a maximum energy of 0.313 MeV. This leads to an excitation of 60Ni, which releases its energy quickly by emitting two gamma rays (1.173 and 1.332 MeV) in cascade. In some disintegration (0.12 %), a β 2− particle with a maximum energy of 1.486 MeV is released and leads to the lowest excited state of 60Ni
Cobalt-60 ultimately decays to nonradioactive nickel. The half-life of 60Co, that is, the length of time needed for 60Co to lose half of its radioactivity from decay, is 5.26 years. At the end of 1 half-life, only 50 % of the original radioactive material remains. This means that treatment time after 5 years is double that at the time of initial installation, and that the source of Gamma Knife needs to be replaced after a certain period of time to avoid long treatment times.
X-Ray Production in a Linear Accelerator
One of the interesting characteristics of a fast-moving electron is that when it interacts with a material, it can produce an X-ray. A part or whole of the kinetic energy of the electron is transformed into electromagnetic energy. This principle is used to obtain X-rays in most X-ray production machines in which electrons are accelerated and induced to hit a target and then generate an X-ray. The amount of X-ray particles produced increases as the kinetic energy of the incident electrons increases. Electrons are accelerated by potential differences in diagnostic X-ray tubes up to several hundred kiloelectron volts (keV). The acceleration mechanism in a linear accelerator, however, is somewhat different because it uses microwave technology similar to that used for radar to accelerate electrons in a linear tube, often called an accelerator tube [21]. In linear accelerators, electrons are usually accelerated to the energy range of 4–25 MeV. A 6-MeV electron is most often used to create an X-ray for radiosurgery. When an electron creates a photon, theoretically, the photon can take any energy from 0 to the same as the energy of the incident electron. In other words, the photon beam produced by a 6-MeV electron beam can have an energy spectrum of 0–6 MeV. The energy of an X-ray produced in a linear accelerator is denoted MV instead of MeV. The major components and auxiliary systems of typical medical linear accelerators are shown in a block diagram (Fig. 4.3). The role of each part is briefly explained below.
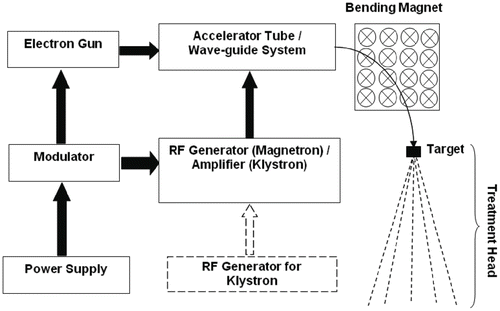

Fig. 4.3
The power supply provides DC to the modulator, which provides a high-voltage pulse to the RF generator and electron gun simultaneously. The electron gun introduces the electron in pulse to the accelerator tube. Electron production occurs through the thermionic process. The RF generator introduces a microwave to the accelerator tube. The electron and the microwave are timed exactly to be met in the accelerator tube by the modulator. The accelerator tube accelerates the electrons via the resonance cavity. As the accelerated electron comes out of the accelerator tube, the path of the electron is bent through a bending magnet to hit the target and generates an X-ray
Power Supply
The power supply provides direct current (DC) power to the modulator.
Modulator
The modulator generates high-voltage pulses lasting a few microseconds that are simultaneously introduced to the radiofrequency source and the electron gun.
Electron Gun
The electron gun produces electrons by thermionic emission. In a conducting material, the electrons exist at or below the baseline electron energy at low temperatures. As the temperature is increased, some of these electrons have sufficient energy to pass over the surface–potential barrier between the material and the vacuum. This process of increasing the temperature of a bulk material to increase the number of electrons that can leave the material is called thermionic emission. These electrons are pulse-injected into the accelerator tube according to the signal from the modulator.
Radiofrequency Source
Radiofrequency (RF) is a range of electromagnetic frequencies above sound and below visible light, generally in the 30 kHz to 300 GHz range. RF is used for all broadcast transmissions including AM and FM radio, television, shortwave, microwave, and satellite transmissions. In a linear accelerator used for radiosurgery, a magnetron is often the RF source. The magnetron is a diode-type electron tube that functions as a high-power oscillator to generate microwave pulses. Pulse duration is several microseconds long, and the repetition rate is several hundred pulses per second. Following the pulses from the modulator, microwave pulses are introduced into the accelerator tube through the waveguide system. The typical frequency of microwaves used in a linear accelerator is about 3 GHz.
In some designs, a klystron is used instead of a magnetron. The klystron is a microwave amplifier rather than a source; therefore, it requires a low-power microwave oscillator called an RF driver as an RF source. In general, a klystron produces microwaves of higher power than the magnetron and is often used with high-energy linear accelerators (>10 MV).
Waveguide System
The waveguide system is made up of a pressurized rectangular tube through which microwave pulses generated by either a magnetron or klystron are transmitted into the accelerator tube.
Accelerator Tube
An accelerator tube consists of many RF resonant cavities. An RF cavity allows power to be coupled into the particle beam. In an electron linear accelerator, RF accelerating cavities are basically microwave resonators. Resonance is a very common physical phenomenon that can be observed in many types of systems. Imagine a child on a swing, for example. If the child pushes the swing at just the right time, the push can make the swing go higher and higher with very little effort. The swing has a natural frequency of oscillation. Pushing “at just the right time” means that energy is put into the system at a frequency known as the fundamental frequency. Now the system is said to be in resonance condition.
The amplitude of the motion can increase rapidly with resonance. An analogous phenomenon can occur in a linear accelerator with RF resonance, which is generally derived from an RF cavity that is typically in a right circular cylindrical shape with connecting holes to allow a charged particle’s beam to pass through for acceleration. Figure 4.4 shows a typical cylindrically symmetric RF cavity. In a fundamental RF mode, the electric field is roughly parallel to the beam axis and radically decays to zero upon approach to the cavity walls. The pulsed electron particle beam traverses the cavity through the centered hole, creating an accelerating force along the axis of the cavity due to the electric field.


Fig. 4.4
A typical cylindrically symmetric cavity
Bending Magnet
When an electron moves in a magnetic field, it experiences force. The direction of the force is at right angles to both the direction of the magnetic field and the direction of the electron motion (Fig. 4.5). Using this principle, the path of accelerated electrons is controlled so that they can hit the target normally (note the electron path, bending magnet, and target in Fig. 4.3). Magnets used for this purpose are called bending magnets. In certain cases, straight-ahead beam designs can be applied without the bending magnet if the acceleration structure is short enough to be placed in a vertical direction. A linear accelerator in straight-ahead beam design is used in the CyberKnife unit, which will be better described later.


Fig. 4.5
As the electron travels into a uniform magnetic field, it experiences a downward force. This force causes the electron to travel in a circular path. The crosses in the figure indicate the uniform magnetic field pointing into the page
Treatment Head
The major parts of the treatment head are the target (often called the X-ray target), primary collimator, flattening filter, ion chamber, and secondary collimators (Fig. 4.6).


Fig. 4.6
A schematic of the treatment head of a medical linear accelerator is illustrated. Initially, as the accelerated electrons hit an X-ray target, an X-ray beam is generated via the bremsstrahlung process. This X-ray beam is collimated by the primary collimator. As it exits the primary collimator, the X-ray beam profile is flattened out by the flattening filter. Then, it goes through the ion chamber, and, finally, it gets collimated by the secondary collimator. In radiosurgery, generally one more collimator is added to make a very small field (e.g., circular collimator or micro-multileaf collimator)
Accelerated electrons collide with the target to generate an X-ray beam. For a given energy of electrons, more X-rays can be produced if a target material with a higher atomic number (Z number) is used. Tungsten and gold are commonly used as target materials.
The production of an X-ray is based on a process called bremsstrahlung (meaning “braking radiation”), which is the result of radiative collisions between a fast-moving electron and a nucleus. When the electron passes near a nucleus, it can be deflected from its path by Coulomb forces of attraction and lose its energy as bremsstrahlung radiation (i.e., an X-ray). The X-rays are produced in all directions, but high-energy X-rays are produced in the forward direction (Fig. 4.7). Therefore, in a linear accelerator, higher photon intensity is observed in the area close to the central line (i.e., the extended line following the direction of the incident electron) below the X-ray target. The X-ray beam is first collimated by the primary collimator, which has a circular aperture through which a photon beam can pass to make a radiation field. The primary collimator is typically made of tungsten.


Fig. 4.7
Schematic illustration of the angular distribution of emission of bremsstrahlung X-rays around a target. At the kinetic energy of an electron beam less than 100 keV, X-rays are emitted relatively equally in all directions. As the kinetic energy of the electron beam increases, the direction of the bremsstrahlung X-ray emission becomes significantly forward. In megavoltage X-ray machines, the transmission X-rays are therefore used to treat a patient
For patient treatment, a radiation beam with uniform intensity across the field is desirable, and to create a uniform photon beam, a conical filter called a flattening filter is used. The central area of the flattening filter is thicker to attenuate more photons in the central area. In general, a high-Z-number material is used for the flattening filter to effectively attenuate photons.
The amount of radiation produced by the linear accelerator is monitored by an ionization chamber, often called a monitor chamber. The monitor chamber not only controls the amount of radiation delivered to the patient but also checks and controls the uniformity of the delivered radiation.
Whereas the primary collimator defines the maximum aperture of the radiation field, a real treatment field is determined by the secondary collimator, which defines a rectangular field that fits to each patient treatment in routine radiation therapy. In radiosurgery, smaller fields are needed. Thus, an additional collimator system, either a circular collimator or micro-multileaf collimator (mMLC) [22], is used.
Flattening Filter Free Mode
As described before, photon beams produced in a conventional linear accelerator by bombarding a high-Z target with accelerated electrons are strongly forward peaked (see Fig. 4.7), resulting in significant centrally peaked fluence distributions incident to patients. In the past, such a nonuniform fluence was considered not suitable for routine clinical applications and intentionally flattened by a flattening filter (FF) as shown in Fig. 4.6. However, the rationale that a FF is required to obtain uniform dose distributions is getting less strong in modern radiation therapy. An example is the so-called intensity modulated radiation therapy (IMRT), one of the most significant advancements in modern radiation therapy. In IMRT, highly inhomogeneous beam fluences are often applied to achieve extremely conformal dose distributions even to concave targets, implying no need of flattened beam in principle. Another example is in case of relatively small field treatments such as stereotactic radiosurgery (SRS), stereotactic radiotherapy (SRT), and stereotactic body radiotherapy (SBRT) because there is no significant difference in beam fluence profile across the field between flattened and unflattened beams when field sizes are small. Thus, flattening filter free (FFF) mode is available in several state-of-the-art commercial linear accelerators nowadays.
The major advantage of a FFF beam is significantly large dose rate compared to conventional flattened beams [23]. With larger dose rate, treatment time can be reduced and uncertainty related to patient motion may become smaller. This feature is very important especially for SRS, SRT, and SBRT where fractional dose is large. Figure 4.8 shows dose rate profiles at 10 cm depth of water in several field sizes, 4×4 cm2 (a), 6×6 cm2 (b), and 8×8 cm2 (c), for both regular flattened 6 MV beam and 6 MV FFF beam from a Varian TrueBeam linear accelerator. As can be seen, dose rates in FFF mode are larger than those in regular flattened beams by about two times in 6 MV while profiles are not much different. Dose rates in FFF mode become about four times larger in 10 MV but more nonuniform dose profiles are expected.


Fig. 4.8
Dose rate profiles at 10 cm depth of water in three field sizes, 4 × 4 cm2 (a), 6 × 6 cm2 (b), and 8 × 8 cm2 (c), for both regular flattened 6 MV beam (denoted as 6 MV) and 6 MV FFF beam from a Varian TrueBeam linear accelerator. Dose rate scale is arbitrary and as illustrated, dose rates in FFF mode are larger than those in regular flattened beams by about two times while profiles are not much different
A Photon’s Interaction with Matter
The effectiveness of radiation treatment is based on how much radiation energy is deposited in the tumor compared with the energy deposited in the surrounding normal tissues. Energy deposition occurs through interactions between a radiation beam and the human body at either the atomic or nuclear level. When photons traverse a material, they reduce the intensity of the incident photons. The three most common ways for a photon to interact with matter for energies above a few keV are photoelectric absorption, Compton scattering, and pair production. These three mechanisms account for more than 99 % of the interactions between photons and matter, and the probability of each depends on the energy of the photon and the material with which it interacts. Because these interactions are quantum in nature, a specific interaction is never guaranteed. It is simply more or less probable than the others (depending on the energy and the material).
Photoelectric Absorption
In photoelectric absorption, an X-ray photon is absorbed by the interacting material and an electron from a shell of the atom is ejected, leaving the atom ionized, as illustrated in Fig. 4.9. The ionized atom returns to the neutral state with the emission of an X-ray, called the characteristic X-ray of the atom. The kinetic energy transferred to the ejected electron during the interaction is the same as the incident photon energy minus the ejected electron’s binding energy to the atomic nucleus. Photoelectric absorption occurs predominately at low energies of photons and for high-atomic-number materials. In water (one of the closest materials to tissue), the probability of this interaction becomes negligible once photon energy reaches above 100 keV. Because the effective energies of photon beams from the Gamma Knife (i.e., 60Co source) and linear accelerator are of the order MeV, the effect of photoelectric absorption is not significant in radiosurgery.


Fig. 4.9
In a photoelectric effect, an incident photon striking a bounded electron is absorbed, and the electron is ejected from the atom with a kinetic energy equal to the difference between the incident photon energy and the binding energy of the electron. The probability of the photoelectric effect increases as the atomic number of the target material increases; however, it decreases as the energy of the incident photon increases. (E is the energy of the incident photon, T is the kinetic energy of the ejected electron, and BE is the binding energy. Photon energy is expressed as hν, where h is Plank’s constant and ν is frequency)
Compton Scattering
In Compton scattering, also known as an incoherent scattering, the incident X-ray photon ejects an electron from an atom, loses some of its energy to the ejected electron, and continues to move in a direction different from the initial direction. The resulting incident photon is called a scattered photon, whereas it is called a primary photon before the interaction. The energy and momentum are conserved in this process. Kinetic energy transferred to the electron is the energy difference between the primary and scattered photons. The energy of the scattered photon depends on the direction (i.e., the angle with respect to the direction of the primary photon). The scattered photon has minimal energy when it is backscattered (180° from its direction of travel). If it is scattered in the same direction as the primary, the scattered photon energy is the same as the primary photon energy. Compton scattering is important for low-atomic-number materials and photon energies of 100 keV to 10 MeV. Therefore, Compton scattering is the most significant interaction for photons used in radiosurgery. Figure 4.10 illustrates the Compton scattering interaction.


Fig. 4.10
In Compton scattering, the incident photon strikes an electron and ejects it out of the atom to which it was bound. During this process, the incident photon energy is transferred to the ejected electron. The least energy is transferred to the electron when the incident photon has no scattering (i.e., θ = 0º), and the most energy is transferred to the electron when the incident photon is scattered backward (i.e., θ = 180º). Compton scattering becomes most significant at an energy range of 100 keV to 10 MeV, and it is almost independent of the atomic number (i.e., Z value) of the interacting material. Thus, for the radiosurgery energy range, Compton scattering is the dominating interaction. (E is the energy of the incident photon. T is the kinetic energy of the ejected electron, and E′ is the energy of the scattered photon)
Pair Production
Photons have a quantum of energy but zero mass. In pair production, the incident photon energy is completely absorbed in the medium, and an electron and its antiparticle, a positive electron called a positron, are created. This interaction is illustrated in Fig. 4.11. Pair production can only occur when the energy of the incident photon is greater than 1.02 MeV, which is the minimum energy needed to create an electron and a positron. Positrons are very short lived and disappear with the creation of two 0.51-MeV photons each, a process called positron annihilation. The total kinetic energy transferred to the electron and positron pair is equal to the incident photon energy minus 1.02 MeV. Pair production is of particular importance when high-energy photons pass through materials of a high atomic number but plays a small role in photon beams used for radiosurgery.


Fig. 4.11
When a photon with energy equal to or higher than 1.02 MeV comes very close to the nucleus of an atom, it interacts with the nuclear Coulombic force field and can create a pair of an electron and a positron. The total kinetic energy of the electron and position is the energy of the incident photon minus 1.02 MeV. The probability of pair production is proportional to the atomic number of the target material and the incident photon energy
Dose and Dosimetry
The physical quantity that is used in radiation therapy to kill neoplastic cells is the kinetic energy of the incident radiation beam. Once photons enter a medium, they start to interact with the medium with the probability of interactions described earlier. Any photon particle loses a part or all of its energy when it initially interacts with a medium and most of the lost energy is absorbed by the medium around the interaction point. Energy absorbed in a unit mass of the interaction medium during interactions with a radiation beam is called the dose or, more specifically, the radiation dose. The commonly used unit of dose is the gray (Gy), which is equivalent to J/kg (joules per kilogram), where joule is a unit of energy (1 J is the approximate energy required to lift 1 kg by 0.1 m assuming gravity accelerates at 10 m/s2). Depending on the amount of dose, cGy (centigray, or one-hundredth of a Gy) is also often used. Dosimetry is either the measuring or calculating of dose.
As you may have noted, the energy absorption mechanism during photon interaction is a two-step process: (1) energy transfers from the photon to the ejected electron and (2) energy is deposited from the ejected electron to the medium (Fig. 4.12). Thus, energy deposition occurs within a volume around the spot of interaction rather than at a point of interaction. If the photon still has kinetic energy after the first interaction (e.g., Compton scattering), it can travel and interact at another point, then cause another energy deposition. This second interaction is independent of the first interaction, thus, third, fourth, and multiple scatterings are possible. The energy absorbed from scattered photons is called the scattered dose, contrary to the primary dose, which is the energy absorbed in the first interaction. The same thing happens when a patient is irradiated with a photon beam. Photons interact with human tissue and deposit energy into the tissue. Radiation therapy’s aim is to kill the target tissue (or cell) through enough impact from the energy deposition while minimizing the impact to the normal tissue. In other words, local control of treatment depends on how much dose is delivered to the target (and how accurately, too, of course), and normal tissue complication is dependent on how much unwanted dose is given to the normal structure.


Fig. 4.12
A photon enters a volume of a medium and transfers a portion of its energy, thus giving the electron a kinetic energy. The electron will travel a short distance and deposit its energy in a medium. The original photon will continue to travel within the medium as it transfers more energy to another electron
There are two commonly used dose-calculation methods: measurement based and model based. Measurement-based approaches directly use dose distributions measured in phantoms. On the other hand, model-based approaches try to calculate the dose from the first principles with limited use of measured data.
Measurement-Based Dose Calculation
Dose calculation is mainly based on three parameters: percent depth dose (PDD), profile, and output.
Percent Depth Dose
When a photon beam is incident on a medium, it creates a dose distribution within the medium. Relative dose at any depth is called the depth dose (DD) and when it is expressed as a percentile it is called the PDD. Let us assume a certain number of photons in a hypothetical narrow beam are incident on a thin medium (Fig. 4.13a). The number of photons decreases exponentially because some photons interact with the medium and disappear from the path of the narrow beam. Now think of energy deposition (i.e., dose) at depth. The absorbed dose is proportional to the amount of radiation interactions. Energy, however, is deposited by ejected electrons rather than by photons themselves. Because most of the ejected electrons lose energy continuously while traveling through the medium, there is a distance lag between the photon interactions and the dose. This mechanism also creates a so-called build-up region in the shallow depth of the medium. Although the number of interactions is the highest at the surface of the medium, dose is almost zero (because most ejected electrons move deeper into the medium). Thus, dose is close to zero at the surface, starts to build up with depth, and reaches the maximum. Then, the dose begins to decrease exponentially. Figure 4.14 shows a typical shape of DD (or PDD) for a narrow beam. In reality, the target volume is finite in size (Fig. 4.13b). In this scenario, some of the scattered photons can scatter back to the center of the field and contribute to the dose at depth. This effect is minimal, however.



Fig. 4.13
(a) In the thin line of beam and thin medium, the scattered photons are out of the medium and never return back to the medium. There is thus no contribution by the scattered photons to the dose. Percent depth dose (PDD) is mainly determined by the energy deposition of the primary photons. (b) On the other hand, in the thick medium with the thin line of photon beam, the scattered photons can further interact with the medium and return to the center line of PDD measurement. In general, however, this effect is insignificant. (c) In the broad beam and thick medium, the single or multiple scattering of photons can occur at any line of beam. The broad beam is considered as a bundle of thin lines of beam. The scattered photons coming from each beam line to the center line of interest contribute to the total dose. PDD values beyond the d max (depth of dose maximum) increase with field size because there are more line beams for larger fields. Because most radiosurgery fields are small, radiosurgery beams are close to case (b)

Fig. 4.14
A typical PDD with a narrow beam is illustrated. The dose is close to zero at the surface and starts to build up with depth until reaching the maximum. This region is called the build-up region. After the depth of dose maximum, it then begins to decrease exponentially. Note that depth dose (DD) is displayed in the “log” scale whereas depth is in the “linear” scale (i.e., log–linear plot). In a log–linear plot, an exponential decrease is expressed as a line
The scatter effect is significantly enhanced with a broad beam (Fig. 4.13c) because more scattered photons can contribute to the dose. The chance of multiple scattered photons coming to the central line increases with field size because more scattered photons exist in a larger field, so PDD increases with field size (Fig. 4.15). In radiosurgery, however, most fields are relatively small, so the scatter effect is insignificant. Thus, most radiosurgery beams are similar to the case shown in Fig. 4.13b, and PDD can be analytically expressed as a simple exponential function.


Fig. 4.15
Comparison of PDD curves for various field sizes. As the depth gets deeper, PDD increases with field size because of the increased amount of scatter dose contribution. Note that it is intentionally shown in “linear–linear” scale to illustrate that PDD is often drawn in two ways, “linear–linear” and “log–linear” (see Fig. 4.13)
Profile or Off-Axis Ratio
Figure 4.16 shows an ideal dose profile, often called the off-axis ratio (OAR), in a plane where a certain amount of dose is given uniformly inside the field and no dose is deposited outside the field. In reality, it is not possible to obtain such a profile. A typical dose profile in a plane at a certain depth for a clinical radiation beam is shown in Fig. 4.17a. The dose is uniform in the central area but starts to gradually decrease as it nears the field edge. It then drops rapidly at the geometric edge of the field and slowly approaches zero dose (<1 %) away from the field edge. The region of rapid dose fall-off is called the penumbra. When a field is large, the flat plateau in the central area is clearly observed. As the field size becomes smaller, the plateau disappears as illustrated in Fig. 4.17b, which is a profile for a typical radiosurgery beam. In radiosurgery, most radiation fields (<50 mm in diameter) show either no plateau region or a very narrow plateau region. Because of the large dose variation within a small region, a high-resolution measurement detector is required for dose profile measurement [24–30]. The shape of the individual radiation field is defined by the collimator system that is specifically based on the radiosurgery delivery system.



Fig. 4.16
An ideal dose profile in a plane is illustrated

Fig. 4.17
(a) A typical dose profile is illustrated for a conventional beam. The region of rapid dose change is called the penumbra. (b) A typical dose profile for a radiosurgery beam
Output
The magnitude of radiation produced by the delivery system is called the output. In general, this is a relative value that is normalized to the output of a reference field size. Output varies with field size (or collimator size). Larger field sizes have higher output.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree