Shielding blocks are most commonly made of lead. The thickness of lead required to provide adequate protection of the shielded areas depends on the beam quality and the allowed transmission through the block. A primary beam transmission of 5% through the block is considered acceptable for most clinical situations. If n is the number of half-value layers to achieve this transmission:

or:

or:

or:

Thus, a thickness of lead between 4.5 and 5.0 half-value layers would give less than 5% primary beam transmission and is, therefore, recommended for most clinical shielding.

Shielding against primary radiation for superficial and orthovoltage beams is readily accomplished by thin sheets of lead that can be placed or molded on to the skin surface. However, as the beam energy increases to the megavoltage range, the thickness of lead required for shielding increases substantially. The lead blocks are then placed above the patient supported in the beam on a transparent plastic tray, called the shadow tray. Table 13.1 gives the recommended lead shield thicknesses for various-quality beams.

Although the primary beam transmission can be reduced further by using extra thick blocks, the reduction in dose in the shielded region may not be that significant due to the predominance of scattered radiation from the adjoining open areas of the field.

Ideally, the blocks should be shaped or tapered so that their sides follow the geometric divergence of the beam. This minimizes the block transmission penumbra (partial transmission of the beam at the edges of the block). However, divergent blocks offer little advantage for beams with large geometric penumbra. For example, in the case of ⁶⁰Co, the sharpness of the beam cutoff at the block edge is not significantly improved by using divergent blocks. Also, for some clinical situations this sharpness is not critical or worth the time required for making divergent blocks, which have to be invariably custom designed for a given treatment setup. Therefore, most institutions keep a stock of straight-cut blocks of various shapes and dimensions. Divergent blocks are most suited for beams having small focal spots. Because the sides of these blocks follow beam divergence, one can reduce the lateral dimensions by designing the shields for smaller source to block distances without increasing the block transmission penumbra.

Although a number of systems have been used for field shaping (1,2,3,4,5,6,7,8), the one introduced by Powers et al. (1) is most commonly used in radiation therapy. This system uses a low melting point alloy, Lipowitz metal (brand name, Cerrobend), which has a density of 9.4 g/cm³ at 20°C (∼83% of lead density).
This material consists of 50.0% bismuth, 26.7% lead, 13.3% tin, and 10.0% cadmium (1). The main advantage of Cerrobend over lead is that it melts at about 70°C (compared with 327°C for lead) and, therefore, can be easily cast into any shape. At room temperature, it is harder than lead.

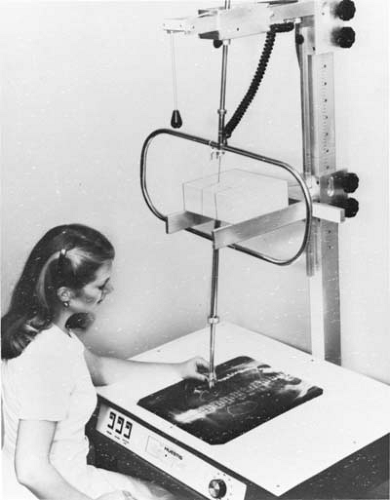
The minimum thickness of Cerrobend blocks required for blocking may be calculated from Table 13.1 using its density ratio relative to lead (e.g., multiply lead thickness by 1.21). In the megavoltage range of photon beams, the most commonly used thickness is 7.5 cm, which is equivalent to about 6 cm of pure lead. The procedure for constructing Cerrobend blocks starts with a simulator radiograph or a port film on which the radiotherapist draws the outline of the treatment field indicating areas to be shielded. The film is then used to construct divergent cavities in a Styrofoam block that are used to cast Cerrobend blocks. Figure 13.1 shows a Styrofoam-cutting device that consists of an electrically heated wire that pivots about a point simulating the source or the x-ray target. The film, the Styrofoam block, and the wire apparatus are so adjusted that the actual treatment geometry (same source to film and source to block distances) is obtained. The lower end of the wire traces the outline on the film.

If “positive” blocks such as lung blocks are to be made, cavities are cut in the Styrofoam with the heated segment of the wire and subsequently filled with melted Cerrobend. If a “negative” block with central area open and peripheral areas blocked is desired, an inner cut is first made to outline the field opening. An outer rectangular cut is then made to define the collimator field with a 1- to 2-cm margin. The three Styrofoam pieces thus made are placed on a Lucite plate and carefully aligned relative to the central axis. The intermediate piece, corresponding to the areas to be shielded, is then removed and Cerrobend is poured into the cavity.

It is important that the Cerrobend is poured slowly to prevent formation of air bubbles. Also, the Styrofoam block should be pressed tightly against a rubber pad at the bottom to avoid leakage of the liquid metal. The inside walls of the cavity may be sprayed with silicone for easy release of the Styrofoam pieces from the block.

The blocks can be mounted on a Lucite plate or blocking tray, which is premarked with the central axis cross-hairs. Blocks can also be placed on a template made on a clear film by tracing the outline of the field at the shadow tray position while the port film outline is placed at the distance at which the radiograph was taken.

Figure 13.2 shows examples of Cerrobend blocks, one constructed for shielding lungs and the other for a head and neck field.

Asymmetric fields are sometimes used to block off a part of the field without changing the position of the isocenter.

Although blocking is often used to generate irregular field shapes, rectangular blocking can be easily done by independently movable collimators, or jaws. This feature is very convenient when matching fields or beam splitting. In the latter case, the beam is blocked off at the central axis to remove divergence. Whereas half-beam blocks have been used as beam splitters in the past, this can now be done simply by moving in the independent jaws.

Most modern machines are equipped with independently movable jaws. Some machines have one independent jaw, others have two independent pairs, and some have all four jaws as independent. Operationally, the independent jaw option is interlocked to avoid errors in the setting of symmetric fields, in which case the opposite jaws open or close symmetrically. One of the effects of asymmetric collimation is the change in the physical penumbra (defined in) and the tilt of the isodose curves toward the blocked edge (Fig. 13.3). This effect is simply the result of blocking, which eliminates photon and electron scatter from the blocked portion of the field, thereby reducing the dose near the edge. The same effect would occur on the isodose curves if the blocking were done with a lead or Cerrobend block on a tray.

When asymmetric fields are used, special considerations must be given to the beam flatness and the dosimetric parameters used to calculate monitor units. Khan et al. (9) have proposed a system of dose calculation for fields generated by asymmetric collimators, which was discussed in Chapter 10.

A multileaf collimator (MLC) for photon beams consists of a large number of collimating blocks or leaves that can be driven automatically, independent of each other, to generate a field of any shape (Fig. 13.4). Typical MLC systems consist of 80 leaves (40 pairs) or more. The individual leaf has a width of 1 cm or less as projected at the isocenter. The leaves are made of tungsten alloy (ρ = 17.0–18.5 g/cm³) and have thickness along the beam direction ranging from 6 cm to 7.5 cm, depending on the type of accelerator. The leaf thickness is sufficient to provide primary x-ray transmission through the leaves of less than 2% (compared with about 1% for jaws and 3.5% for Cerrobend blocks). The interleaf (between sides) transmission is usually less than 3%. The primary
beam transmission may be further minimized by combining jaws with the MLC in shielding areas outside the MLC field opening.

Some MLC systems have double-focused leaves; that is, the leaves form a cone of irregular cross section diverging from the source position and move on a spherical shell centered at the source. The rationale behind a double-focused MLC is to provide a sharp beam cutoff at the edge. However, for high-energy beams this objective is achieved only to a limited extent, because the dose falloff at the edge is largely determined by scattered photons and electrons. Because double-focused MLCs are difficult to manufacture, some systems have been designed with rounded leaf edges
and directions of travel perpendicular to the central ray. The purpose of rounded edges is to provide constant beam transmission through a leaf edge, regardless of its position in the field.

An important consideration in the use of MLCs for stationary fields is the conformity between the planned field boundary, which is continuous, and the jagged stepwise boundary created by the MLC. The degree of conformity between the two depends not only on the projected leaf width, but also on the shape of the target volume and the angle of rotation of the collimator. Optimization of MLC rotation and setting has been discussed by Brahme (10). His analysis shows that the best orientation of the collimator is when the direction of motion of the leaves is parallel with the direction in which the target volume has the smallest cross section.

The physical penumbra (section 11.1) with MLC is larger than that produced by the collimator jaws or the Cerrobend blocks (Fig. 13.5). This is usually not a serious drawback except for the treatment of small fields or when blocking is required close to critical structures. Also, jaggedness of the field edges makes it difficult to match adjacent fields.

The use of MLC in blocking and field shaping is ideally suited for treatments requiring large numbers of multiple fields because of automation of the procedure, thus resulting in a significant reduction of setup time. MLC can practically eliminate the use of Cerrobend blocking except for shaping small fields or “island” blocking in which an area within the open portion of the fields needs to be blocked.

The importance of MLC is not just the replacement of Cerrobend blocking. The greater impact of this technology is in the automation of field shaping and modulation of beam intensity. Modern radiotherapy techniques such as 3-D conformal radiation therapy (Chapter 19) and intensity-modulated radiation therapy (Chapter 20) are dependent on the dynamically controlled MLC. Other applications include dynamic wedges and electronic compensation. For further details on MLC designs and applications, the reader is referred to a review by Boyer (11).

Surface dose is the result of electron contamination of the incident beam as well as the backscattered radiation (both electrons and photons) from the medium. It is well known that all x-ray and γ-ray beams used in radiation therapy are contaminated with secondary electrons. These electrons arise from photon interactions in the air, in the collimator, and in any other scattering material in the path of the beam. If a shadow tray is used to support beam-shaping blocks, secondary electrons produced by photon interactions in the tray and the air column between the tray and the skin surface significantly increase skin dose. The shadow tray is usually thick enough to absorb most of the electrons incident on the tray.

There has been a controversy as to the relative contribution of secondary electrons versus low-energy scattered photons to the dose in the buildup region. It is well known that as the field size increases, the depth dose in the buildup region increases, resulting in a shift in the depth of maximum dose, δ_max, to increasingly shallower depths (12,13,14). Specifically, the cause of the δ_max shift with field size has been studied by several investigators (15,16,17). Current evidence favors the hypothesis that the effect is predominantly caused by the secondary electrons.

Because of the steep dose gradient in the buildup region, the size of the dosimeter along the beam direction should be as small as possible. Extrapolation chambers (see Chapter 6) are the instruments of choice for these measurements. However, few institutions have these instruments available. Instead, fixed-separation plane-parallel ionization chambers are most commonly used for this purpose. Although these chambers are very suitable for measurements in regions of severe dose gradients, their response is dependent, in a complex manner, on their design. Several papers have discussed the inaccuracies in the measurement of dose in the buildup region when using fixed-separation plane-parallel chambers. These inaccuracies arise primarily as a result of electron scattering from the side walls of the chamber (18,19,20). These may be minimized by using a smaller plate separation and wider guard ring in the design of the chamber. Furthermore, the chambers may exhibit a significant polarity effect in the buildup region, which may be corrected by averaging the readings obtained with the positive and negative polarities. Gerbi and Khan (21) have studied several commercially available plane-parallel chambers and found that they overrespond in the buildup region. The errors were more severe at the surface and for the lower beam energies (e.g., ⁶⁰Co). The magnitude of overresponse at the surface for a ⁶⁰Co beam ranged from 9% to 20% for the chambers studied.

Thin layers (<0.5 mm) of thermoluminescent dosimeter (TLD) material can also be used for measuring dose distribution in the buildup region. The TLD phosphor (e.g., LiF) can be in the form of chips, crystals embedded in plastic, or powder layers (18,22,23). The surface dose may be obtained by extrapolating the depth dose distribution curve to zero depth. In vivo measurements of surface dose can also be made by placing thin TLD chips directly on the skin surface. Such measurements are useful in checking dosimetry if an unacceptable degree of skin reaction develops.

Studies have shown that the dose distribution in the buildup region depends on many variables such as beam energy, source to surface distance (SSD), field size, and configuration of secondary blocking tray (18,22,23,24,25,26). Table 13.2 gives values for different energies. These data are presented here as an example and should not be considered universal for all machines, especially for depths less than 2 mm. Reasonable agreement between different machines has been shown to exist for greater depths.

Examination of Table 13.2 would also indicate that for all energies the dose increases rapidly within the first few millimeters and then gradually achieves its maximum value at the depth of peak dose. For example, in the case of 4 MV, the percent depth dose increases from 14% to 74% in the first 2 mm, reaches 94% at a 5-mm depth, and achieves its maximum value at a 10-mm depth. A practical application of this phenomenon is the case in which buildup bolus (Chapter 12) is used
intentionally to maximize the dose on the skin (e.g., covering a scar with a strip of bolus). A tissue-equivalent bolus of 5 to 6 mm of thickness is usually adequate for 4 MV. Thus, the thickness of bolus required to achieve 90% to 95% buildup of dose is substantially less than the depth of maximum dose.