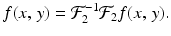(1)
Department of Mathematics and Statistics, Villanova University, Villanova, PA, USA
The ideas discussed in this chapter involve interactions between three transforms — the Radon transform, the Fourier transform, and the back-projection transform. Each of these transforms is defined in terms of improper integrals on infinite intervals. This raises the somewhat technical matter of determining which functions may appropriately be considered, an issue that is addressed in Appendix A. For the time being, we assume that any function being considered here meets the requirements. For those functions that arise in the practical world of medical imaging this is certainly the case.
6.1 The central slice theorem
The interaction between the Fourier transform and the Radon transform is expressed in an equation known as the central slice theorem (also called the central projection theorem).
In this presentation, the symbols 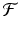 and
and 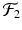 are used to denote the 1- and 2-dimensional Fourier transforms, respectively. The Radon transform is denoted by
are used to denote the 1- and 2-dimensional Fourier transforms, respectively. The Radon transform is denoted by 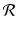 . The function f, representing, say, an X-ray attenuation coefficient, is a function of 2-dimensional Cartesian coordinates.
. The function f, representing, say, an X-ray attenuation coefficient, is a function of 2-dimensional Cartesian coordinates.
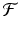 and
and 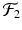 are used to denote the 1- and 2-dimensional Fourier transforms, respectively. The Radon transform is denoted by
are used to denote the 1- and 2-dimensional Fourier transforms, respectively. The Radon transform is denoted by 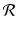 . The function f, representing, say, an X-ray attenuation coefficient, is a function of 2-dimensional Cartesian coordinates.
. The function f, representing, say, an X-ray attenuation coefficient, is a function of 2-dimensional Cartesian coordinates.Theorem 6.1.
Central slice theorem. For any suitable function f defined in the plane and all real numbers S and θ,
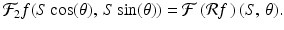
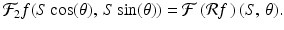
(6.1)
Proof.
Given f defined in the plane and real numbers S and θ, the definition of the 2-dimensional Fourier transform gives
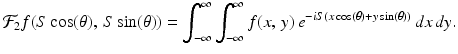
Now, instead of integrating separately over −∞ < x < ∞ and −∞ < y < ∞, we can reorganize the points in the xy-plane according to the value of xcos(θ) + ysin(θ). Specifically, for each real number t, gather together all of the points (x, y) in the plane for which xcos(θ) + ysin(θ) = t. This is exactly the line ℓ t, θ ! From our earlier analysis, we know that, for each point (x, y) on ℓ t, θ , the real number s = −xsin(θ) + ycos(θ) satisfies x = tcos(θ) − ssin(θ) and y = tsin(θ) + scos(θ). Moreover, the matrix ![$$\left [\begin{array}{cc} \partial x/\partial t&\partial x/\partial s\\ \partial y/\partial t & \partial y/\partial s \\ \end{array} \right ]$$](/wp-content/uploads/2016/10/A183987_2_En_6_Chapter_IEq4.gif) has determinant 1, so that ds dt = dx dy when the change of variables is put in place. With these changes, the right-hand side of (6.2) becomes
has determinant 1, so that ds dt = dx dy when the change of variables is put in place. With these changes, the right-hand side of (6.2) becomes
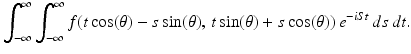
The factor e −iSt in the integrand of (6.3) does not depend on s, so it may be factored out of the inner integral. Thus, (6.3) becomes
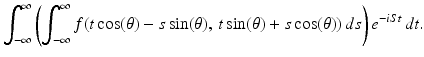
The inner integral in (6.4) is exactly the definition of 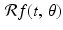 , the Radon transform of the function f evaluated at the point (t, θ). That is, (6.4) is the same as
, the Radon transform of the function f evaluated at the point (t, θ). That is, (6.4) is the same as
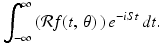
Finally, the integral (6.5) is the definition of the Fourier transform of 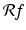 evaluated at (S, θ). That is, (6.5) is equal to
evaluated at (S, θ). That is, (6.5) is equal to
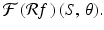
We have established, as we set out to do, the equality
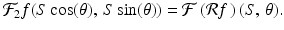
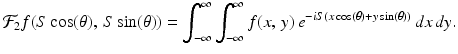
(6.2)
![$$\left [\begin{array}{cc} \partial x/\partial t&\partial x/\partial s\\ \partial y/\partial t & \partial y/\partial s \\ \end{array} \right ]$$](/wp-content/uploads/2016/10/A183987_2_En_6_Chapter_IEq4.gif) has determinant 1, so that ds dt = dx dy when the change of variables is put in place. With these changes, the right-hand side of (6.2) becomes
has determinant 1, so that ds dt = dx dy when the change of variables is put in place. With these changes, the right-hand side of (6.2) becomes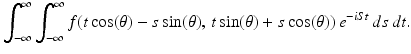
(6.3)
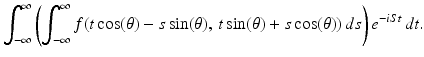
(6.4)
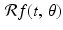 , the Radon transform of the function f evaluated at the point (t, θ). That is, (6.4) is the same as
, the Radon transform of the function f evaluated at the point (t, θ). That is, (6.4) is the same as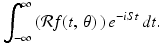
(6.5)
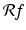 evaluated at (S, θ). That is, (6.5) is equal to
evaluated at (S, θ). That is, (6.5) is equal to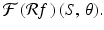
(6.6)
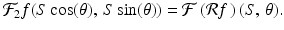
(6.7)
6.2 Filtered back projection
The back projection served as a first attempt at inverting the Radon transform and recovering the X-ray attenuation-coefficient function. The result was not the original function but a smoothed-out version of it. The next theorem, called the filtered back-projection formula, shows how to correct for the smoothing effect and recover the original function.
Theorem 6.2.
The filtered back-projection formula. For a suitable function f defined in the plane and real numbers x and y,
![$$\displaystyle{ f(x,\,y) = \frac{1} {2}\mathcal{B}\left \{\mathcal{F}^{-1}\left [\,\vert S\vert \,\mathcal{F}\left (\mathcal{R}f\,\right )(S,\,\theta )\right ]\right \}(x,\,y). }$$](/wp-content/uploads/2016/10/A183987_2_En_6_Chapter_Equ8.gif)
![$$\displaystyle{ f(x,\,y) = \frac{1} {2}\mathcal{B}\left \{\mathcal{F}^{-1}\left [\,\vert S\vert \,\mathcal{F}\left (\mathcal{R}f\,\right )(S,\,\theta )\right ]\right \}(x,\,y). }$$](/wp-content/uploads/2016/10/A183987_2_En_6_Chapter_Equ8.gif)
(6.8)
Proof.
The (2-dimensional) Fourier transform and its inverse transform are just that — inverses. Hence, for any suitable function f and any point (x, y) in the plane, we get