Clinical Safety

To state common intensity descriptors.

To identify the three interactions by which ultrasound may cause damage.

To understand the indication of risk quantified by the thermal index and the mechanical index.

To apply the principle of ALARA during sonography.

KEY TERMS

Cavitation

Duty factor

Intensity

Mechanical index

Power

Pulse average

Pulse repetition period

Spatial average

Spatial peak

Temporal average

Temporal peak

Thermal index

MEASUREMENT OF INTENSITY

Intensity is the physical parameter that describes the rate at which energy is conveyed by ultrasound through a small area. Each point within the ultrasonic field has an instantaneous intensity that varies with time (as the wave passes through the region). The potential for biological effects is associated with intensity. High-intensity ultrasound, causing extensive mechanical distortion, is considered more disruptive to living systems than low-intensity ultrasound. Intensity, by quantifying the temporal and spatial distribution of acoustic energy, provides the most complete description of exposure. A closely related parameter is power, which is the rate of total energy transmission and equals the collected intensity summed over the cross-sectional area of the beam. Traditionally, power is expressed in units of milliwatts (mW) and acoustic intensity in watts per centimeter squared (W/cm²) or milliwatts per centimeter squared (mW/cm²).

By placing the transducer in contact with the patient during scanning, acoustic energy is transmitted into tissue. Scanners operate in five different modes—B-mode, M-mode, continuous-wave Doppler, pulsed-wave (PW) Doppler, and Doppler imaging—in which the acoustic output varies over a large range. The highest power is exhibited in color flow imaging and pulsed wave Doppler. Power levels for the same type of device among manufacturers can differ considerably. During linear propagation, frequency, wavelength, and acoustic velocity of an ultrasonic beam are not affected by a change in intensity. However, for high-intensity applications, such as tissue harmonic imaging, propagation is nonlinear and the sinusoidal wave becomes distorted.

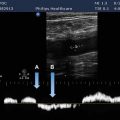
Peak negative pressure of a pulsed wave is an important parameter in the consideration of potential damage. The peak negative pressure is also called the peak rarefactional pressure (Figure 10-1). Ultrasound instruments produce peak pressure amplitudes ranging from 0.5 to 5.5 megapascals (more than 50 times greater than atmospheric pressure).

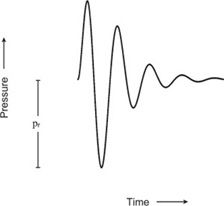
FIGURE 10-1. Pressure variation of a pulsed wave. The peak rarefactional pressure is designated p_r.

Intensity is proportional to the square of the acoustic pressure. The instantaneous intensity is calculated from the measurement of acoustic pressure in which the acoustic velocity and the density of the medium are known. Unfortunately, acoustic pressure in tissue cannot be measured directly. Typically, the transducer output is quantified using free-field conditions in which a hydrophone placed in water measures the acoustic pressure. The small physical dimension of the hydrophone (0.5–1 mm in diameter) samples a very small area to minimize spatial averaging. The ultrasound wave incident on the hydrophone induces a voltage via piezoelectric effect that is directly proportional to the acoustic pressure. Because the pressure is not constant but fluctuates as the wave passes a point in space, a time-varying waveform of the voltage and thus intensity is obtained. The spatial distribution of intensity is mapped by moving the hydrophone to different locations in the ultrasonic field. Since the attenuation rate for tissue is much greater than that for water, a correction factor (dependent on distance from the transducer) must be applied to convert the free-field intensity to the estimated intensity in tissue.

INTENSITY DESCRIPTORS

Scanning with a pulsed, focused ultrasound beam produces complex spatial and time-varying acoustic fields. Quantification of these patterns for all transducers is impractical and also this detailed information is extremely difficult to correlate with potential bioeffects. Thus, characterization of the ultrasonic field is accomplished by a few select parameters, usually related to energy, such as acoustic power, intensity, or peak negative pressure. The spatial and temporal dependence of the intensity are most often expressed in a simplified form by these shorthand descriptors.

Temporal Dependence

Large fluctuations of intensity are induced in the region through which the sound moves. Each pulsed wave consists of multiple cycles that produce intensity variations within the pulse itself—the maximum intensity designated temporal peak (TP), the intensity averaged over the duration of a single pulse designated pulse average (PA), and the intensity averaged over the longer interval of the pulse repetition period designated temporal average (TA). The pulse repetition period is the total time for one transmission-reception cycle, measured from the onset of one transmitted pulse to the onset of the next transmitted pulse. For a given pulse sequence temporal peak has the highest value, followed by pulse average, and finally by temporal average (Figure 10-2).

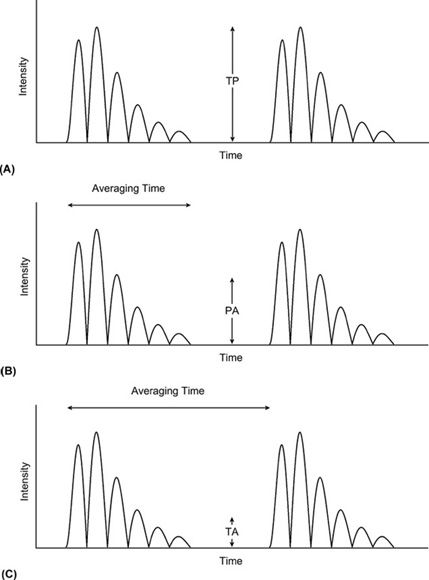
FIGURE 10-2. Specification of intensity with respect to time. (A) Temporal peak (TP). (B) Pulse average (PA). (C) Temporal average (TA).

The temporal-average intensity is considerably smaller than the pulse-average intensity. The ratio of pulse average to temporal average is the duty factor the fraction of time the transducer is actively generating ultrasound energy. For example, if the pulse duration is 1 µs and the time between pulses is 1 ms, the duty factor is 0.001. The temporal-average intensity is 1000 times less than the pulse-average intensity. A determination of the temporal peak intensity from the pulse-average intensity requires knowledge of the pulse shape. Temporal peak intensity is typically greater than the pulse-average intensity by a factor of 2–10.

The following analogy may help illustrate the relationship between intensity peak and intensity averaging: Suppose a row of sand castles has been built along the seashore, as shown in Figure 10-3. Each castle corresponds to a single pulse. The distance between castles denotes the pulse repetition period. The height of the tallest point of a castle represents the temporal peak. If a castle is flattened so the sand is spread evenly over its base, the level of the sand will be lower than the original peak. This flattened area corresponds to the pulse average. If the sand is distributed over the space between castles, the height of the sand will be reduced further. This represents the temporal average.

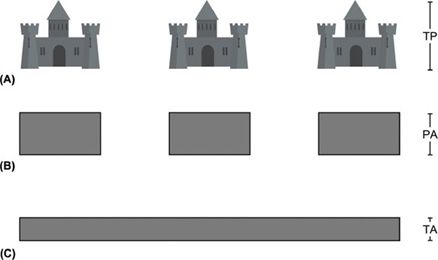
FIGURE 10-3. Temporal averaging. (A) The highest points on the sand castles (turrets) correspond to the temporal peak (TP). (B) Sand making up the turrets has been flattened and distributed across the base of each castle. This corresponds to the pulse average (PA). (C) The sand has been flattened to cover the area between the castles. This corresponds to the temporal average (TA).

Spatial Dependence

The additional factor of space is now considered in the shorthand description of intensity. Once more, the peak or average value with respect to the variable (in this case space) is analyzed. The temporal peak intensity, pulse-average intensity, or temporal-average intensity is mapped as a function of position within the ultrasonic field.

The maximum intensity of all measured values within the ultrasonic field is designated as the spatial peak (SP). Thus, three combinations are possible depending on which temporal intensity is evaluated:

I(SPTP)—Spatial peak, temporal peak intensity

I(SPPA)—Spatial peak, pulse-average intensity

I(SPTA)—Spatial peak, temporal-average intensity

where each intensity descriptor denoted by capital “I” includes a designation specifying how the acoustic field is characterized. The variation in intensity along the axis of propagation for a focused transducer is illustrated in Figure 10-4. The focusing of the transducer is the most important determinant of the location of the spatial peak.

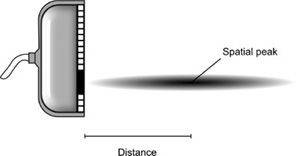
FIGURE 10-4. Intensity variation in the ultrasonic field for a focused transducer. The axial intensity is highest at a particular distance from the face of the transducer, which defines the location and magnitude of the spatial peak intensity.

Spatial averaging (SA) of the temporal intensity over the cross-sectional area of the beam is also a common representation (Figure 10-5). Again, three combinations are possible:

I(SATP)—Spatial average, temporal peak intensity

I(SAPA)—Spatial average, pulse-average intensity

I(SATA)—Spatial average, temporal-average intensity

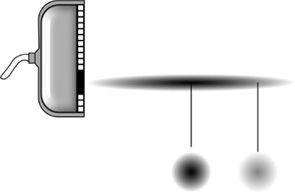
FIGURE 10-5. Relationship of spatial peak (SP) and spatial average (SA) intensities. The intensity variation across the width of the beam is shown for two points. The SA intensity is found by averaging the intensity over the beam cross-sectional area.

RISK

The widespread acceptance of ultrasound is attributed in large part to one especially attractive feature—ultrasound is not a type of ionizing radiation. Furthermore, no acute harmful effects have been reported following diagnostic ultrasound examinations. Nevertheless, when large populations are exposed to any agent, it is appropriate to investigate any potential long-term effects, which may not be evident on an individual case-by-case basis.

A risk (i.e., potential harmful effect) versus benefit (i.e., diagnostic information derived) analysis is necessary to assess medical efficacy. Quantification of risk from ultrasound examination is not currently available and will never be precisely known. The potential harmful effects to the exposed human population must be inferred from various investigational findings.

A threshold effect is one in which no adverse effect exists below a certain value of a given parameter (in this case, intensity) and above which an adverse and possibly irreversible effect is possible or likely. An illustration of a threshold effect would be the heating of an egg in a skillet. At room temperature the egg white exists as a clear, gelatinous substance. When the temperature of the skillet reaches a certain temperature (the threshold), the protein of the egg white is permanently denatured. In a biological system, intensity levels below a certain value may be incapable of inducing an effect if a threshold exists. For a biologic response with a threshold, adverse effects reported for high intensity are not present at intensity levels lower than the threshold. If the biologic response has no threshold, however, any exposure to the physical agent carries some risk; the question then becomes whether effects observed at high intensity can accurately predict the risk at low intensity based on theoretical models.

For the study of any potential effect, as the probability of that effect approaches zero, the number of individuals necessary to quantify this probability approaches infinity. In most situations, we attempt to avoid large risks and accept risks that may be nonzero but that are too small to measure accurately.

MECHANISMS OF BIOLOGIC DAMAGE

Three mechanisms by which ultrasound interacts with matter have been identified: acoustic radiation force, thermal, and cavitation. Cavitation and radiation force are often classified together as mechanical or nonthermal interactions.

Radiation Force

Radiation force describes damage caused by mechanical vibrations of tissue and generally includes all but thermal and cavitational effects. As the ultrasound wave propagates through the medium by interactions between neighboring particles, the particles undergo considerable changes in velocity and acceleration. An object with a density different from that of the surrounding medium experiences a force in the ultrasound field, because acoustic pressure is applied over its surface. This causes translational or rotational motion of the object. The rotational motion may give rise to acoustic streaming (i.e., circulatory flow of the fluid), and spinning of intracellular particles may be induced. At high intensities, high-velocity gradients are formed near solid boundaries. The resulting microstreaming (i.e., rapid movement of fluid in a localized area) can fragment the macromolecules in these regions. This generally occurs at intensity levels much greater than diagnostic ultrasound and is not of concern in clinical practice.

Thermal Interactions

As the ultrasound beam propagates through tissue, acoustic energy is converted into heat. The increased temperature has the potential to cause irreversible tissue damage. Time at elevated temperature necessary to elicit a response, particularly for the fetus, is well documented. The rate of temperature rise depends on the temporal-average intensity, the rate of absorption, the cross-sectional area of the beam, the duration of exposure, and the heat-transport processes (thermal conductivity and blood flow). Within the frequency range of 1–20 MHz, the rate of energy absorption increases with frequency. Thermal effects dominate at the low megahertz frequencies and tend to mask other (nonthermal) effects.

Cavitation

Regions of compression and rarefaction are created along the path of propagation. Tissue is subjected to increases and decreases in pressure in an alternating fashion, and these pressure fluctuations cause gas bubbles to exhibit dynamic behavior. The gas bubbles may preexist in tissue or may be formed by the wave action. This phenomenon is known as cavitation, which can be either stable or transient.

STABLE CAVITATION

In stable cavitation, microbubbles already present in the medium expand and contract during each cycle in response to the applied pressure. The bubbles may also grow as dissolved gas leaves the solution during the negative-pressure phase. Each bubble oscillates about the expanding radius for many cycles without collapsing completely. At a specific frequency of sound, dependent on the microbubble size, the vibration amplitude is maximized.

The action of the gas bubble in the liquid is analogous to a child’s swinging on a swing. An external force (push) applied to the child at the proper instant in the oscillatory path increases the height of the swing. If the force is repeated over and over at the proper frequency, the motion of the swing is amplified. If the child is pushed opposite the direction of movement, the height of the swing decreases. The interplay between the rate of pushing and the physical characteristic of the swing (e.g., length of rope between the pivot point and the seat) is essential for maximum effect. Similarly, in cavitation, the interaction between the size of the gas bubble and the frequency becomes critically important.

A free air bubble in water undergoes resonance at 1 MHz when its radius is 3.5 microns. At higher frequencies, the size of the bubble required for resonance decreases. Bubbles somewhat smaller than resonance size tend to grow, whereas those significantly larger than resonance size do not sustain stable cavitation. Oscillations of a gas bubble may produce high shearing forces in the nearby surrounding areas. Stable cavitation may also give rise to microstreaming. The radial oscillatory motion of the bubble is not always spherically symmetrical. An adjoining solid boundary may distort the motion of the bubble and cause eddies near the gas-liquid interface. High-velocity gradients are created in the localized region of the oscillatory boundary layer. Biomolecules or membranes subjected to such gradients can fragment or rupture.