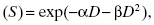- Describe the biological principles of radiation cancer treatments
- Differentiate between external beam and internal radiation therapy
- Describe the techniques and equipment used to perform radiation oncology treatments
- Describe some of the side effects of radiation therapy
This chapter on radiation treatment of cancer is included in a book on the biological effects of medical imaging because inevitably, the reader will be considered an expert or at least knowledgeable in all things concerning radiation. Half of all cancer patients receive radiation therapy at some point in their course of the disease. It is likely that the reader or their friends and family will ask about someone who has, is, or will be receiving radiation therapy treatments. This chapter covers the basics of the biology, equipment, and complications of radiation therapy so the reader can answer some basic questions regarding radiation treatment of cancer.
Radiation therapy, also called radiation oncology, surgery, and chemotherapy are the three primary methods to eradicate cancer. Both surgery and radiation therapy are local control procedures. They treat cancer either by cutting it completely out or killing “all” the cells in the treatment volume. Chemotherapy is a systemic treatment that aims to kill all the cancer cells distributed throughout the body. All three modes of treatment attempt to kill the cancer cells without too much damage to normal cells.
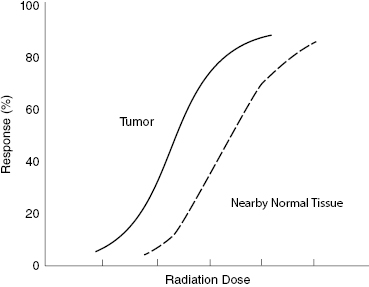
Within a year of Wilhelm Roentgen’s discovery of X-rays, reports were published on the use of X-rays to treat skin cancer. For over 100 years, physicians have been studying the effects of radiation on normal and cancerous tissues. Radiation damages all cell components, but damage to the tumor cell’s DNA can prevent reproduction and halt cancer growth. Radiation therapy treatments are designed to maximize damage to tumor cells while restricting damage to the surrounding normal tissues to a tolerable level. Figure 11.1 presents a comparison of the dose–response of tumor cells and nearby normal tissues. Notice that the response of normal tissue rises above a few percent before the tumor response reaches 50%. This means that some normal tissue damage is inevitable in all radiation therapy treatment. In most cases, the normal tissue damage is tolerable and illustrates the difficulty in balancing tumor killing against normal tissue damage.
Figure 11.1 Tumor and normal tissue dose–response curves showing that normal tissue response occurs at higher doses than tumor response but that high tumor response inevitably involves some normal tissue response.
Early studies quickly established that rapidly dividing tissues are more sensitive to radiation than tissues with cells that divide more slowly. They also showed that a series of fractionated doses killed more cancer cells than the same dose delivered in a single exposure. The explanation was that several fractions of the total dose over time allowed normal cells to recover whereas the tumor cells did not recover from the radiation as quickly.
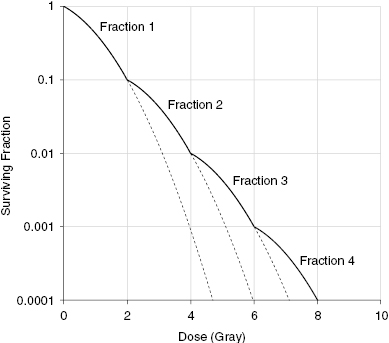
Figure 11.2 shows a schematic representation of a fractionated versus single-dose cell survival curve experiment. Notice the higher survival of cells exposed to a series of fractionated doses compared with those receiving a single dose. This allows normal tissue cells to survive or recover from the radiation dose.
Figure 11.2 Representative cell survival curves showing the effect of fractionation. Cells exposed to the same total dose divided into two reactions show a greater survival than the cells receiving a single dose.
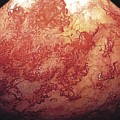
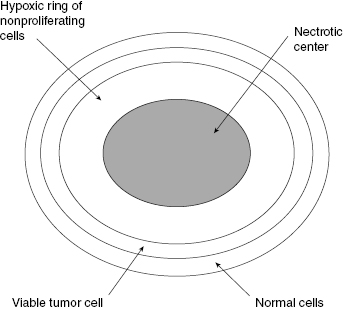
Observations of in vivo tumors showed that many solid tumors have a necrotic central portion surrounded by a ring of hypoxic cells that are not proliferating but are still viable if reoxygenated. Figure 11.3 shows an idealized sketch of such a tumor with a necrotic center, a ring of hypoxic cells surrounded by oxygenated viable tumor cells. Actual tumors are not all perfectly spherical, but Fig. 11.3 is drawn to emphasize the important points of the anoxic (without oxygen) necrotic center and the hypoxic (lower than normal) rim around the necrotic center. The oxygen diffusion distance is about 200 μ. Although most solid tumors have developed their own blood supply through angiogenesis, they still “piggyback” on the existing blood vessels to obtain oxygen and nutrients.
Figure 11.3 A schematic view of a spherical tumor showing a hypoxic necrotic center surrounded by a ring of hypoxic, radioresistant tumor cells and an outer ring of oxygenated tumor cells.
The Four Rs of Radiation Oncology
To explain the observations following fractionation experiments and treatments, radiation biologists developed the four Rs of radiation therapy or radiation biology. Table 11.1 lists these four observations.
Repair is the process of rejoining DNA strands. Most repairs occur within 15 minutes to 1 hour. Split-dose experiments show that repair is completed within about 6 hours.
Redistribution refers to the change in the fraction of cells in each phase of the cell cycle. Cells in different parts of the reproductive cycle have different sensitivities. M is the most sensitive, and late S is the least sensitive. Radiation exposure kills more of the cells in the M phase, and more cells in the S phase survive. This effect has not been shown to be advantageous in radiation therapy.
Reoxygenation occurs as the sensitive, well-oxygenated tumor cells are killed and the tumor shrinks. The outer layers die, and anoxic cells are reintroduced to oxygen. Reoxygenation does not affect treatments with high linear energy transfer (LET) radiation because the higher-density radiation tracks kill hypoxic tumor cells as well as well-oxygenated tumor cells.
Repopulation of the clonogenic cells occurs during the course of fractionated radiation therapy. Each radiation fraction reduces the total tumor population while repopulation rebuilds it. The desired effect is a reduction in the total tumor population. Repopulation of the tumor may occur because the vascularity of the tumor increases as the tumor shrinks. Reoxygenation may counteract the effect of repopulation.
Cell Survival Curves and Fractionation
Models have been developed to reproduce the curved portion of the cell survival curve. One of the more popular models is the linear–quadratic or LQ model. In the LQ model, the survival S after a dose of D is given in Equation 11.1:
where α represents the linear portion of the survival curve and β represents the quadratic portion of the survival curve. Tissues with higher mitotic indices are classified as “early responders” or more radiosensitive and tend to have higher α/β ratios.
The LQ or α/β model shown in Equation 11.1 fits the curved portion of the survival curve up to doses of 5–6 Gy, which includes the doses used in radiation therapy.
Figure 11.4 shows how the LQ model fits the lower-dose curved portion of the cell survival curve, which is the dose range used in radiation therapy treatments.