2 Physics and Artifacts
Ultrasound imaging is a popular imaging technique in clinical practice. It has been used for over 6 decades. Medical ultrasound is relatively inexpensive, noninvasive, and portable; it has good spatial and temporal resolution; and it is safe. Ultrasound imaging is based on the use of the echo of a sound wave to produce an image of the insonated area. It is derived from techniques like SONAR (sound navigation ranging) and nondestructive material testing.
The first clinical ultrasound image was produced by Karl and Friedrich Dussik in Vienna in 1946. They used a transmission technique, similar to the technique used in X-ray imaging. In 1949, the first pulse echo was described. After that, 2D gray-scale images were produced. In 1956, Ziro Kaneko introduced the Doppler technique. In 1965, Siemens introduced the VIDOSON, the first real-time 2D gray-scale system.
In 1971, the first commercially available array transducer–based systems were introduced simultaneously by Professor Klaas Bom of Erasmus University in Rotterdam, the Netherlands (the Multiscan system) and by Toshiba (the SSD-12). In 1979, Professor Bom in conjunction with Professor Wladimiroff, an obstetrician, introduced the Minivisor, the first portable ultrasound imager.
After these advances, ultrasound scanners were made available by many companies. The techniques evolved into applications like life 3D and elastography, and the developments are still going fast.
2.1 Basic Principles of Ultrasound
2.1.1 Ultrasonic Waves
Ultrasound is defined as sound having a frequency higher than 20 kHz. This is beyond the upper limit of the human audible spectrum. Frequencies used in medical ultrasound typically range from 1 to more than 20 MHz.
Ultrasonic waves are longitudinal compression waves. Longitudinal means that the movement of the particles of the medium is parallel to the direction of the wave movement. This is a contrast to transverse waves, like waves on water. Here, the movement of the particles is perpendicular to the direction of the wave. In longitudinal pressure waves, the movement of the particles leads to regions of compression and expansion corresponding to high- and low-pressure areas, respectively.
2.1.2 Wave Propagation in Homogeneous Media
The degree of compression is related to properties of the propagation medium. These properties are characterized by the acoustic impedance, Z
with ρ being the density of the medium [kg·m–3] and c being the speed of sound in the medium [ms–1]. Table 2.1 lists various properties of materials and tissues.
Material/Tissue | ρρ{\rho } [kg·m–3] | c [ms–1] | Z [kg·m–2·s–1] (× 106) |
Air | 1.2 | 330 | 0.0004 |
Lung | 300 | 600 | 0.18 |
Fat | 924 | 1,450 | 1.34 |
Water | 1,000 | 1,480 | 1.45 |
Kidney | 1,041 | 1,565 | 1.63 |
Blood | 1,058 | 1,560 | 1.65 |
Liver | 1,061 | 1,555 | 1.65 |
Muscle | 1,068 | 1,600 | 1.71 |
Skull bone | 7,500 | 4,080 | 30.6 |
The frequency (f) of the ultrasonic wave is unaffected by the propagation medium. The wavelength (λ), however, is affected related to the medium by the following equation:
2.1.3 Wave Propagation in Inhomogeneous Media
Just like visual light, sound breaks and reflects on discontinuities in media (Fig. 2.1), according to Snell’s law:
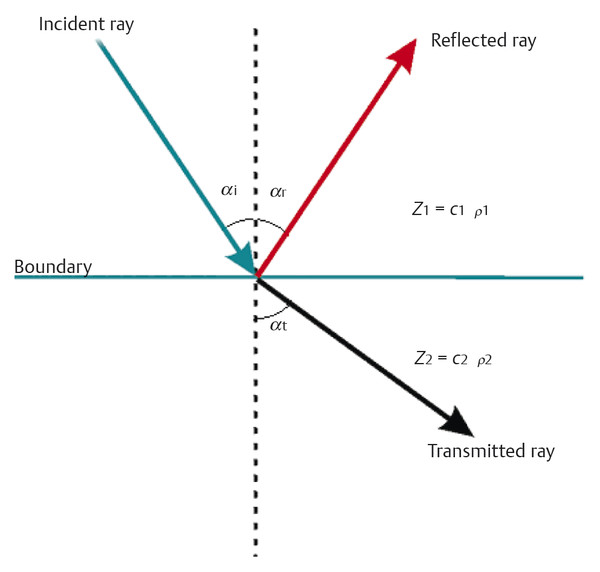
Reflection
The reflection coefficient Rp describes the fraction of sound pressure that is reflected on an interface and is given by the following equation:
with Pi and Pr representing the incident pressure amplitude (height) and the reflected pressure amplitude, respectively.
For a perpendicular incidence (α = 0°, cos α = 1), this formula simplifies as follows:
Intensity is the amount of power (energy per unit of time) per unit area. It is proportional to the square of the pressure amplitude:
In case of a perpendicular incidence, the intensity reflection coefficient thus becomes:
with Ii and Ir representing the incident intensity and the reflected intensity, respectively.
RI ranges between 0 and 1. At 0, no energy is reflected; no echo occurs. This is when Z1 = Z2. There is no discontinuity in the medium and no boundary to reflect on. At RI = 1, all energy in the incident wave is reflected. No energy is transmitted through the boundary. This occurs when there is a great difference between Z1 and Z2 (Z1 << Z2 or Z1 >> Z2).
As can be seen in Table 2.1, the acoustic impedance values of biomaterial are in the order of 1.3 to 1.7 × 106 kg·m–2·s–1. This leads to reflection coefficients in the order of 0.02. This means that 2% of the intensity of an incidence wave reflects on the boundary and 98% is transmitted and can produce echoes of adjacent structures. Note that without these small differences in the acoustic impedance of biomaterials, ultrasound imaging would not be possible.
Refraction
As seen in Fig. 2.1, the transmitted wave is refracted. An interesting phenomenon called total reflection occurs when, given c2 > c1, the angle of incidence αi gets beyond a critical value called αc. This angle is called the critical angle (Fig. 2.2). The refracted wave does not penetrate the second medium. It travels along the interface. Hence αt = 90°.
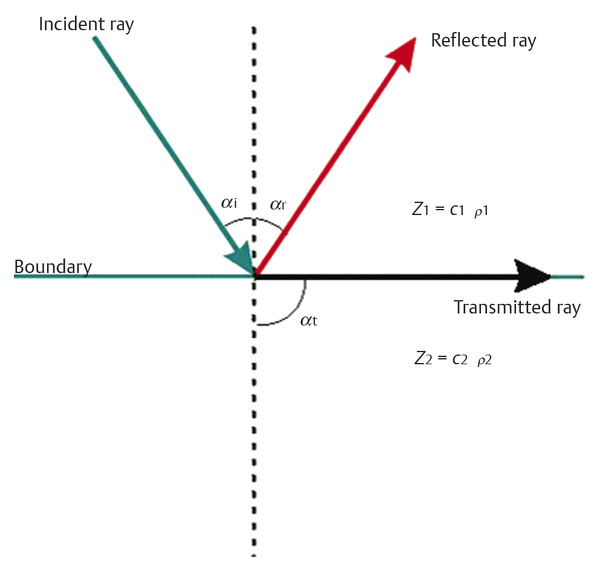
We get the critical angle αc by substitution of sin αt = 1 into Eq. 2.3:
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree